Do you want to know a secret?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
There’s a simple trick to finding the derivative of an inverse function!
But first, let’s talk about inverse functions in general.
Inverse Functions
An inverse function is any one-to-one function where it never takes on the same value twice (i.e., there is only one y-value for every x-value).
This means that every element in the codomain, in this case, the range, is the image of at most one element of its domain.
Additionally, as CoolMath points out, an inverse function passes the Vertical Line Test and the Horizontal Line Test, which stipulates that no horizontal line intersects its graph more than once; thus, no two elements in the domain correspond to the same element in the range.
And if we recall from Algebra, to find the inverse of a one-to-one function we:
- Write y=f(x).
- Switch x and y, and resolve for y.
Example
Let’s find the inverse function for f(x) and sketch both f(x) and its inverse on the same coordinate axis.

How To Find The Inverse Of A Function
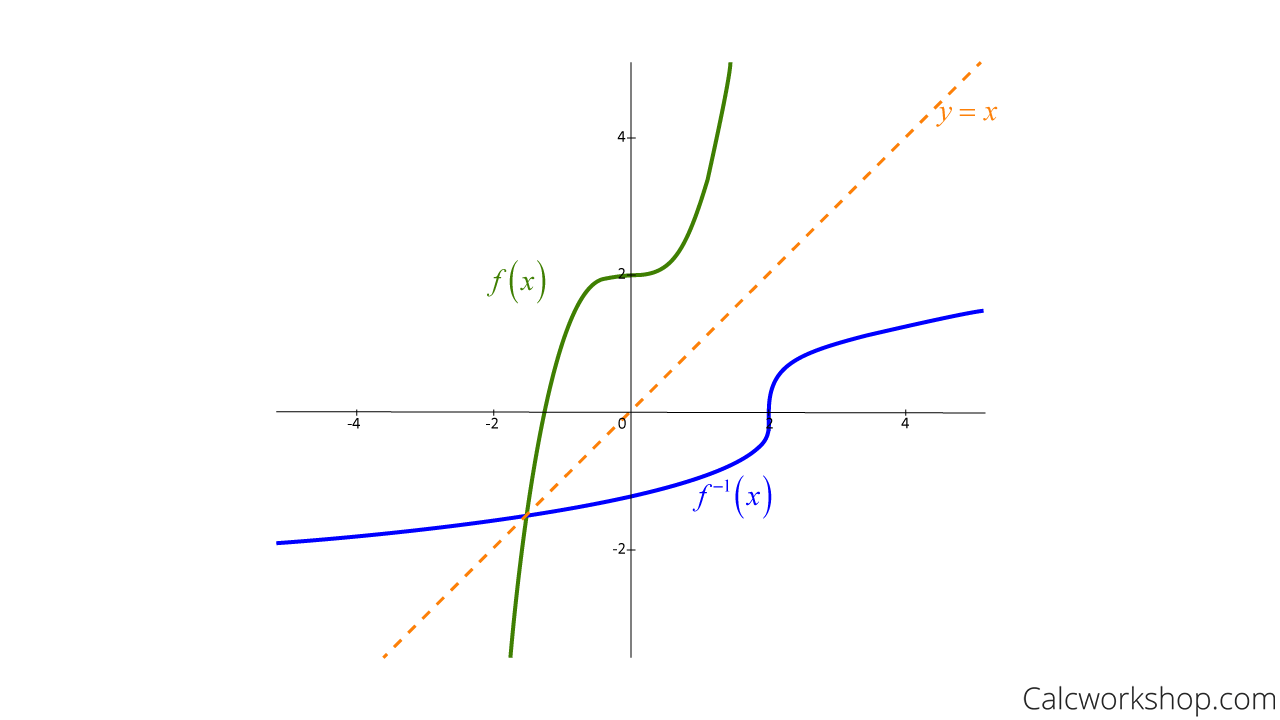
Graph Of Inverse Functions
So, an inverse function can be found by reflecting over the line y = x, by switching our x and y values and resolving for y.
And that is the secret to success for finding derivatives of inverses!
How To Find The Derivative Of An Inverse Function
If f(x) is a continuous one-to-one function defined on an interval, then its inverse is also continuous. Moreover, if f(x) is a differentiable function, then its inverse is also a differentiable function.
Formula
But the big key to using this formula is to know that you will be given the y-value (i.e., “a”), and it’s your job to first find the x-value (i.e., “b”).
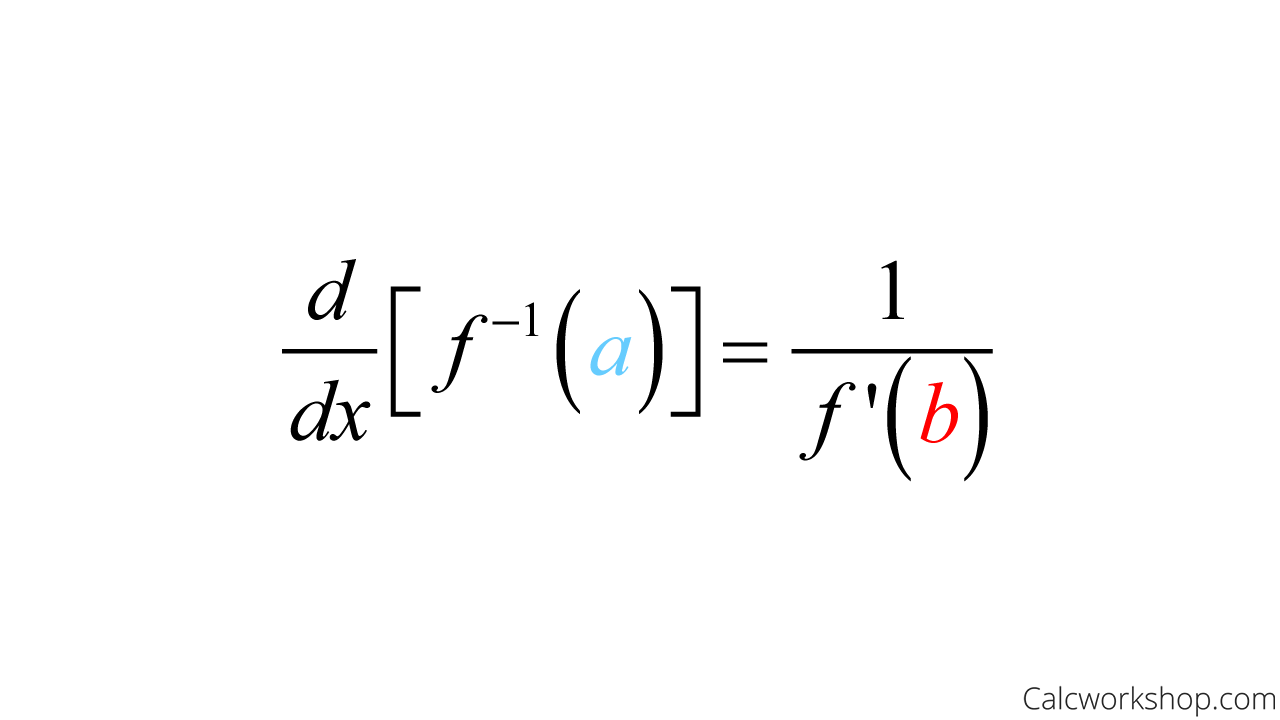
Inverse Derivative Formula
Sneaky!
Process
Okay, so here are the steps we will use to find the derivative of inverse functions:
- Know that “a” is the y-value, so set f(x) equal to a and solve for x. This value of x is our “b” value.
- Take the derivative of f(x) and substitute it into the formula as seen above.
- Plug our “b” value from step 1 into our formula from step 2 and simplify.
Example
While this may seem strange at first, the following example will highlight these steps and hopefully make sense of the procedure.
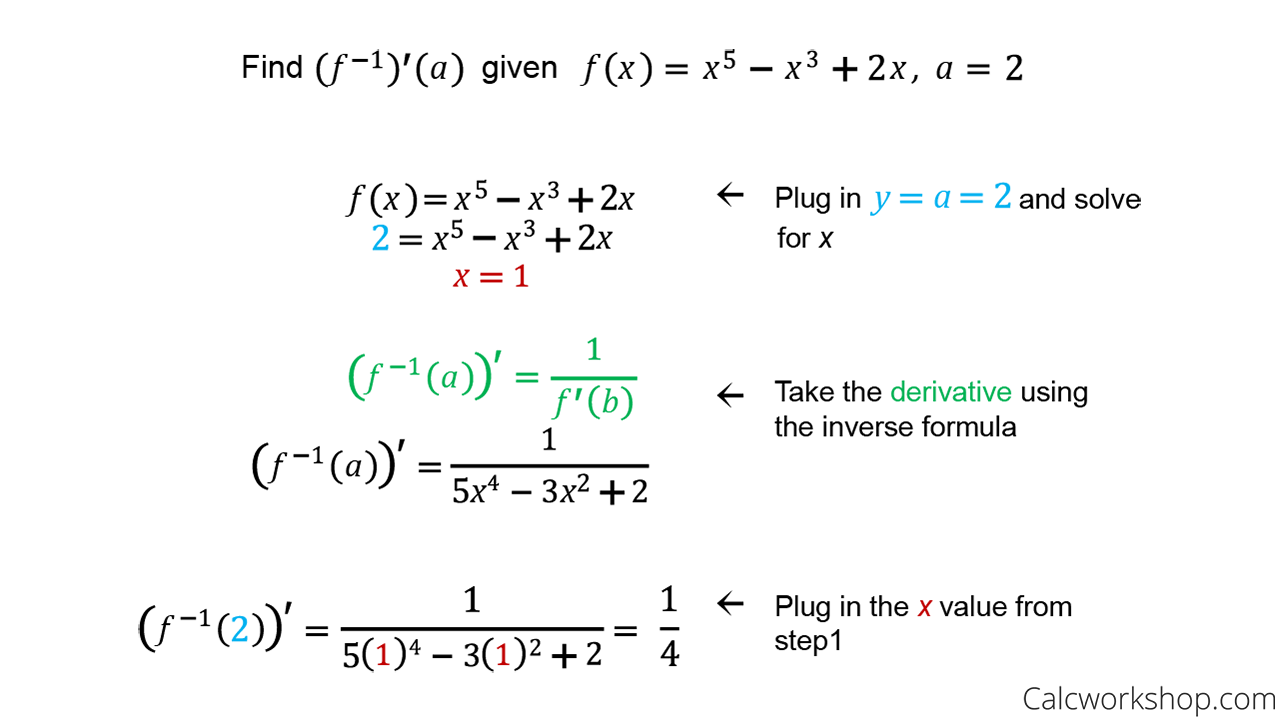
Find the Derivative of the Inverse
See, not so bad, right?
Summary
You will learn in this video that sometimes we will need to employ some of our algebra skills like factoring, quadratic formula, and possibly synthetic division to solve for our unknown “b” value, but don’t worry, I’ll make sure to remind you of all of these solving techniques and how to use them when applicable.
Together we will learn the explicit formula for finding the derivative of an inverse function and not be fooled or tricked by the question by walking through several examples.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.