Did you know that an M&M is a perfect illustration for understanding a composite function, which is the key to understanding the Chain Rule?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
What Is A Composite Function
Okay, so what is a composite function?
Simply put, a composite function is a function that is inside another function. In other words, one function comprises (encompasses) the other function.
As with most things, it’s easier to explain with a visual.
I want you to picture an M&M from Mars Incorporated, with its candy-coating shell and milk chocolate filling.

Chain Rule – M&M Analogy
The candy-coating shell represents the outer function, while the chocolate filling is the inner function.
This means the shell contains the chocolate, so it’s a perfect way to characterize a composite function.
But why do we care?
Because we desire to differentiate a function with two layers (i.e., one function inside of another), where each layer is equally important, just like with an M&M, the candy coating is just as delicious as the chocolate filling.
And just as both layers are equally important to the creation of the tasty treat, both layers of a composite function are essential as well.
So, this means that we need to focus on each layer, one at a time.
And here’s how we do that.
Chain Rule For Derivatives
Essentially, we have to melt away the candy shell to expose the chocolaty goodness.
Then we multiply by the derivative of the inside function.
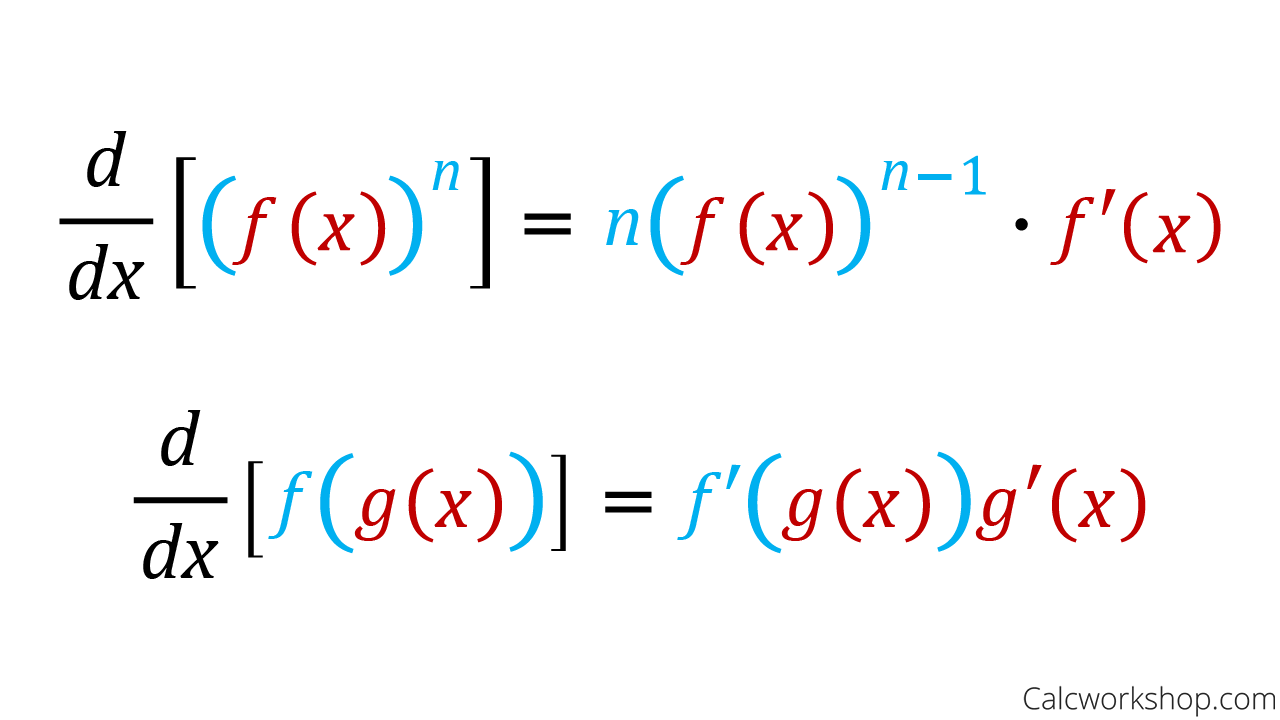
Understanding the Chain Rule
Formally, we express the chain rule for derivatives as follows:
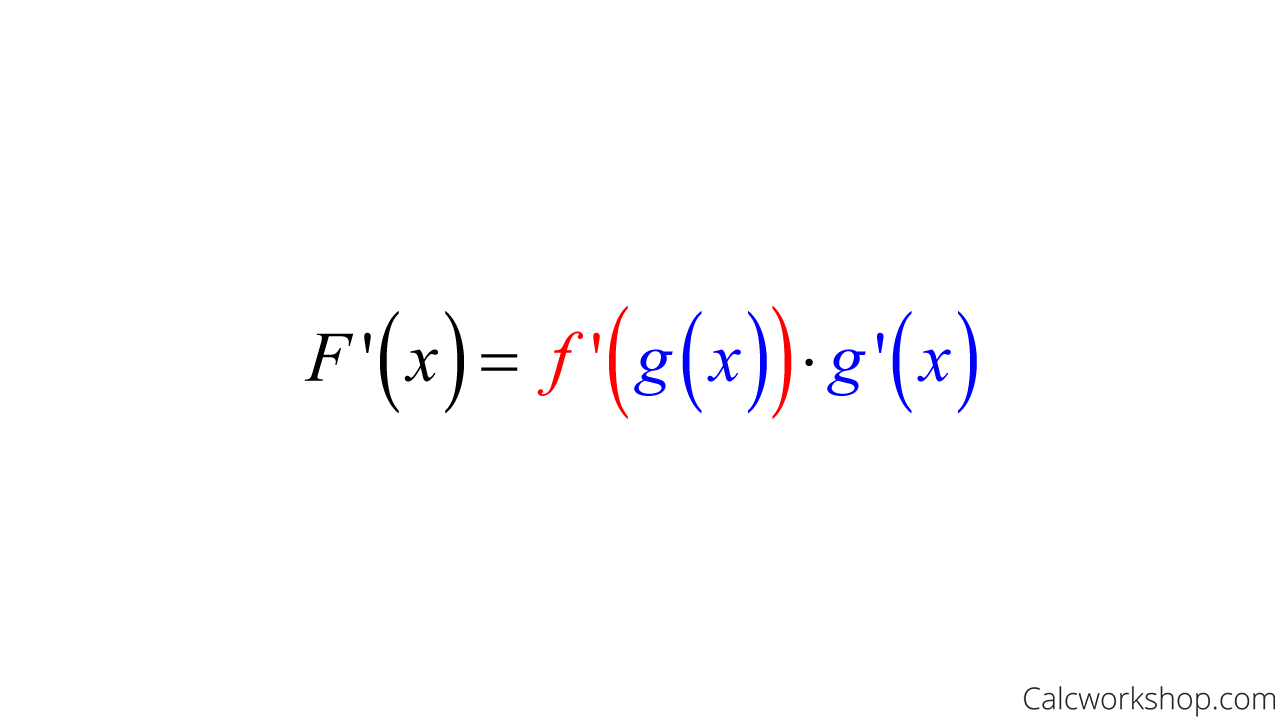
Derivative Of Composite Function — Formula
Worked Example
Let’s now take a look at a problem to see the chain rule in action as we find the derivative of the following function:
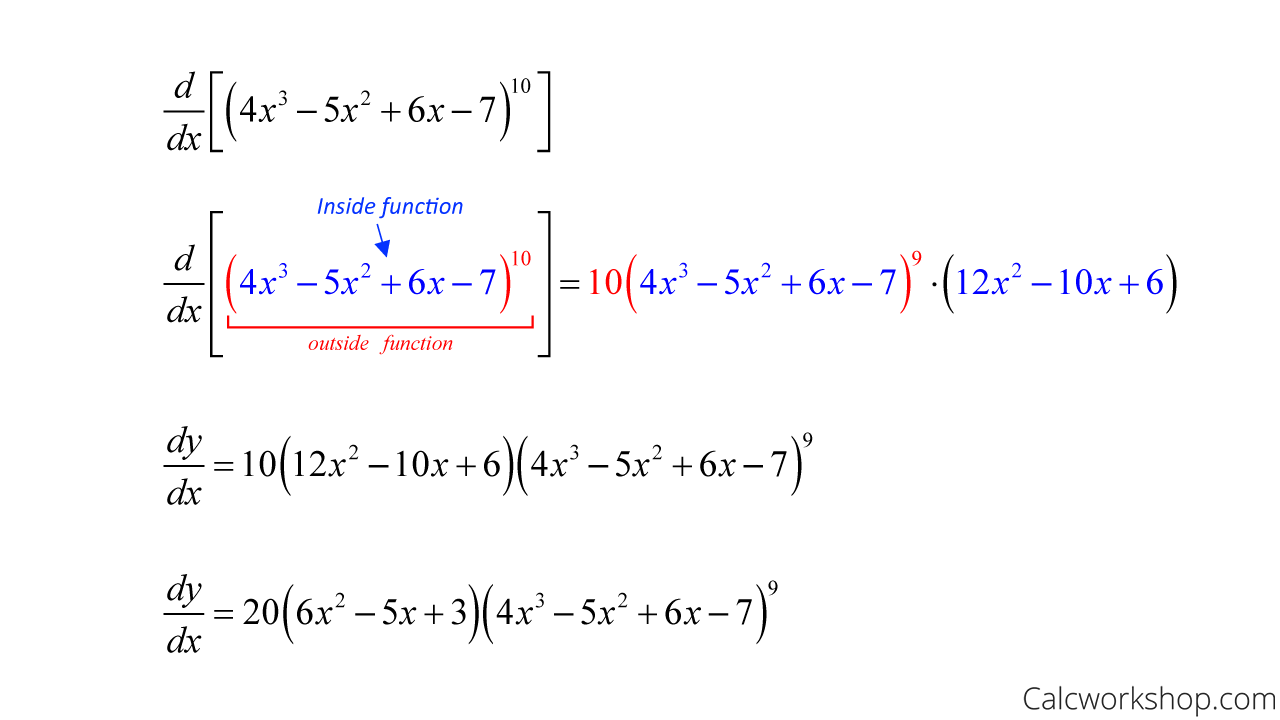
Chain Rule — Examples
See, all we did was first take the derivative of the outside function (parentheses), keeping the inside as is. Next, we multiplied by the derivative of the inside function, and lastly, we simplified.
Isn’t the chain rule superb!
Without it, we would have had to multiply the polynomial you see in blue by itself 10 times, simplify, and then use the power rule to find the derivative!
Good grief! That would have been painful.
Thanks to the chain rule, we can quickly and easily find the derivative of composite functions — and it’s actually considered one of the most useful differentiation rules in all of calculus.
In fact, we will come to see that the chain rule’s helpfulness extends beyond polynomial functions but is pivotal in how we differentiate:
- Trigonometric Functions
- Exponential Functions
- Logarithmic Functions
- And More
Wrapping Up
So, throughout this lesson, we will work through numerous examples of the chain rule, combining our previous differentiation rules such as the power rule, product rule, and quotient rule, so that you will become a chain-rule master!
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.