Rounding Decimals
Simple How-To w/ 27 Examples!

Did you know that rounding decimals is used all the time in our every day lives?

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Rounding, which is a way for us to approximate a numerical value, helps us deal with:

• Money
• Sports statistics
• Height and weight
• And even time

For example, rather than saying your 5 feet and 4 and three-quarters inches, we would round up and say we’re 5 feet 5 inches.

Or let’s assume the time is 2:01 pm, isn’t it just easier to round and say it’s 2 pm?

Decimal Rounding In Real Life

Yep! Rounding helps, and we use it all the time.

Rounding Rules

But to use it effectively, we have to know the steps. So, what are the rules for rounding decimals?

1. First, we need to locate the digit we wish to round. In other words, we will use our place value skills for finding the proper digit.
2. Next, we look to the number directly to its right. If it’s 0,1,2,3, or 4, we leave the number as it is, but if the number to the right is 5,6,7,8, or 9, we round up.
3. Lastly, we write our final answer, replacing all the numbers to the right of the digit we wish to round to with zeros.

Rules For Rounding

That’s it.

And, no matter if you’re rounding whole numbers or decimals, the rules are the same!

Worked Examples

Now let’s look at two examples for rounding decimals to the underlined value.

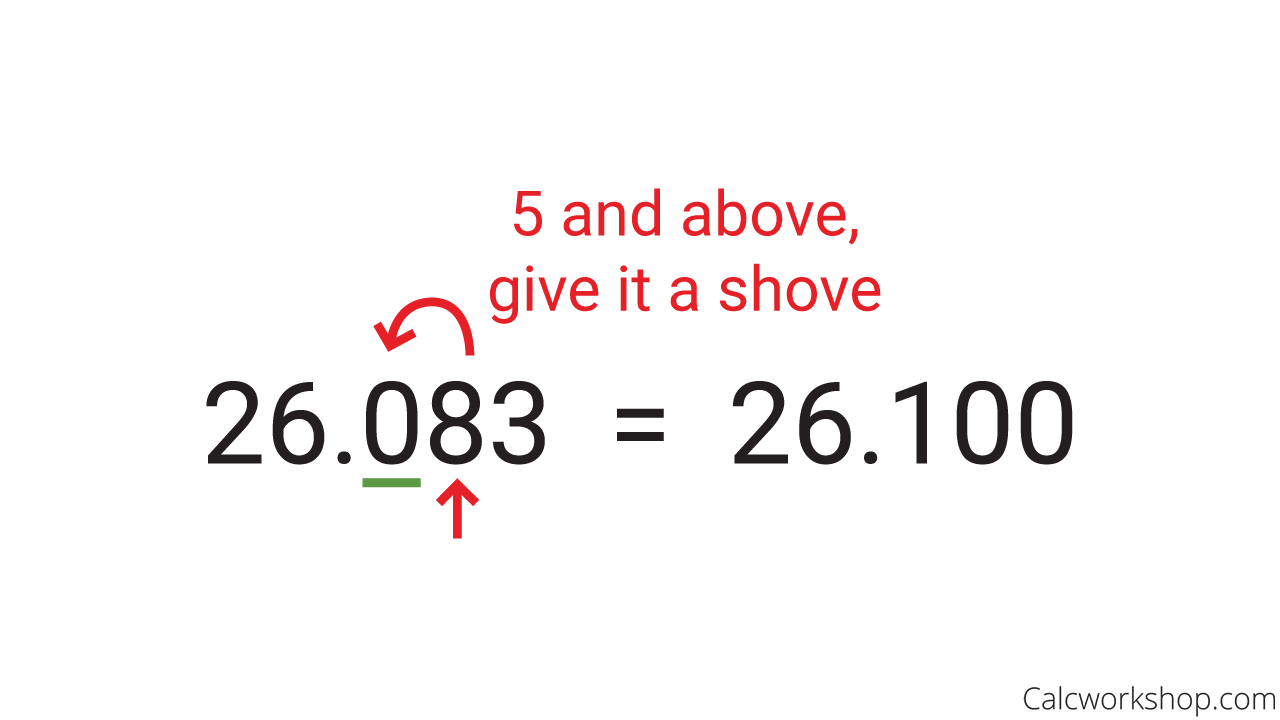
When To Round Up A Decimal

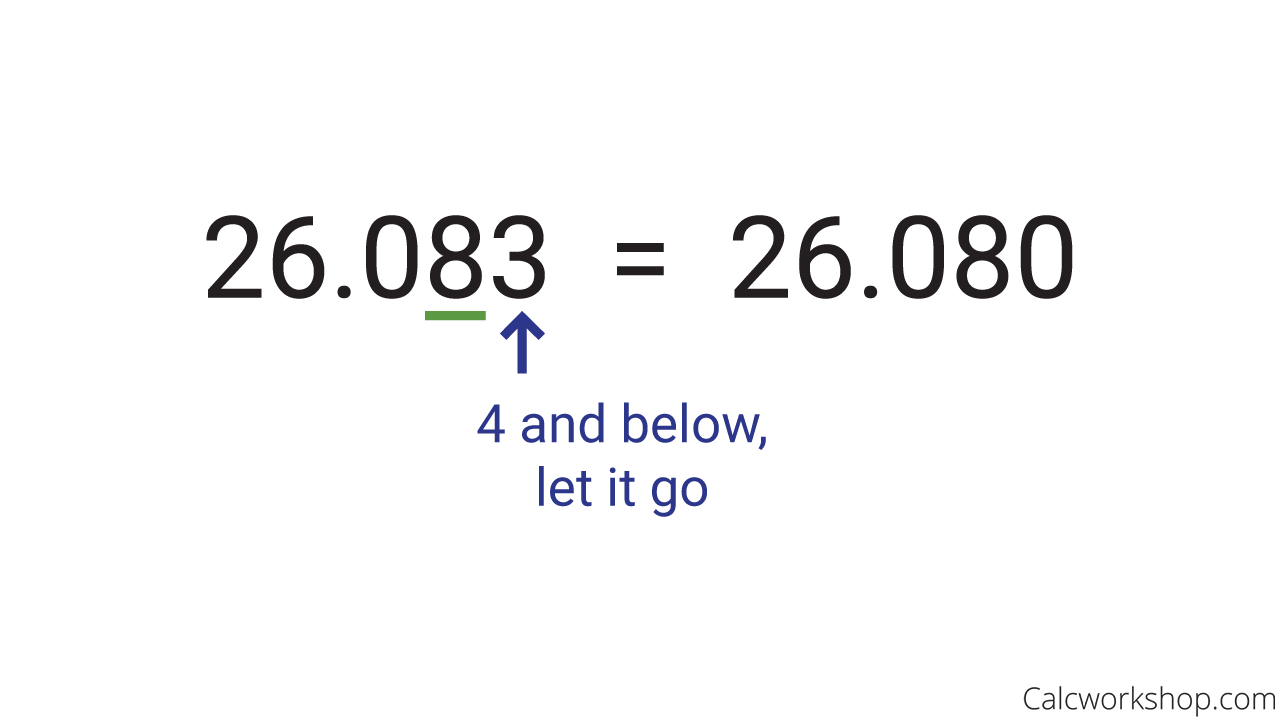
Rounding Down A Decimal

Next, let’s investigate rounding decimals to the indicated place value. Such as, round to the nearest tenth, nearest hundredth.

Rounding To The Hundredths Place

Another important rounding skill is knowing how to round to the nearest whole number. All this means is that we want to round our number to the “ones” place or the digit in front of the decimal point as noted by SplashLearn.

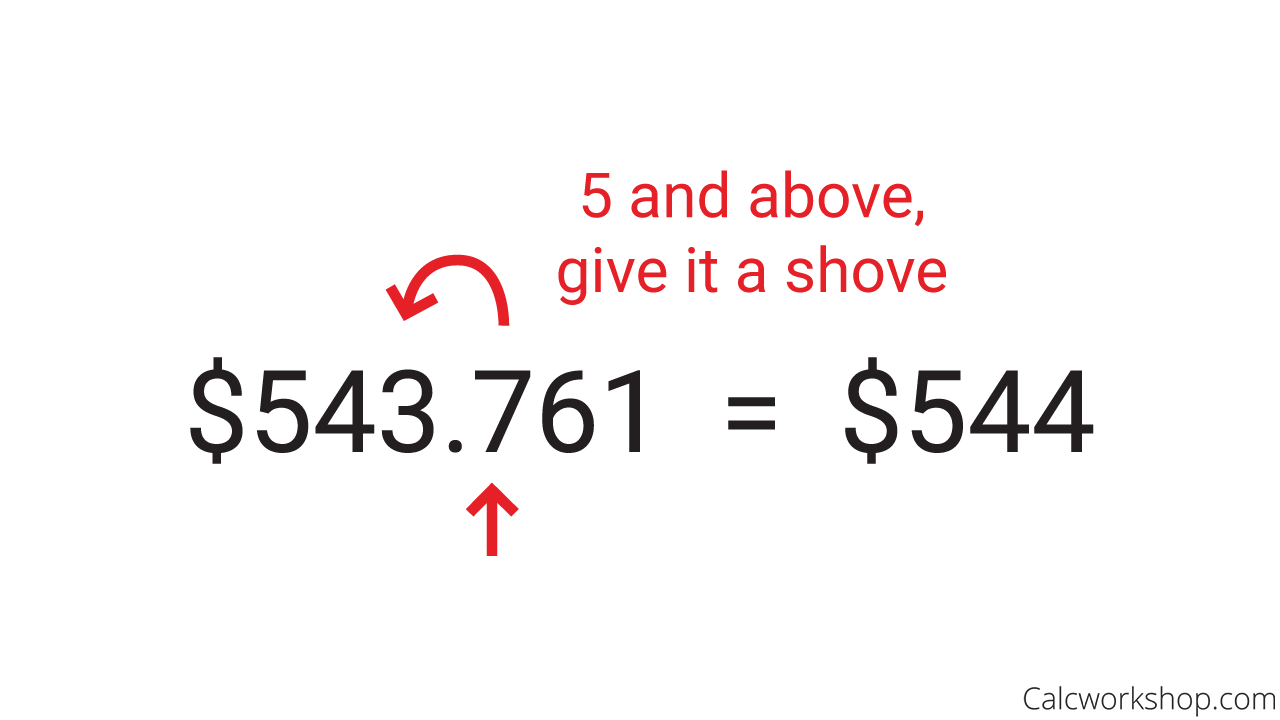
Round Up To The Nearest Whole Number

Why is this a necessary skill?

Because it allows us to communicate effectively and helps us to perform a simple mathematical operation in our head.

For example, adding 105.279 and 459.912 is rather tricky to do in your head, but if we round our numbers first, the calculation becomes a lot easier 105 + 460.

Significant Figures

Next, let’s talk about significant figures.

Significant figures also called significant digits or sig figs for short, are a convenient way across the mathematics and science communities for indicating the digits of a number that are meaningful in terms of precision or accuracy.

You will need to know how to recognize the number of significant figures and how to round to the appropriate significant digit in many of your future math and science courses, so understanding and knowing the rules is essential.

So, let’s look at the rules for significant figures!

Rules

First, any non-zero numbers ARE significant.

• 123.456 has six significant digits
• 5.12 has three significant digits

Second, any zeros between two non-zero digits ARE significant.

• 3079 has four significant digits
• 82003 has five significant digits

Third, trailing zeros when there is a decimal point is significant.

• 22.0 has three significant digits
• 127.930 has six significant digits
• 90. has two significant digits

Fourth, leading zeros are NOT significant.

• 0.01328 has four significant digits
• 0.0002 has one significant digit

Lastly, trailing zeros in a whole number is NOT significant.

• 7890 has three significant digits
• 90 has one significant digits

Even with the steps and examples above, determining the number of significant figures can be tricky. Thankfully we will walk through numerous examples and look at how to round a number to the desired number of significant figures.

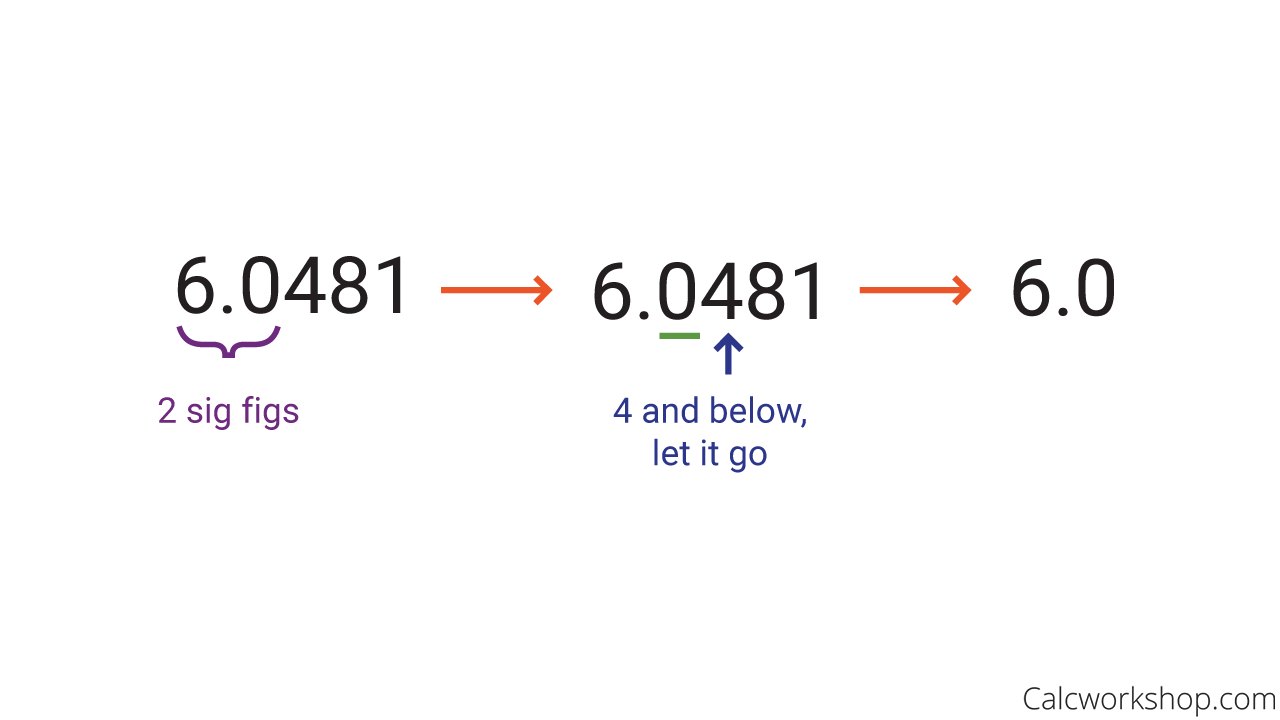
Rounding To Two Significant Figures

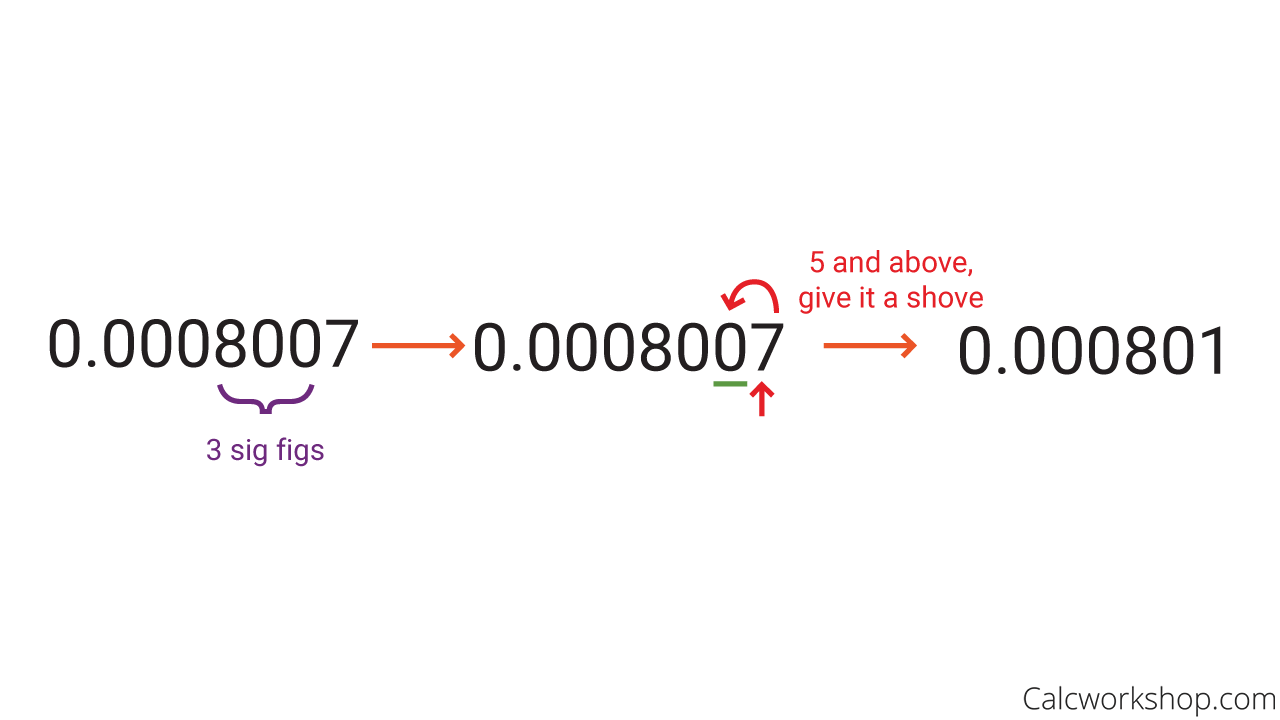
Rounding To Three Significant Figures

Worksheet (PDF) — Hands on Practice

It’s all fun and games until you try it on your own. So give these worksheets a go — and improve your knowledge!

Practice Problems
Step-by-Step Solutions

Don’t worry. It will all make sense once you see it in action.

Throughout the video, we will apply our rounding rules for decimals and significant figures, and see how easy and useful rounding can be.

Let’s get to it!

Rounding Decimals – Lesson & Examples (Video)

42 min

• Introduction to Video: Rounding Decimals and Significant Figures
• 00:00:31 – What are the rules for rounding decimals? with (Examples #1-2)

• 00:09:38 – Round each decimal to the indicated place (Examples #3-6)
• 00:17:48 – Round to the nearest whole number or unit of measure (Examples #7-13)
• 00:23:42 – What are significant digits? What are the rules of significant figures?
• 00:32:00 – Determine the number of significant figures (Examples #14-20)
• 00:35:54 – Round to the desired number of significant digits (Examples #21-27)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions