Why do we need the Exponential distribution or the Gamma distribution?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
To predict the wait time until future events occur!
For example:
- The time between arrivals at an airport or train station.
- Or the amount of time until an equipment failure.
- Or even the amount of time until the next earthquake.
Exponential Vs Gamma Distribution
The difference between the gamma distribution and exponential distribution is that the exponential distribution predicts the wait time until the first event. In contrast, the gamma distribution indicates the wait time until the kth event.
But before we can look at these two distributions, we have to know where they come from. The Exponential random variable comes from the Gamma random variable, and the Gamma distribution comes from the Gamma function.
While the scope of the gamma function is explored in such classes as complex analysis, it is used in statistics, probability, and combinatorics, and it helps us generalize factorials.
Here are some critical Gamma Function properties that we will be using in our analysis of the gamma distribution:
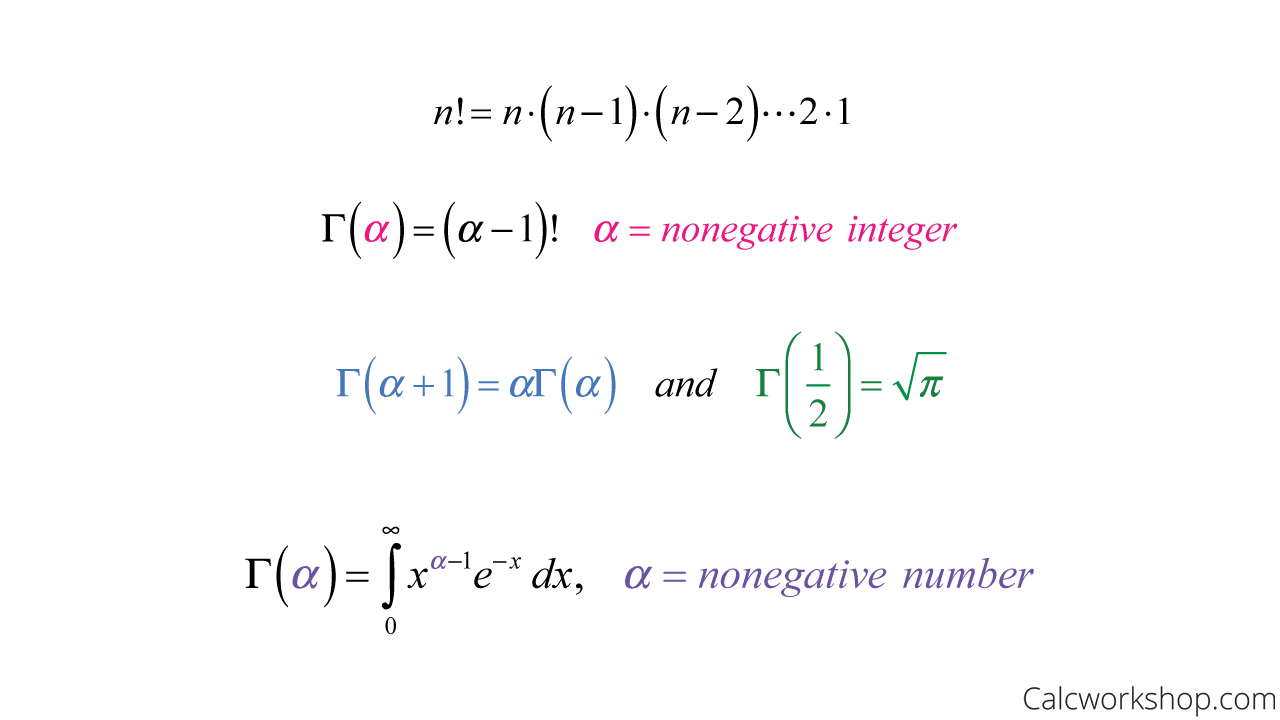
Gamma Function Properties
To really see the importance of these properties, let’s see them in action.
Gamma Distribution
Let’s use the properties of the gamma function to evaluate the following values:
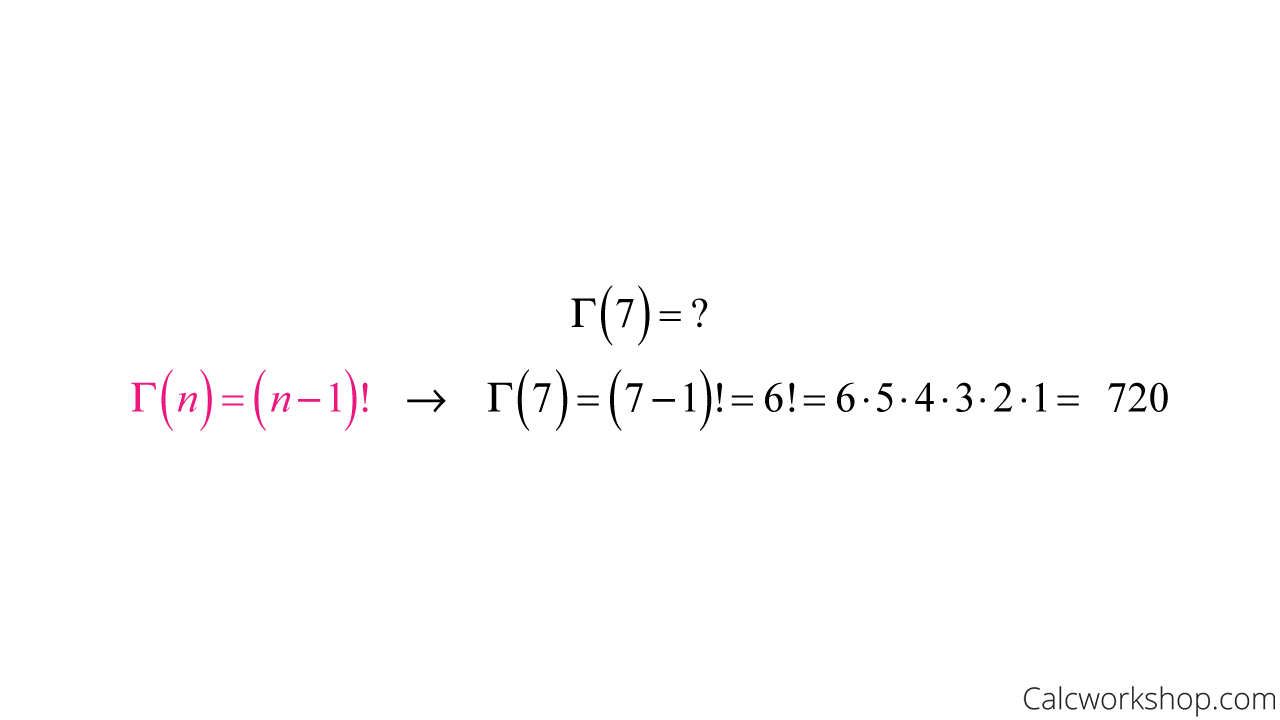
Gamma Function (Positive Integer)
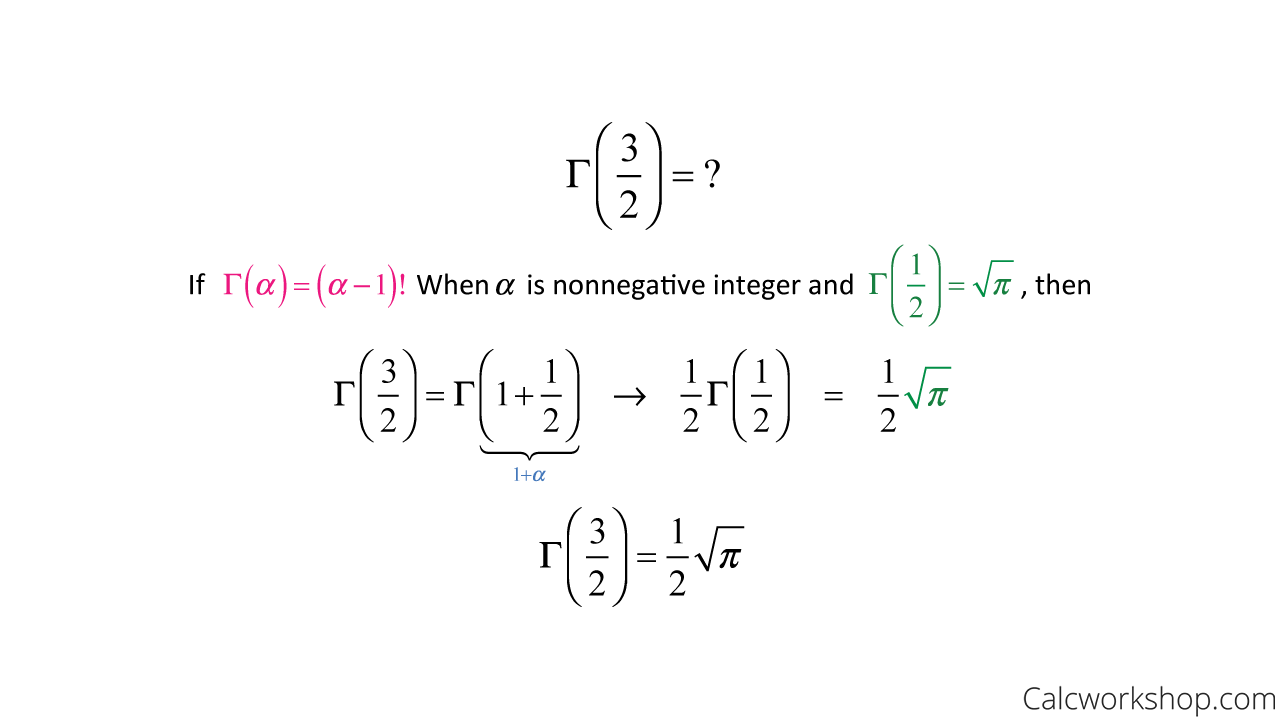
Gamma Function (Square Root of Pi)
Now that we’ve gotten a taste of the gamma function let’s explore the Gamma Distribution.
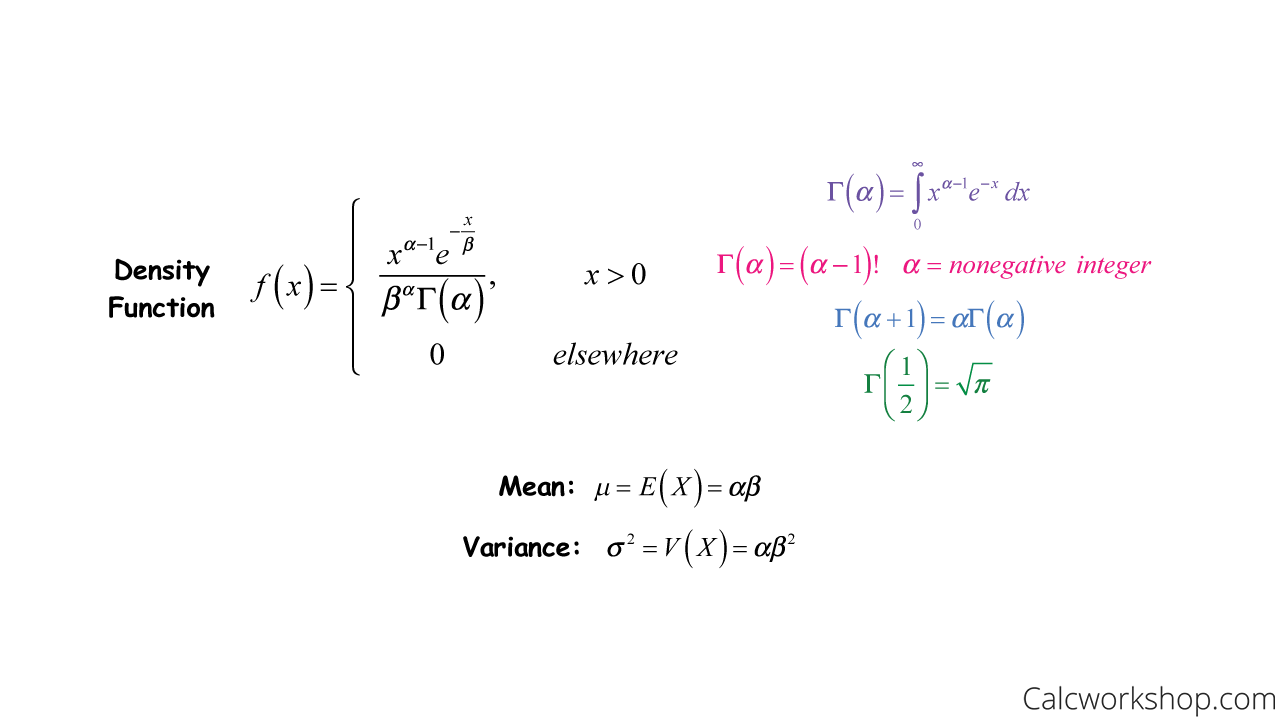
Gamma Distribution Formulas
Additionally, there are two exceptional cases of the Gamma Distribution: Erlang and Exponential.
What this means is that the Gamma distribution is used when alpha is any positive real number, the Erlang distribution is a particular case of the gamma distribution where alpha is a positive integer only, and the Exponential distribution is a gamma distribution where alpha is equal to one.

Gamma — Erlang — Exponential Differences
This shows that the Gamma distribution predicts the wait time until the alpha event occurs, the Poisson distribution predicts the number of events in an interval, and the Exponential distribution predicts the wait time until the first event occurs.
Exponential Distribution
Okay, so now let’s explore the Exponential Distribution more closely.
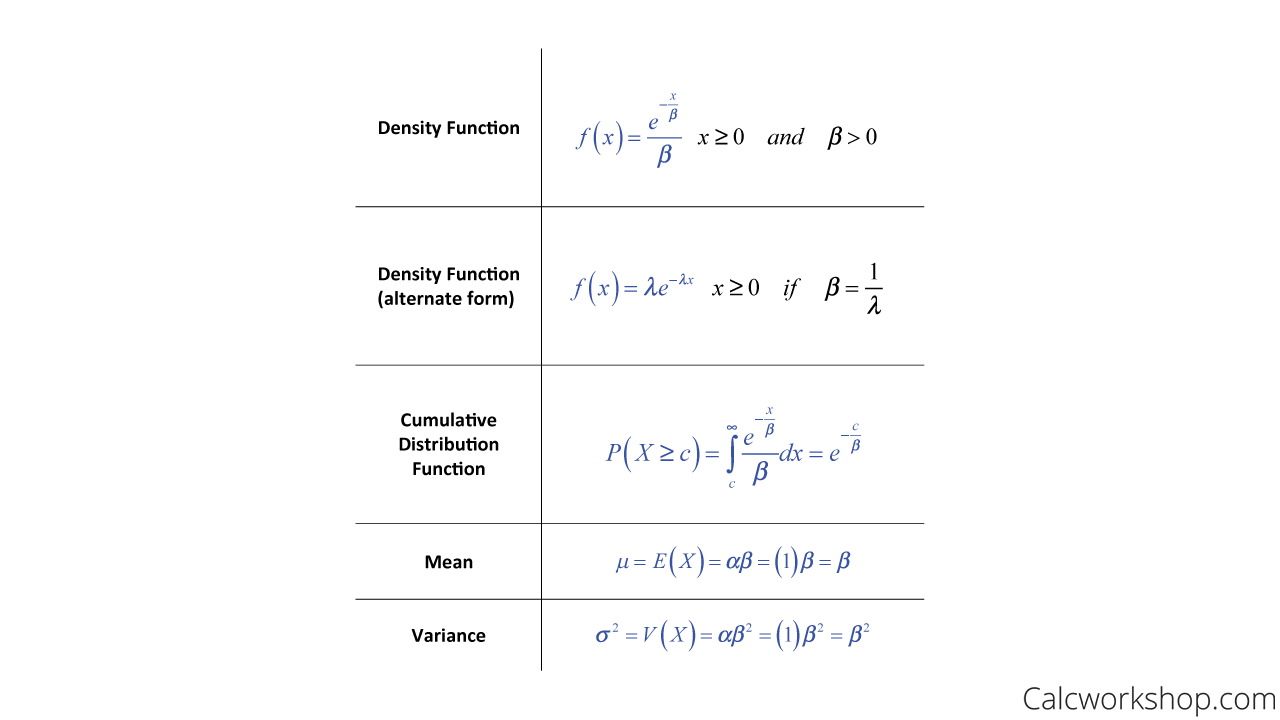
Exponential Distribution Formulas
Please note that some textbooks will use different variables like m or k or even lambda in place of alpha. So, if you see these other variables in your studies, don’t worry as they all mean the same thing.
Additionally, it is important to point out that beta (lambda) is also referred to as the rate parameter, as it is used to model failure rate.
Example
Alright, so let’s look at an example.
Suppose the time between calls to a handyman business is exponentially distributed with a mean time between calls of 15 minutes. What is the probability that the first call arrives within 5 and 8 minutes of opening?
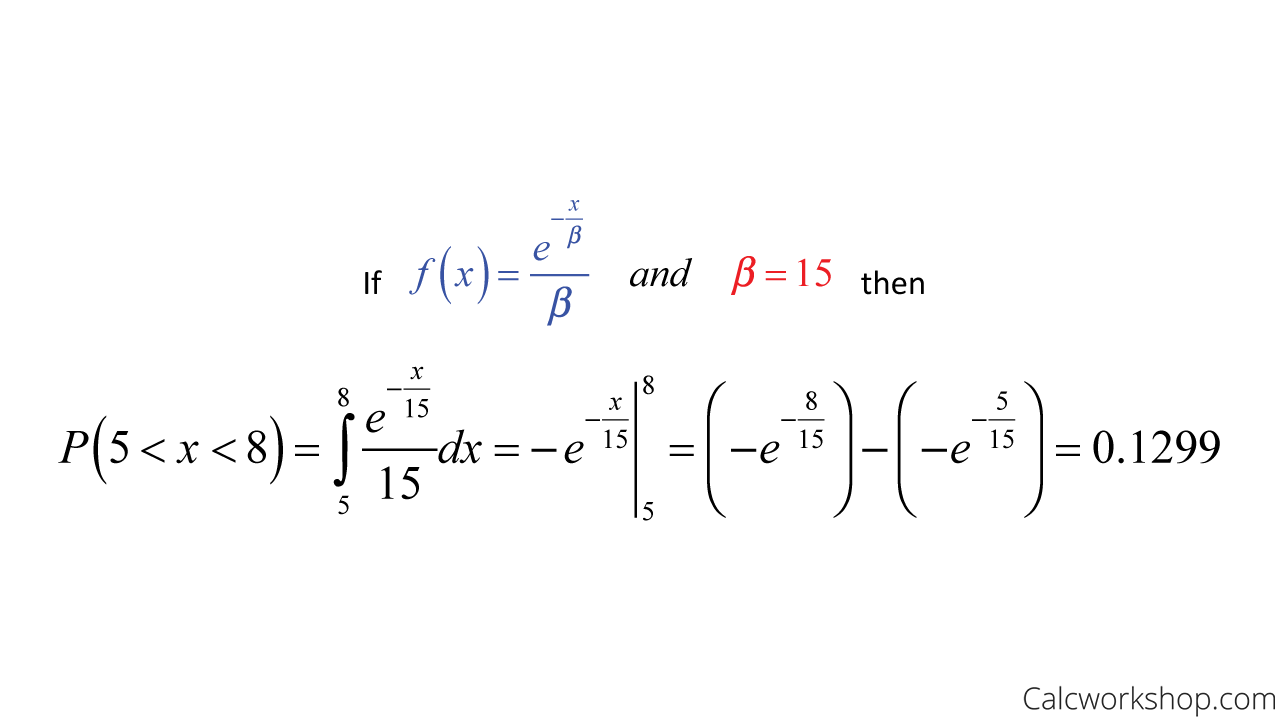
Exponential Distribution — Example
So this means that we are able to determine that the probability of the first call arrives within 5 and 8 minutes of opening is 0.1299.
And did you know that the exponential distribution is memoryless?
Memoryless Property
The Exponential Distribution has what is sometimes called the forgetfulness property.
This means that if a component “makes it” to t hours, the likelihood that the component will last additional r hours is the same as the probability of lasting t hours. In other words, the past wait time has no bearing on the future wait time as noted by Towards Data Science. Every instant is like the beginning of a new time interval, so we have the same distribution regardless of how much wait time has already passed.
Cool!
This video will look at the memoryless property, the gamma function, gamma distribution, and the exponential distribution along with their formulas and properties as we determine the probability, expectancy, and variance.
Exponential Distribution – Lesson & Examples (Video)
1 hr 30 min
- Introduction to Video: Gamma and Exponential Distributions
- 00:00:41 – Overview of the Gamma Function and Gamma Distribution
- Exclusive Content for Members Only
- 00:15:15 – How to use the Gamma distribution properties and density function (Examples #1-2)
- 00:38:15 – Overview of the Erlang and Exponential Distribution and its properties
- 00:45:53 – Use integration of the exponential distribution density function to find probability (Example #3)
- 00:49:20 – Generate the exponential cumulative distribution function formulas
- 00:39:39 – Find the probabilities for the exponential distribution (Examples #4-5)
- 01:04:26 – Determine the probabilities for the exponential distribution (Example #6-7)
- 01:17:13 – Lack of Memory Principle for the Exponential Distribution with (Examples #8-9)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.