Did you know that finding the probability of a continuous random variable is nothing more than using integration?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true.
Let’s jump in to see how this really works!
Discrete Vs Continuous
What’s the difference between a discrete random variable and a continuous random variable?
A discrete random variable is a one that can take on a finite or countable infinite sequence of elements as noted by the University of Florida. In contrast, a continuous random variable is a one that can take on any value of a specified domain (i.e., any value in an interval).
For example, the height of students in a class, the amount of ice tea in a glass, the change in temperature throughout a day, and the number of hours a person works in a week all contain a range of values in an interval, thus continuous random variables.
What is important to note is that discrete random variables use a probability mass function (PMF) but for continuous random variables, we say it is a probability density function (PDF), or just density function.
Formulas
The properties of a continuous probability density function are as follows.
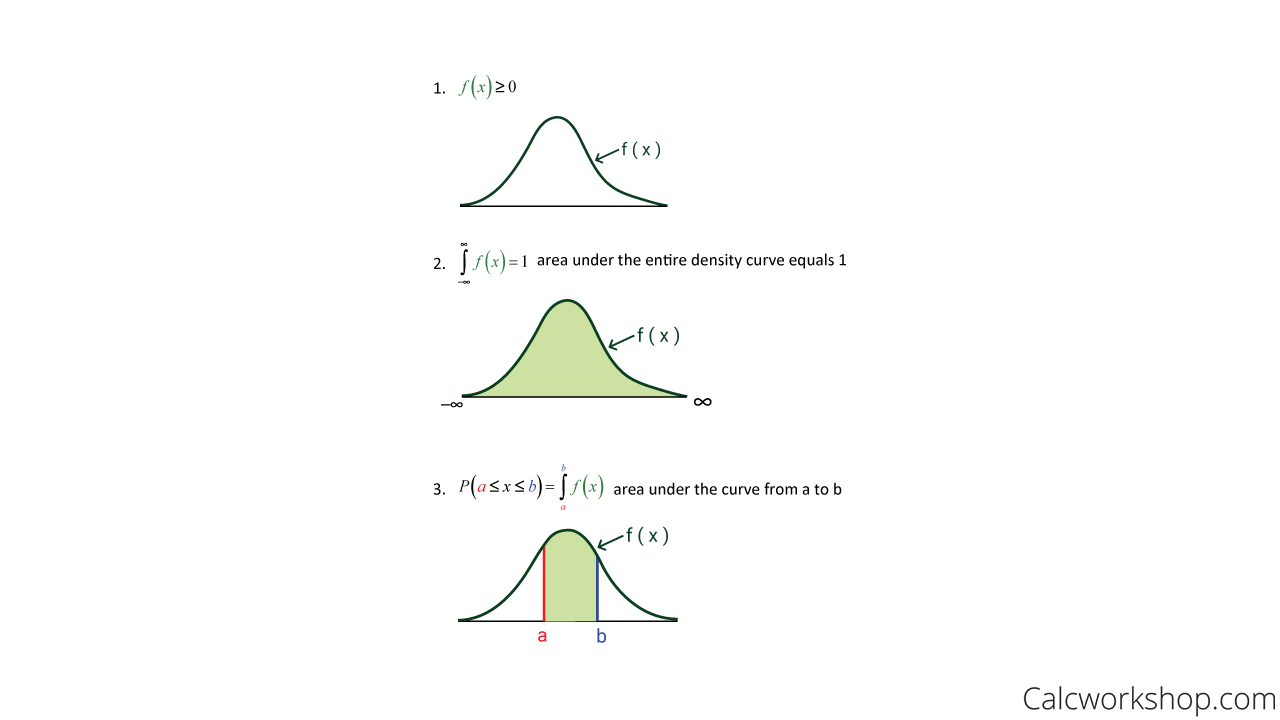
Probability Density Function
So, to find the probability, we just need to integrate over the region using our knowledge of the Fundamental Theorem of Calculus!
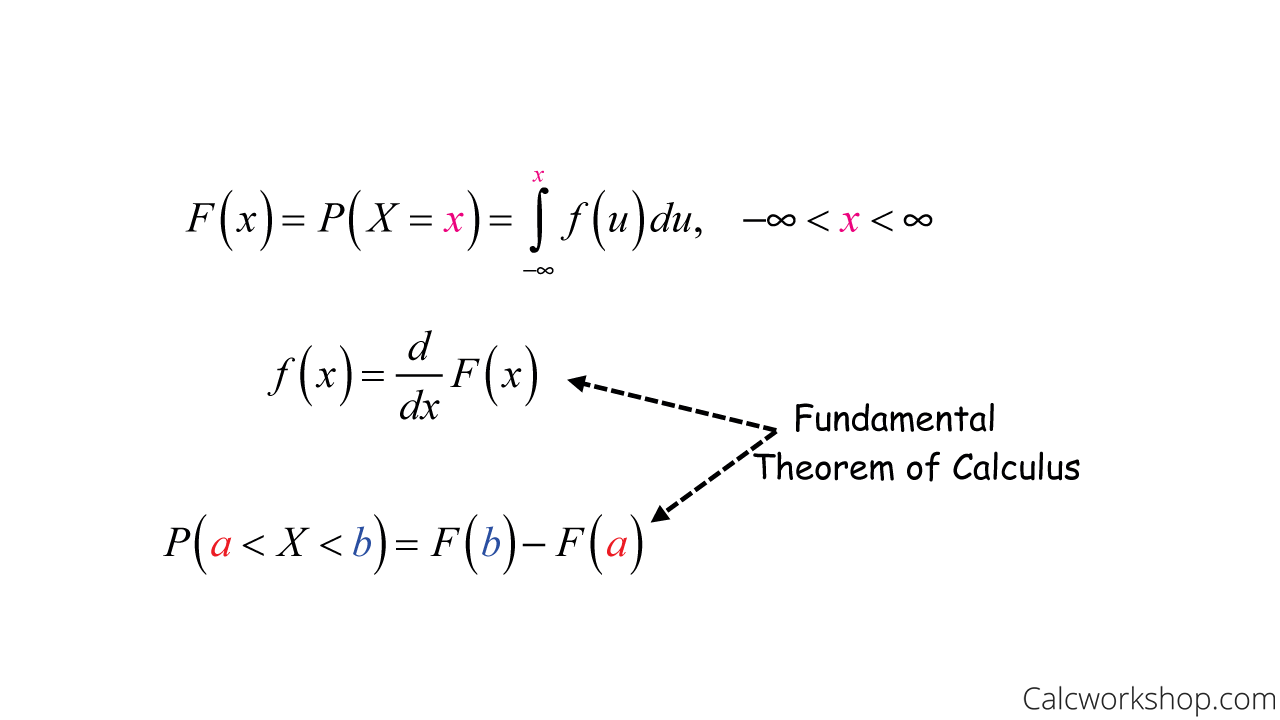
CDF Formula
Worked Example – CDF
Let’s look at an example.
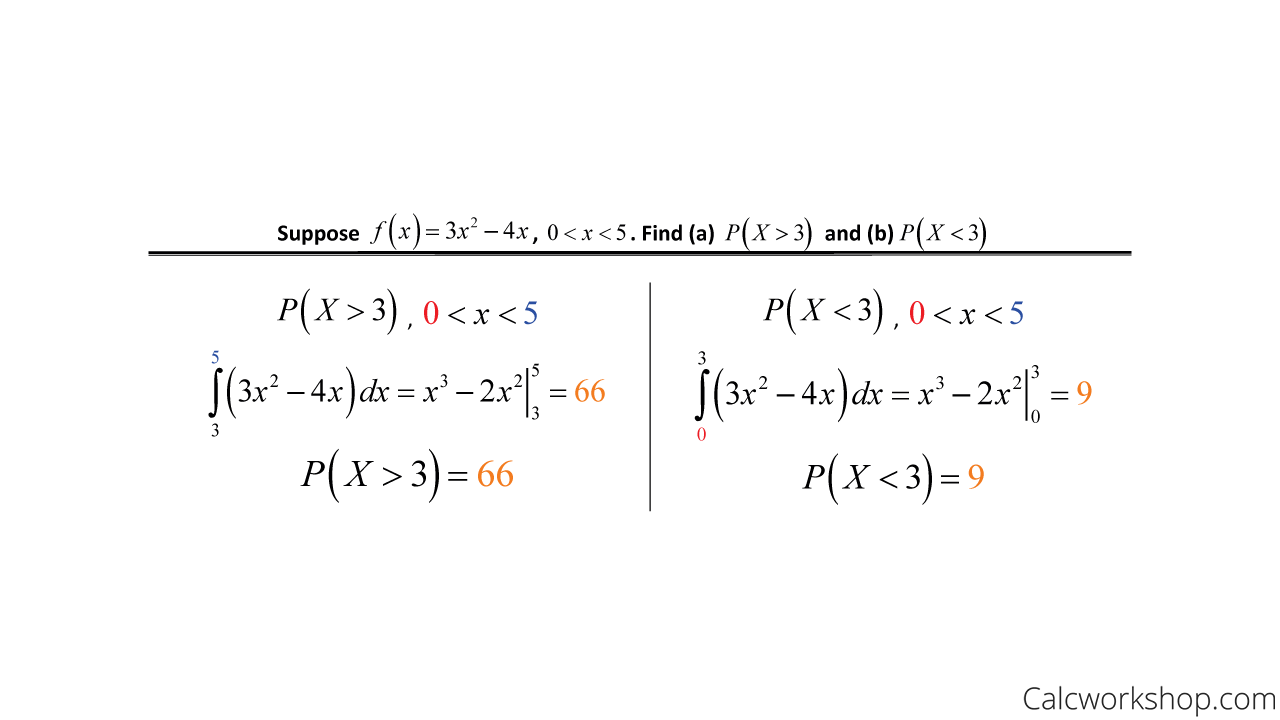
Continuous CDF Probability Example
Now here is what’s really cool…
…all PDF curves equal the probability of the corresponding range of outcomes from the sample space.
We define a cumulative density function (CDF) to calculate the area under the curve in these instances. This means that the cumulative density equals the probability that the random variable is less than or equal to a number x.
Here’s an example of how we determine the cumulative distribution function for the continuous random variable over a specified range.
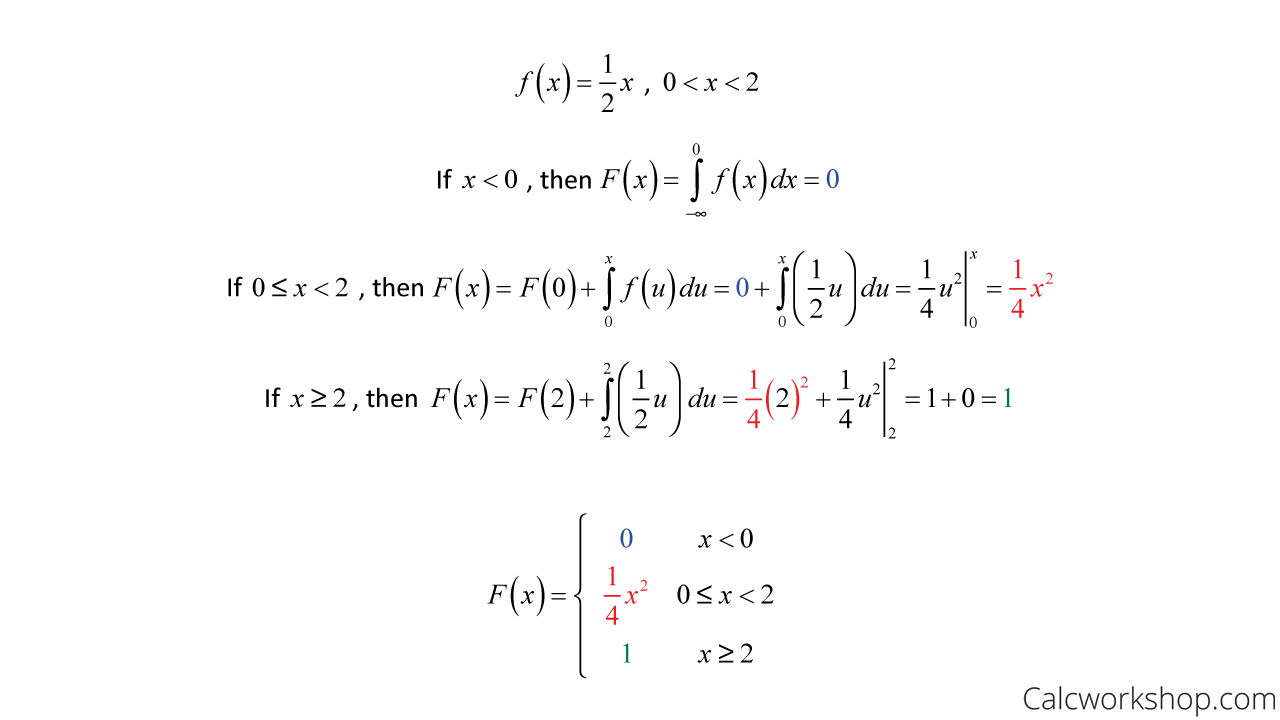
Continuous Random Variable Example
This video will walk through numerous examples of how to find probability using the probability density function and how to create the cumulative distribution function over a sample space.
Continuous Random Variable – Lesson & Examples (Video)
1 hr 21 min
- Introduction to Video: Continuous Random Variables
- 00:00:33 – Overview and Properties of Continuous Probability Distributions
- Exclusive Content for Members Only
- 00:09:09 – Given the density function for a continuous random variable find the probability
- 00:18:21 – Determine x for the given probability (Example #2)
- 00:29:32 – Discover the constant c for the continuous random variable (Example #3)
- 00:34:20 – Construct the cumulative distribution function and use the cdf to find probability (Examples#4-5)
- 00:45:23 – For a continuous random variable find the probability and cumulative distribution (Example #6)
- 00:54:11 – Given the cumulative distribution function find the probability density function (Example #7)
- 00:57:56 – Graph the probability density function and verify f(x) is a pdf (Example #8a-b)
- 01:06:58 – Find the cumulative distribution function (Example #8c)
- 01:17:39 – Use the cumulative distribution function to find the probability (Example #8d)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.