As we have already seen, there are some pretty cool properties when it comes triangles, and the Midsegment Theorem is one of them.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
The Midsegment Theorem states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half as long. And seeing as there are three sides to a triangle, that means there are three midsegments of a triangle as well.
But the amazingness does stop there!
Because the midsegments are parallel to the third side we are able to use angle pair relationships such as corresponding, alternate interior, and same-side interior, to find the measure of interior angles.
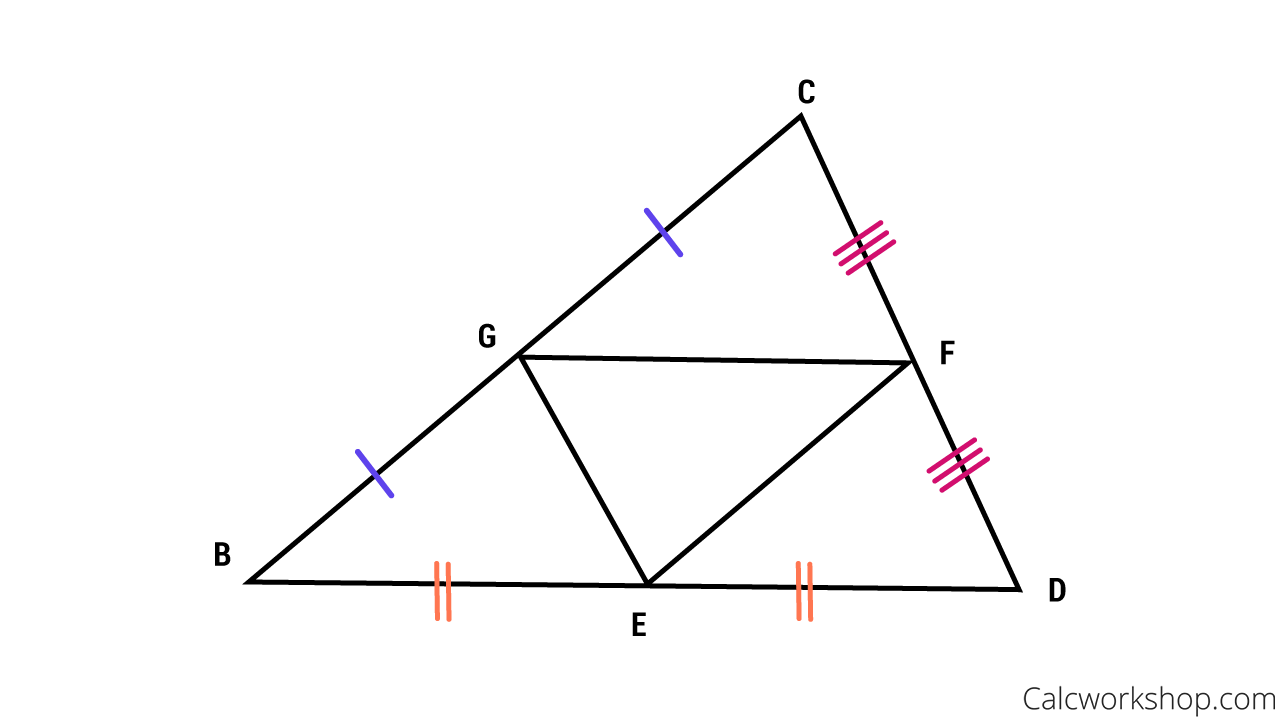
Triangle Midsegment Theorem Example
Additionally, did you know that the positions of the longest and shortest sides of a triangle correspond to the positions of its opposite angles?
This means that the largest angle is always opposite the longest side, and the smallest angle is opposite the shortest side.
Empowered with the ability to create triangle inequalities, we are then able to show that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side. This is called the Triangle Inequality Theorem, as Math Warehouse accurately states.
What this means is that we are able to determine if a triangle exists just by looking at the three sides of a triangle!
Cool!
Lastly, the Hinge Theorem enables us to compare one triangle with another by comparing angle or side lengths.
Suppose you are in a house with lots of different rooms. You open one door just large enough to fit through, but when you open a second door you open the door all the way before entering.
What you will notice is that the opening length of the first door is shorter because the angle created from the hinge on the door is smaller. Whereas the opening length of the second door is larger because the angle created by the hinge is larger.
And just like the hinge on a door, the larger the angle we create the greater the opening to walk through, the Hinge Theorem allows us to represent angles and side lengths between two triangles!
The Hinge Theorem states that if two sides of one triangle are congruent to two sides of another triangle, and the included angle of the first is larger than the included angle of the second, then the third side of the first triangle is longer than the third side of the second triangle. The converse is also true.
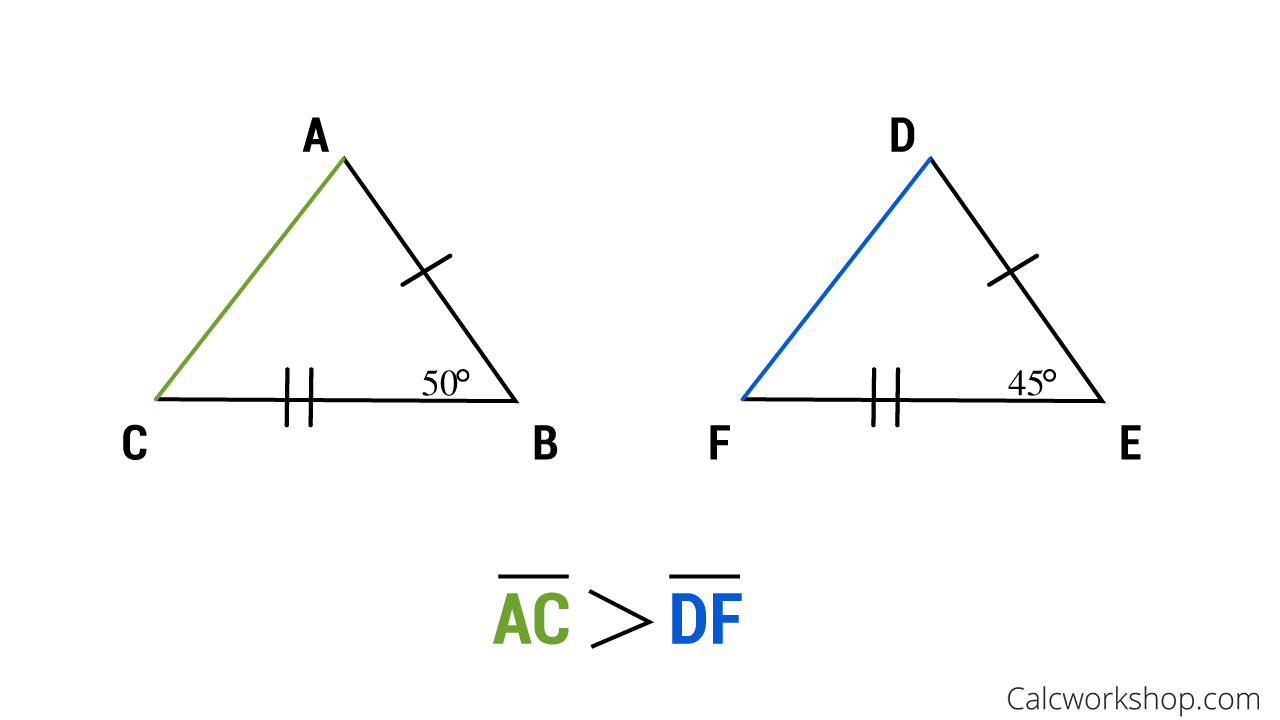
Hinge Theorem Comparing Side
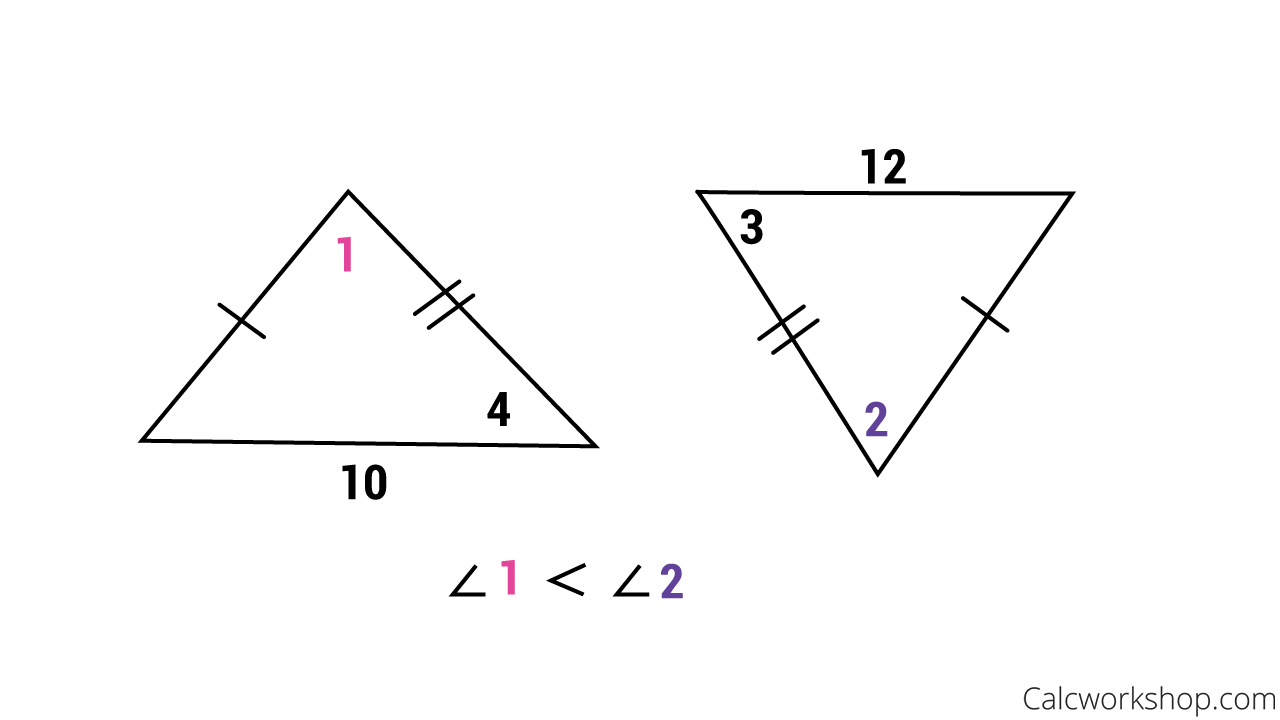
Hinge Theorem Comparing Angles
Together we are going to look at countless examples of how to accurately apply the Midsegment Theorem to find angle measure and side lengths as well as the perimeter. We will then create triangle inequalities, determine if a triangle exists given three sides of a triangle, and use the Hinge Theorem to compare two triangles and find indicated measures.
Triangle Midsegment Theorem – Lesson & Examples (Video)
1 hr 4 min
- Midsegment & hinge theorem introductions
- 00:00:43 – Overview of the midsegment theorem (Examples #1-8)
- Exclusive Content for Member’s Only
- 00:18:36 – Use the midsegment theorem to find the indicated measure (Example #9)
- 00:24:17 – Complete the two-column proof given midsegments of a triangle (Example #10)
- 00:30:36 – Overview of the triangle inequality theorem, exterior angle inequality, and the hinge theorem
- 00:39:14 – List the sides and angles in order from least to greatest and determine if the triangle exists (Examples #11-18)
- 00:47:39 – Given the triangle, create an inequality and solve for x (Examples #19-20)
- 00:52:58 – Complete each statement with less than, greater than, or equal to (Examples #21-24)
- 00:57:53 – Use the hinge theorem to solve for x (Examples #25-27)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.