Did you know that the three medians of a triangle intersect to form the centroid of the triangle? And that the centroid is the balancing point or the triangle’s center of mass!

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Exciting!
In today’s geometry lesson, we’re going to use these new properties to find missing side lengths and angles.
Explore what altitudes of triangles are and how they compare and contrast with medians.
Let’s go!
What is the Median of a Triangle?
A median is a segment from a vertex of the triangle to the midpoint of the opposite side. And each triangle has three medians.
Centroid
Furthermore, the concurrent point, or centroid, of all three medians is located two-thirds of the distance from each vertex to the midpoint of the opposite side. This is called the Centroid Theorem, or the Concurrency of Medians Theorem as ck-12 accurately states.
So by understanding medians of a triangle and applying the centroid theorem, we can find missing side lengths of triangles.
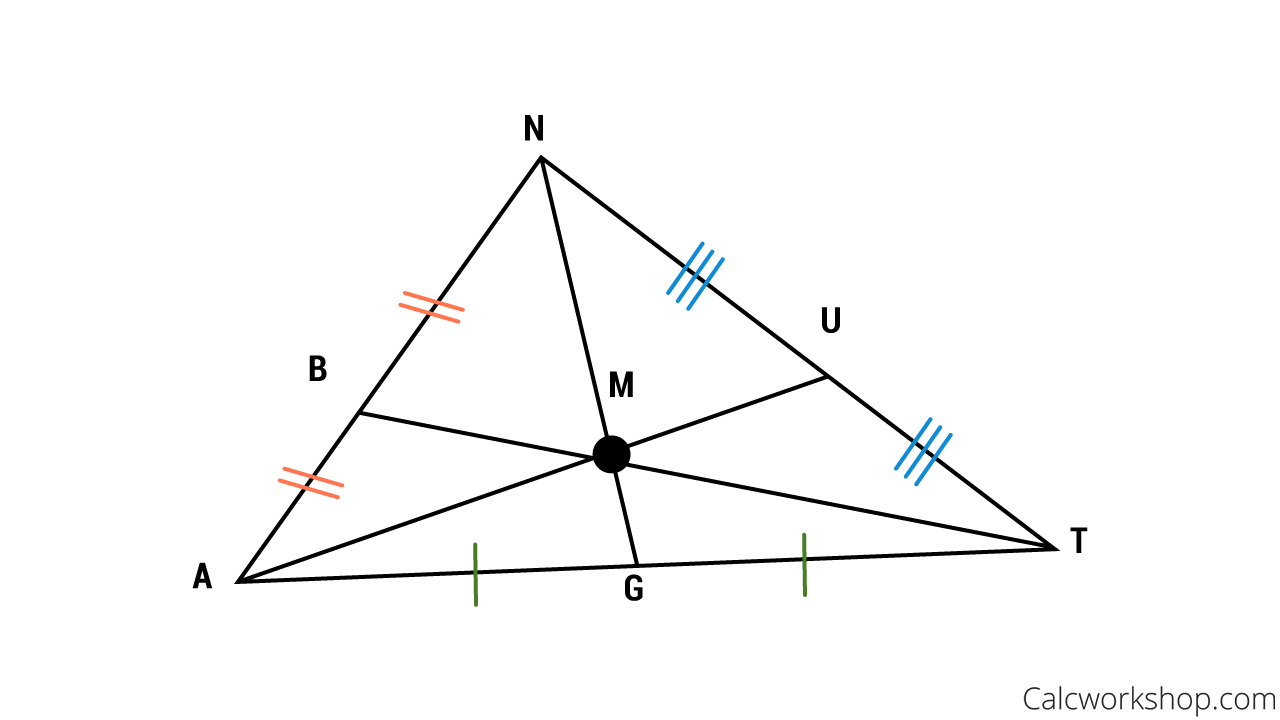
Centroid of a Triangle
Using the image above, the medians of triangle ANT are AU, NG, and TB. The three medians intersect, or are concurrent, at point M. Point M is the centroid of triangle ANT.
What is the Altitude of a Triangle?
Now the altitude of a triangle is a segment that is also drawn from the vertex of a triangle. But this segment is perpendicular to the opposite side. Additionally, every triangle also has three altitudes, and their point of concurrency is called the orthocenter of the triangle.
Orthocenter
What’s so important about altitudes and the orthocenter? They enable us to find the values of angles inside a triangle quickly.
Moreover, there are some really interesting facts regarding the centroid and orthocenter of triangles, as they relate to the circumcenter and incenter of triangles!
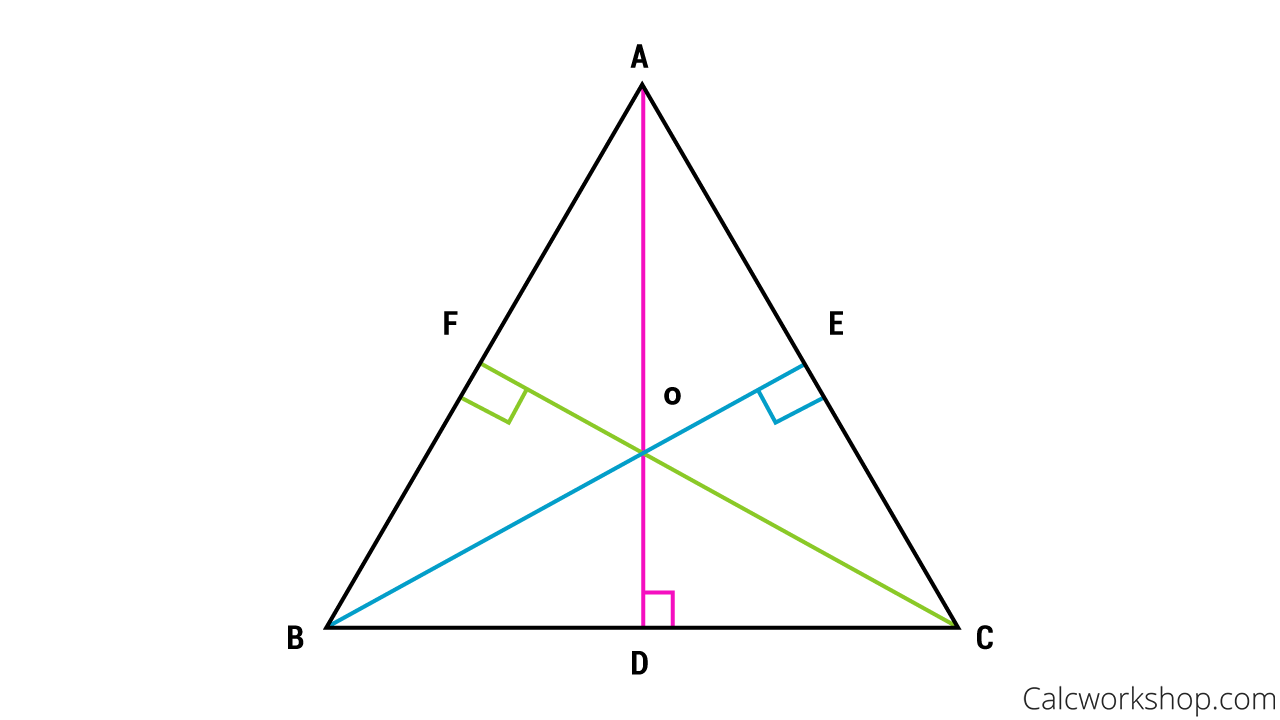
Orthocenter of a Triangle
Looking at the figure above, the altitudes AD, BE, and CF intersect, or are concurrent, at point O. Point O is the orthocenter of triangle ABC.
In the video below, we will explore various problems for finding missing side lengths and angles given medians and altitudes.
Also, will determine the coordinate of the centroid given three vertices, and learn the distinguishing characteristics between perpendicular bisectors (circumcenter), angle bisectors (incenter), medians (centroids), and altitudes (orthocenter).
Medians and Altitudes – Lesson & Examples (Video)
37 min
- Medians and altitudes introduction
- 00:00:35 – Medians of triangles and the centroid theorem
- 00:06:40 – Find the indicated measures given the median of a triangle (Examples #1-2)
- Exclusive Content for Member’s Only
- 00:15:50 – Find the indicated measures given one or more medians (Examples #3-4)
- 00:20:30 – Find the indicates measures given two medians of the triangle (Examples #5-6)
- 00:46:31 – How to find the coordinate of the centroid given vertices (Examples #7-8)
- 00:53:01 – Altitudes of triangles and the orthocenter (Example #9)
- 01:01:12 – Find the indicated measure given the altitude of the triangle (Examples #10-12)
- 01:14:30 – Determine if the segment is a median, an altitude, the perpendicular bisector, or an angle bisector (Example #13)
- 01:18:40 – Key facts about the circumcenter, incenter, centroid, and the orthocenter of triangles
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.