In today’s geometry lesson, you’re going to learn how to use the Hypotenuse Leg Theorem.
Up until now, we’ve have learned four out of five congruency postulates for triangles:

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
- Side-Angle-Side (SAS)
- Side-Side-Side (SSS)
- Angle-Side-Angle (ASA)
- Angle-Angle-Side (AAS)
Now it’s time to look at the final postulate for congruent triangles: Hypotenuse-Leg (HL).
What is the HL Postulate?
The HL Postulate states that if the hypotenuse and leg of one right triangle are congruent to the hypotenuse and leg of another right triangle, then the two triangles are congruent.
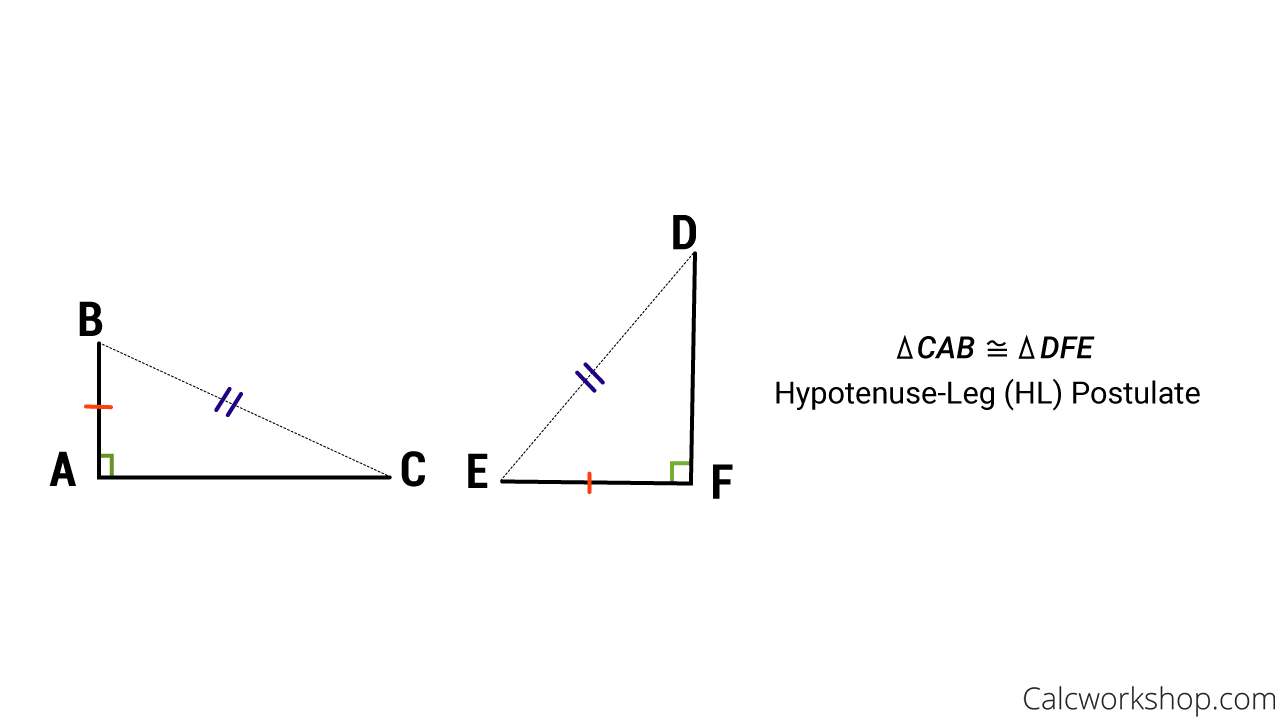
Hypotenuse Theorem Example
Using the image above, if segment AB is congruent to segment FE and segment BC is congruent to segment ED, then triangle CAB is congruent to triangle DFE.
Now, at first glance, it looks like we are going against our cardinal rule of not allowing side-side-angle…which spells the “bad word” (i.e., the reverse of SSA).
But thanks to the Pythagorean Theorem, and our ability to find the measure of the third angle, we can conclude that for right triangles only, this type of congruence is acceptable. In other words, with right triangles we change our congruency statement to reflect that one of our congruent sides is indeed the hypotenuse of the triangle.
Phew! No bad words here!
And with the last piece of the congruency puzzle finally unearthed we are going to combine our knowledge of triangle congruence with our understanding of both Isosceles Triangles and Equilateral Triangles.
Why?
Because right triangles are not the only types of triangles that have special properties – Isosceles and Equilateral Triangles are both pretty special. And right triangles, isosceles triangles, and equilateral triangles can work together to prove congruence and help us solve for missing sides and angles of triangles.
Now if we remember from when we learned to classify triangles, a triangle is isosceles if two sides of a triangle are congruent.
And just as we have two equal legs, an isosceles triangle has two equal legs (sides), as Math is Fun nicely points out. Well, if a triangle has exactly two congruent sides, then the base angles are congruent. The base angles are the two angles formed between the legs of the triangle and the non-congruent side. And more importantly, these base angles are congruent.
Isosceles Triangle Theorem
The Isosceles Triangle Theorem, sometimes called the Base Angle Theorem, states that if two sides of a triangle are congruent, then the angles opposite them are also congruent.
Equilateral Triangle Theorem
Moreover, the Equilateral Triangle Theorem states if a triangle is equilateral (i.e., all sides are equal) then it is also equiangular (i.e., all angles are equal). And if a triangle is equiangular, then it is also equilateral. Markedly, the measure of each angle in an equilateral triangle is 60 degrees.
Armed with our new information and knowledge, we are are going to:
- Learn how to solve for missing angle measures.
- Prove triangles are congruent using all five triangle congruency postulates.
- Continue to perfect our ability to write two-column proofs.
The HL Theorem – Lesson & Examples (Video)
37 min
- Introduction three triangle theorems
- 00:00:27 – Overview of the Hypotenuse-Leg Theorem, Isosceles Triangle Theorem, and the Equilateral Triangle Theorem
- Exclusive Content for Member’s Only
- 00:06:18 – In each figure, find the values of x and y using triangle properties (Examples #1-6)
- 00:20:28 – Given two parallel lines, find the value of each indicated angle (Example #7)
- 00:31:31 – If possible, prove the two triangles are congruent using SSS, SAS, ASA, AAS, or HL theorems (Examples #8-13)
- 00:41:30 – Complete the two-column proof (Examples #14-15)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.