What’s the difference between the Perpendicular Bisector Theorem and the Angle Bisector Theorem?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In today’s geometry lesson, that’s exactly what we’re going to find out!
You’ll learn the key differences between them and how to apply each method to multiple problems to find missing sides lengths and angles.
Here we go!
Perpendicular Bisector Theorem
So perpendicular bisector theorem states that if a point lies on the perpendicular bisector of a segment, then it is equidistant from the endpoints of that segment (i.e., equal length).
Which means, the perpendicular bisector theorem of a triangle tells us that if the sides of a triangle intersect at a point called the circumcenter, then the segments created from the vertices to the circumcenter of the triangle are equidistant (equal).
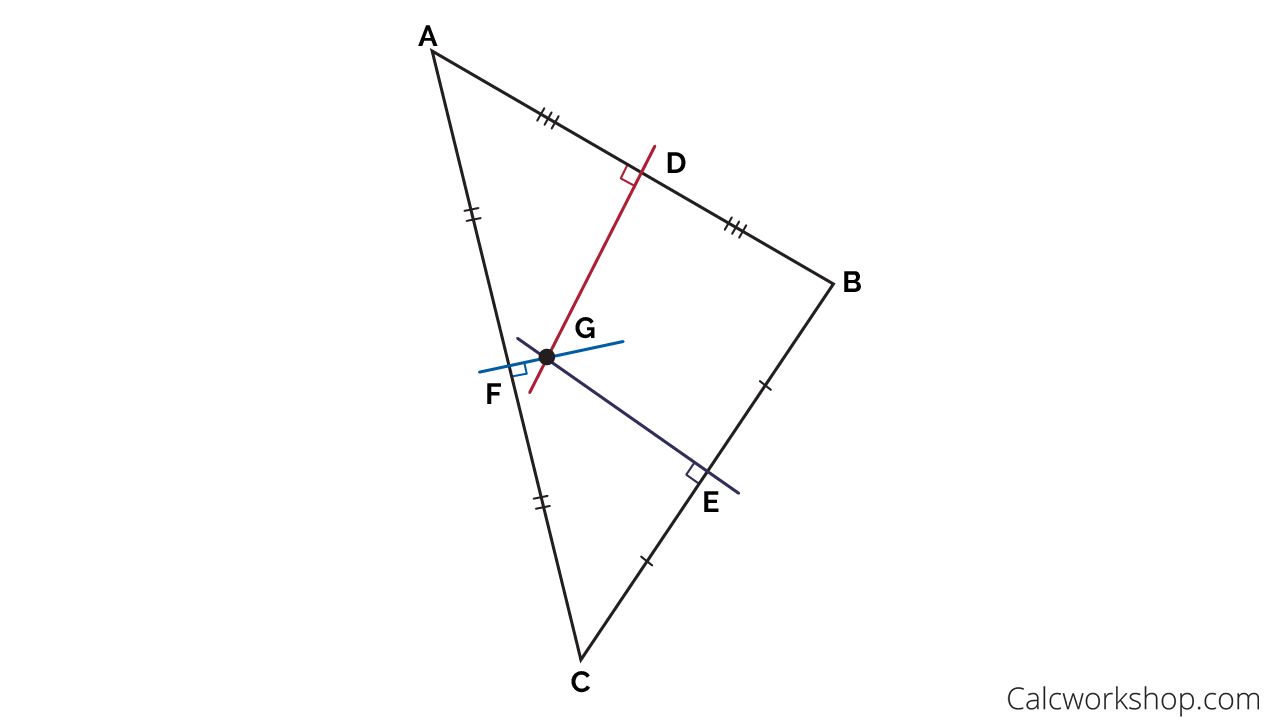
Perpendicular Bisector Theorem
As seen in the figure above, segment DG, segment EG, and segement FG are the three perpendicular bisectors of triangle ABC. Which means that point D is equidistant from points A and B, and point E is equidistant from points B and C, and point F is equidistant from points A and C. Point G is the circumcenter of triangle ABC.
An important note, the circumcenter is located in different places depending on which type of triangle you’re dealing with.
- Acute – Inside the triangle
- Right – On the triangle
- Obtuse – Outside the triangle
The video below goes into great detail on this topic.
Angle Bisector Theorem
Now the angle bisector theorem says that if a point is on the bisector of an angle, then it is equidistant from the two sides of the angle. In fact, the point where all the angle bisectors intersect is called the incenter of the triangle, and that is why the angle bisector theorem is sometimes called the incenter theorem.
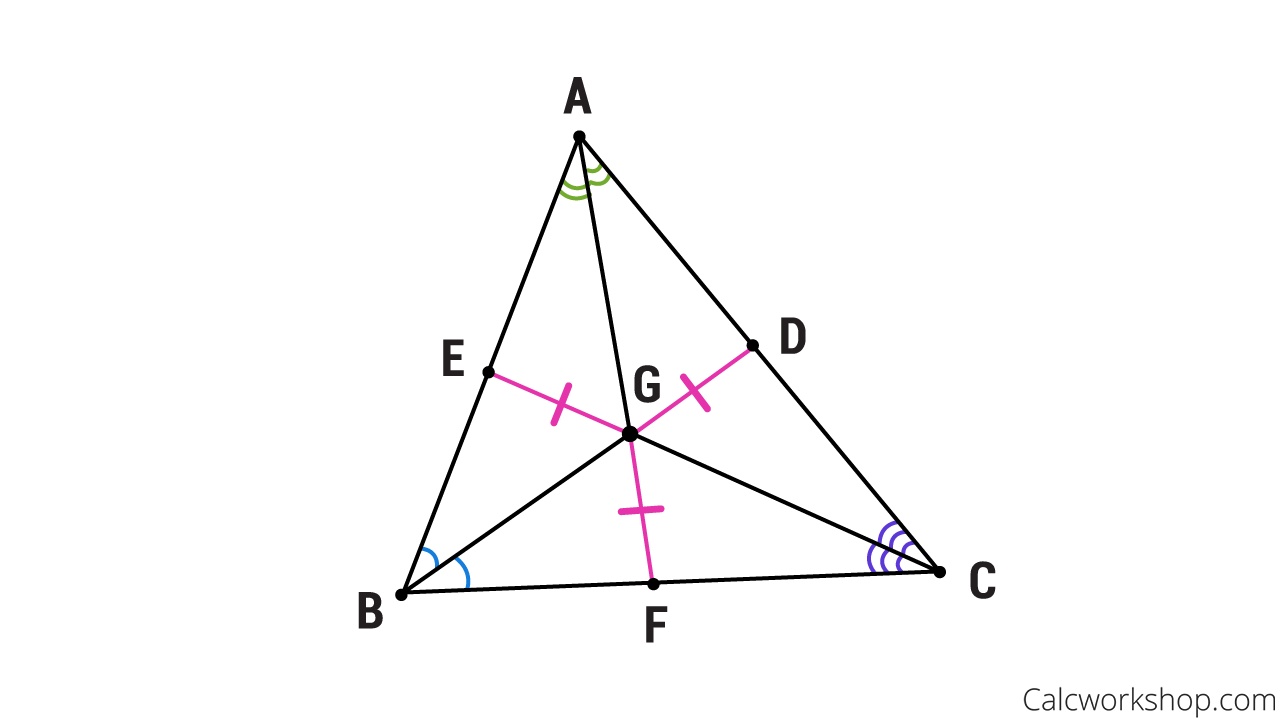
Angle Bisector Theorem Example
Using the triangle above, we can see that angle A is bisected by segment AF, angle B is bisected by segment BD, and angle C is bisected by segment CE, where segments AF, BD, and CE are called the angle bisectors of triangle ABC. Moreover, the three angle bisectors meet at point G, called the incenter.
What’s so confusing about these two theorems is that their drawings look almost identical, but their conclusions are different!
Perpendicular bisector theorem deals with congruent segments of a triangle, thus allowing for the diagonals from the vertices to the circumcenter to be congruent. Whereas the angle bisector theorem deals with congruent angles, hence creating equal distances from the incenter to the side of the triangle.
Yes, it’s confusing… but I’ve got tricks to help us figure this out!
But, why is this important?
Because by using our knowledge of midpoints, bisectors, pythagorean theorem, and our knowledge of congruent triangles we can find missing side lengths of a triangle if we are given the circumcenter or the incenter of a triangle (i.e., the point where all the perpendicular bisectors meet), as Varsity Tutors accurately states.
Together we will look at countless examples of perpendicular bisectors and angle bisectors to find the indicated measure, and never be confused again about the differences between the two!
Angle vs. Perpendicular Bisector Theorems – Lesson & Examples (Video)
37 min
- Introduction to angle and perpendicular bisector theorems
- 00:00:28 – Overview of the perpendicular bisector theorem and the circumcenter
- 00:14:15 – Overview of the angle bisector theorem and the incenter
- Exclusive Content for Member’s Only
- 00:24:52 – Use the perpendicular or angle bisector theorem to find the missing sides and angles (Examples #1-3)
- 00:41:07 – Find the indicated measure given the perpendicular bisector or angle bisector (Examples #4-6)
- 00:53:00 – Find the indicated measure given the angle bisector or perpendicular bisector (Examples #7-9)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.