Did you know that a sequence can be defined recursively and explicitly?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
What Is A Sequence
Formally, a sequence is an enumerated collection of objects, but informally, a sequence is a countable structure representing an ordered list of elements or numbers.

Definition Sequence
And we specify a sequence either recursively or explicitly.
Recursive Formula Definition
So, what is recursion?
A recursive definition, sometimes called an inductive definition, consists of two parts:
- Recurrence Relation
- Initial Condition
A recurrence relation is an equation that uses a rule to generate the next term in the sequence from the previous term or terms. In other words, a recurrence relation is an equation that is defined in terms of itself.
And all recurrence relations must come with an initial condition, which is a list of one or more terms of the sequence that precede the first term where the recurrence relation starts.
Example
For instance,
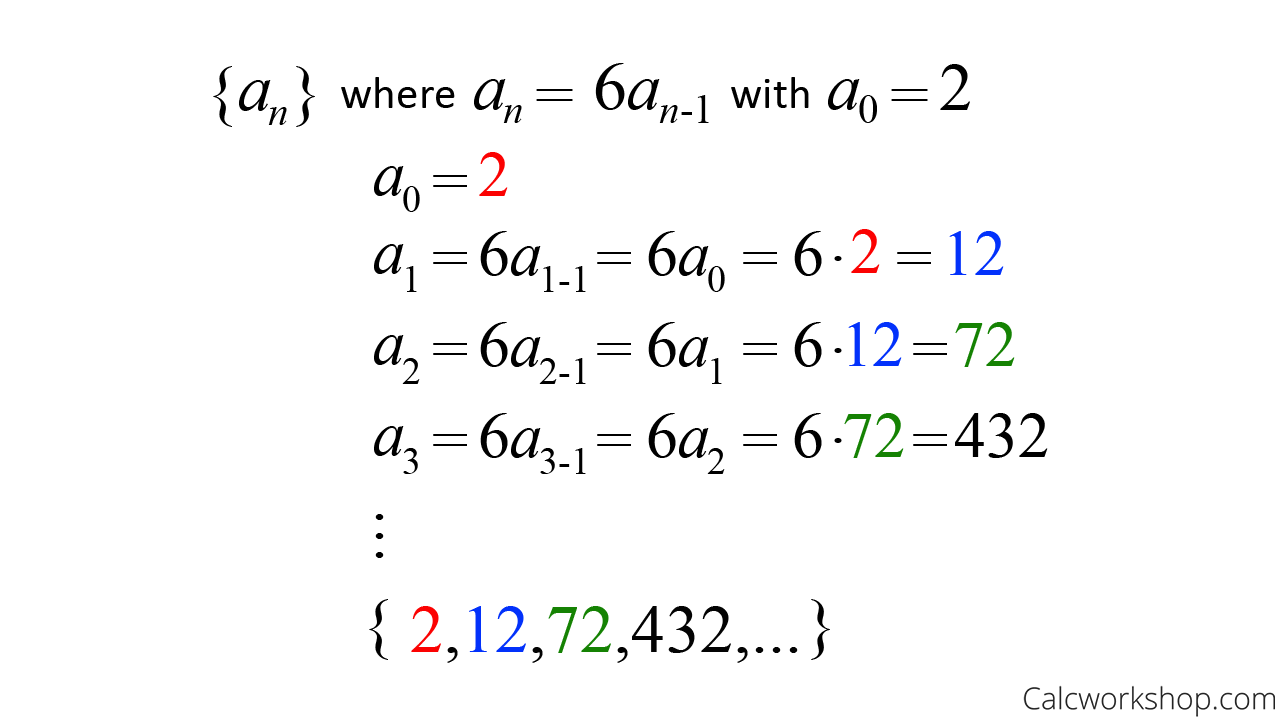
List Terms Recursive — Example
Notice that this looks just like the procedure we use for mathematical induction!
The idea behind inductive proofs is similar to a staircase, as the only way to reach the top is to climb all the steps before it, as noted by Math Bits. The same thing is happening with recursion – each step is generated from the step or steps preceding.

Staircase Analogy
Recursive Formulas For Sequences
Alright, so as we’ve just noted, a recursive sequence is a sequence in which terms are defined using one or more previous terms along with an initial condition. And the most classic recursive formula is the Fibonacci sequence.
The Fibonacci sequence is as follows: 0, 1, 1, 2, 3, 5, 8, 13, 21,…
Notice that each number in the sequence is the sum of the two numbers that precede it. For example, 13 is the sum of 5 and 8 which are the two preceding terms.
In fact, the flowering of a sunflower, the shape of galaxies and hurricanes, the arrangements of leaves on plant stems, and even molecular DNA all follow the Fibonacci sequence which when each number in the sequence is drawn as a rectangular width creates a spiral.
Isn’t it amazing to think that math can be observed all around us?
But, sometimes using a recursive formula can be a bit tedious, as we continually must rely on the preceding terms in order to generate the next.
So now, let’s turn our attention to defining sequence explicitly or generally. All this means is that each term in the sequence can be calculated directly, without knowing the previous term’s value.
Example
In this problem,
What we will notice is that patterns start to pop-up as we write out terms of our sequences. And it’s in these patterns that we can discover the properties of recursively defined and explicitly defined sequences.
We want to remind ourselves of some important sequences and summations from Precalculus, such as Arithmetic and Geometric sequences and series, that will help us discover these patterns.

Arithmetic Sequence Formula

Geometric Sequence Formula

Summation Sequence Formulas
Armed with these summation formulas and techniques, we will begin to generate recursive formulas and closed formulas for other sequences with similar patterns and structures.
Example
So, using our known sequences, let’s find a recursive definition for the sequence 4,9,14,19,24,29,…
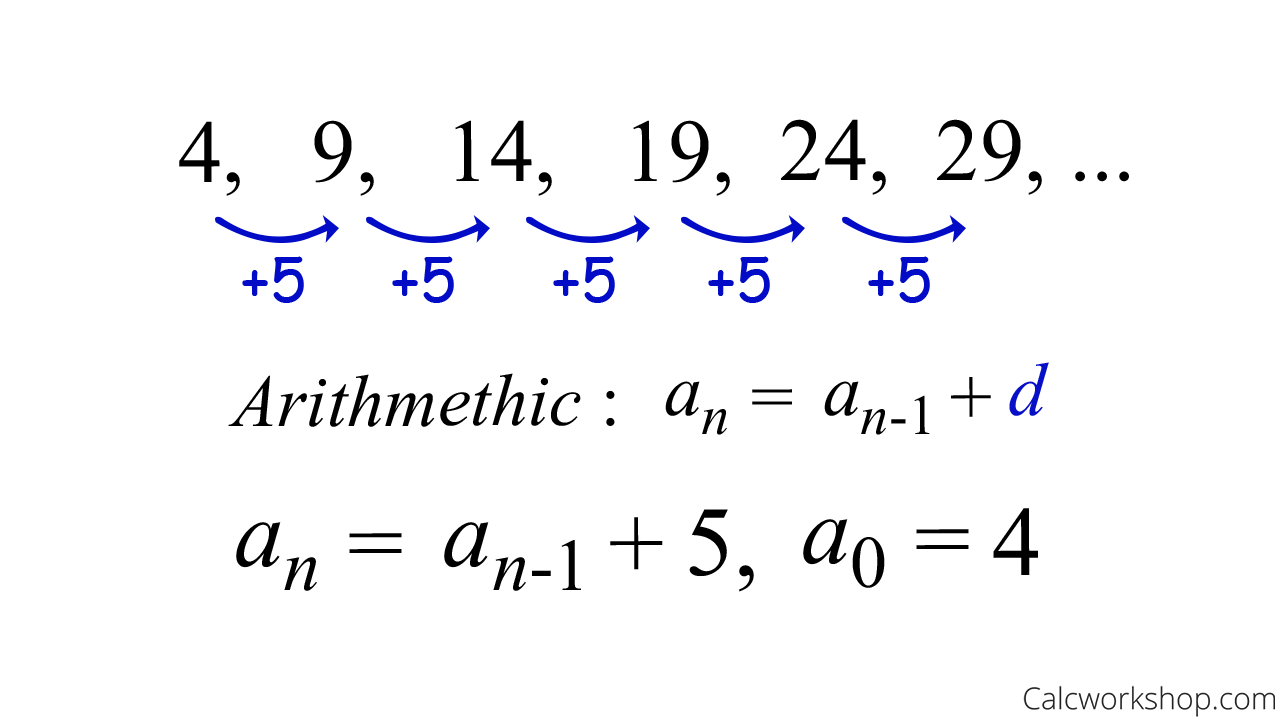
Arithmetic Recursive — Example
Now, using our known summation formulae, let’s find a closed definition for the same sequence of 4,9,14,19,24,29,…
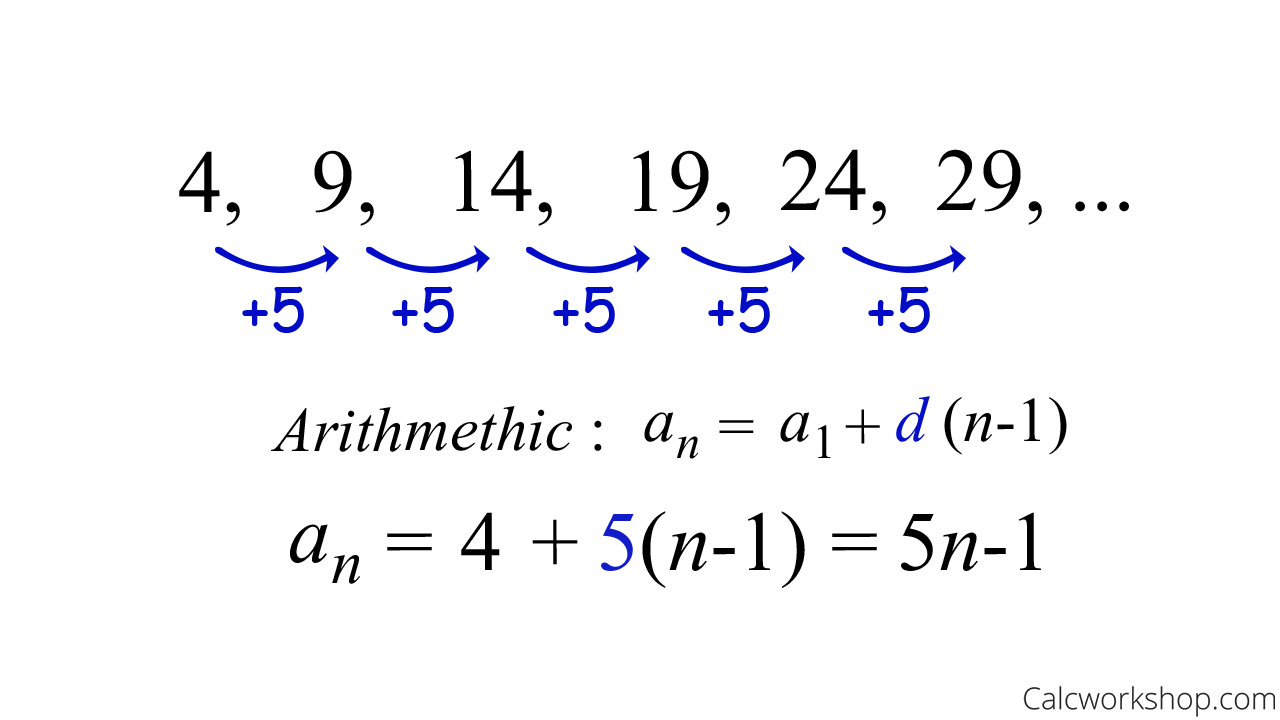
Closed Form Arithmetic Sequence
Additionally, we will discover a superb procedure for finding the sum of an Arithmetic and Geometric sequence, using Gauss’s discovery of reverse-add and multiply-shift-subtract, respectively.
Example
Suppose we wanted to find the sum of the following sequence: 1,3,5,7,9,..,39.
First, we need to find the closed formula for this arithmetic sequence. To do this, we need to identify the common difference which is the amount that is being added to each term that will generate the next term in the sequence. The easiest way to find it is to subtract two adjacent terms. So, for our current example, if we subtract any two adjacent terms we will notice that the common difference is 2.
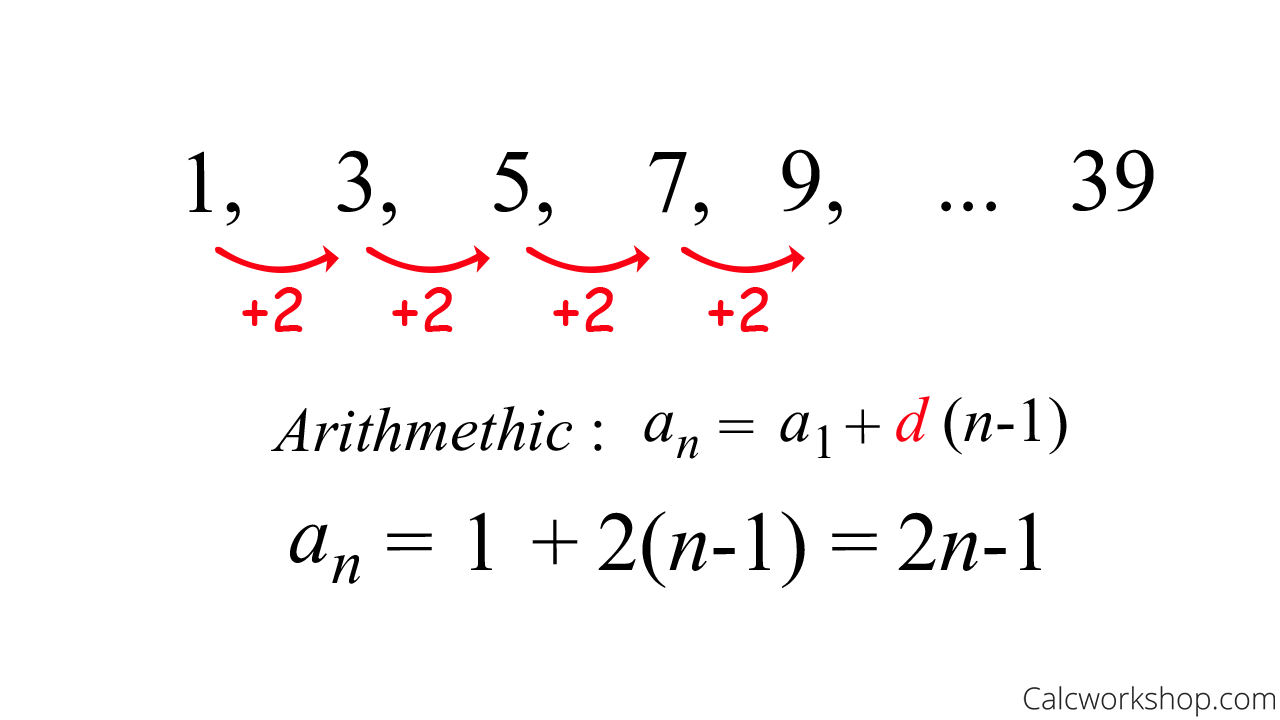
Find Closed Form Of Arithmetic Sequence
Now, we can use the explicit formula to determine the number of terms that we are summing.
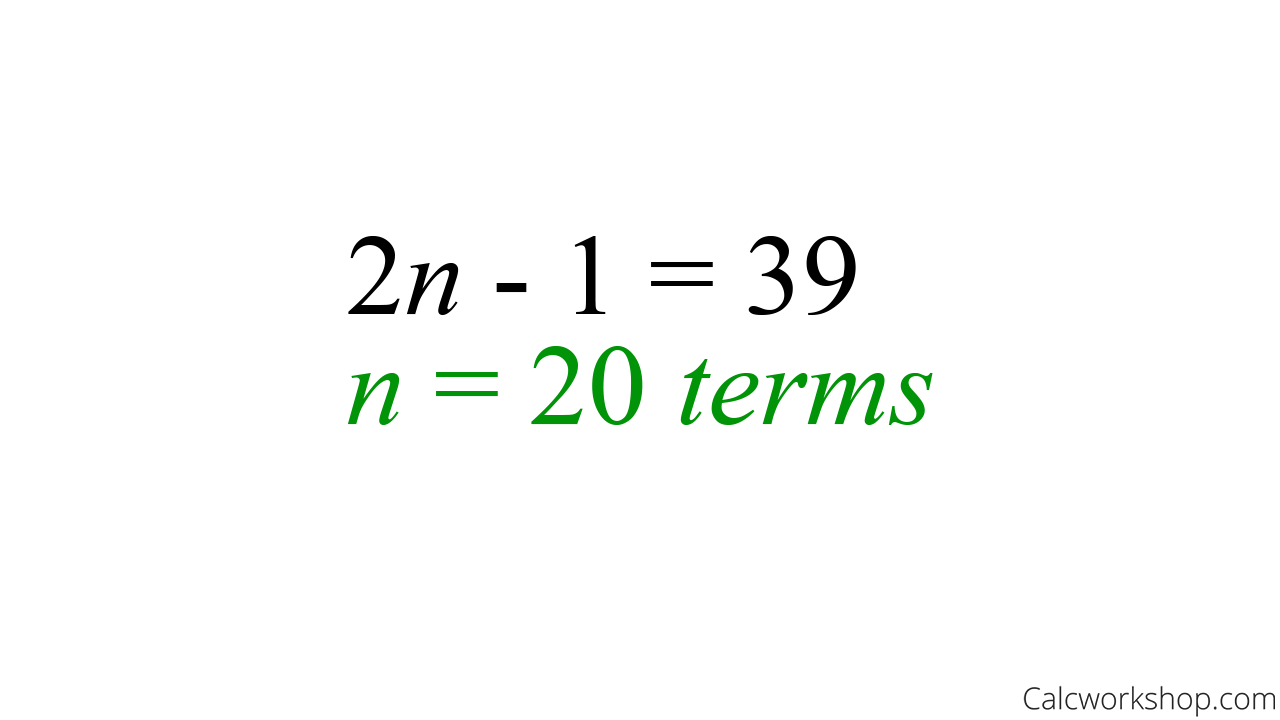
Determine The Number Of Terms In Arithmetic Series
Finally, we apply the reverse and add method to find the sum, where we first list all the terms in one direction, then reverse and list all the terms in the opposite direction. In other words, we will “wrap” the series back onto itself, as MathBitsNotebook nicely states.
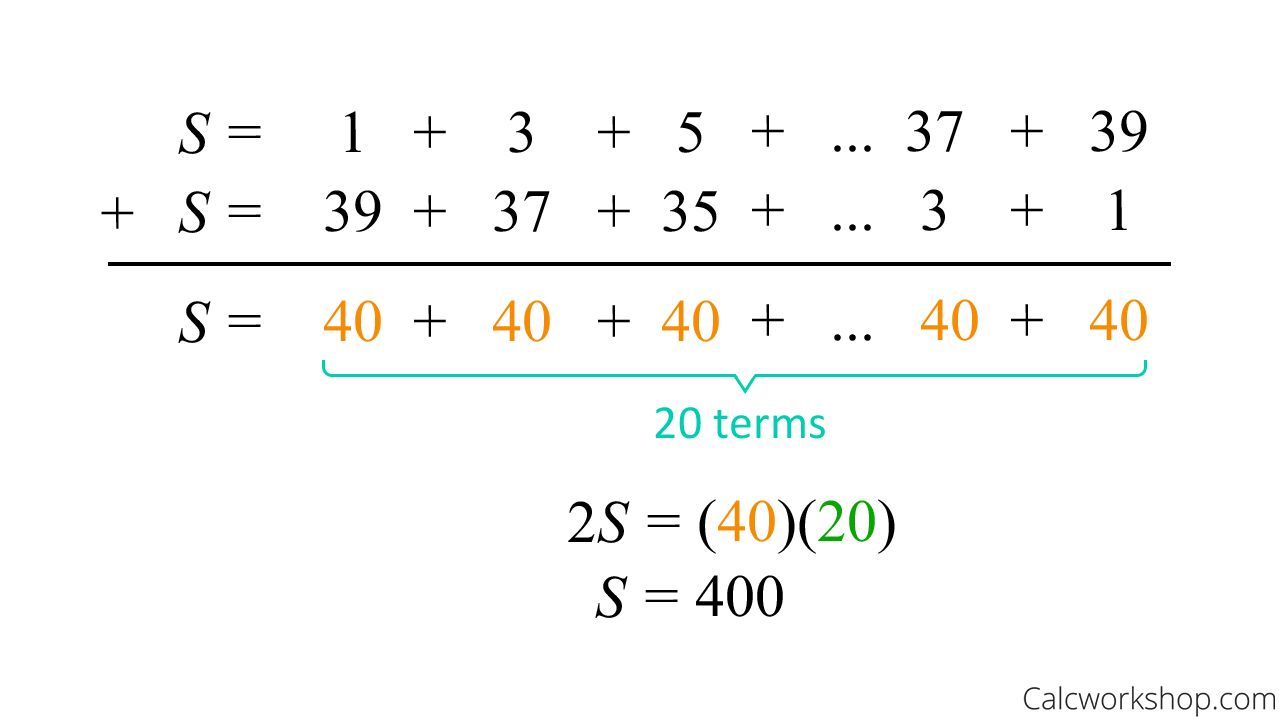
Gauss Method Sum
Summary
Throughout this video, we will see how a recursive formula calculates each term based on the previous term’s value, so it takes a bit more effort to generate the sequence. In contrast, an explicit formula directly calculates each term in the sequence and quickly finds a specific term.
Both formulas, along with summation techniques, are invaluable to the study of counting and recurrence relations. And with these new methods, we will not only be able to develop recursive formulas for specific sequences, but we will be on our way to solving recurrence relations!
So, let’s jump right in and discover the fun!
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 49 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.