Wouldn’t it be nice to have a systematic way of solving recurrence relations that didn’t rely on guess-and-check or iteration?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Well, linear homogeneous recurrence relations are such a class of recurrence relations where we can use a structured, systematic process!
But first, we need to understand what linear homogeneous means as well as degree.
So, a linear homogeneous recurrence relation of degree k with constant coefficients is a recurrence relation of the form:
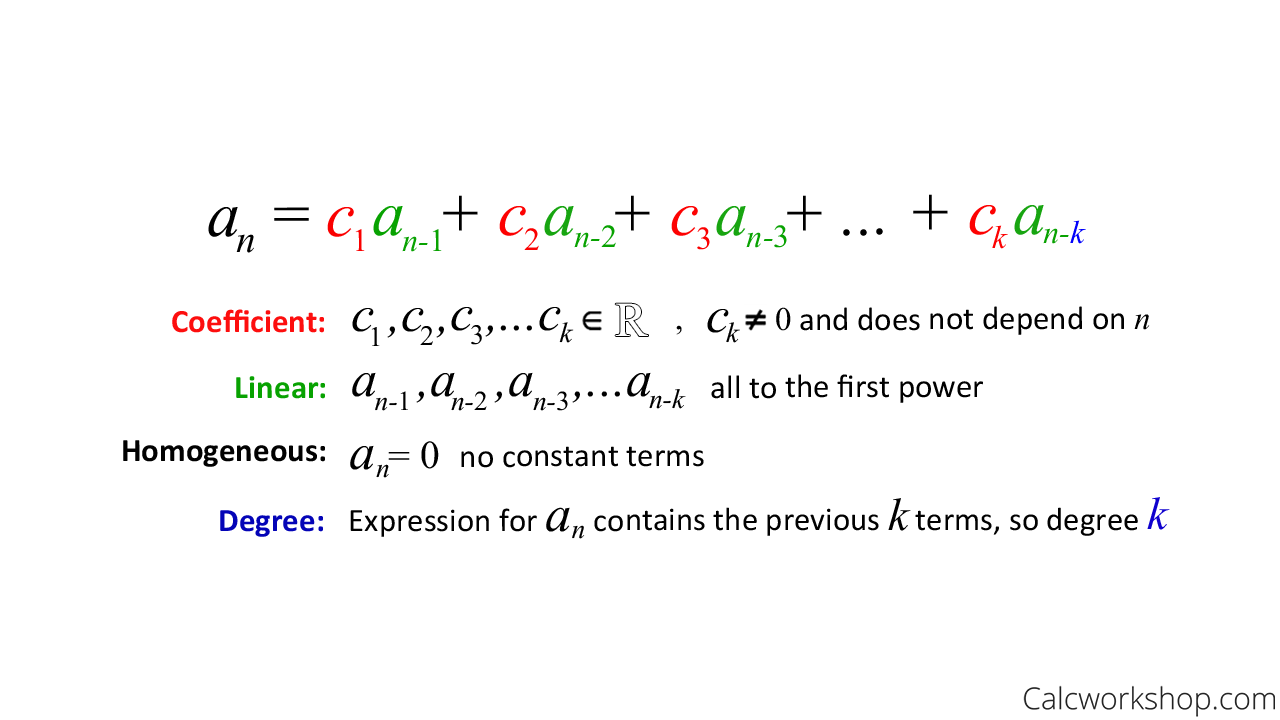
Linear Homogeneous Recurrence Relations Formula
This means that the recurrence relation is linear because the right-hand side is a sum of previous terms of the sequence, each multiplied by a function of n. Additionally, all the coefficients of each term are constant.
And the recurrence relation is homogenous because there are no terms that are multiples of previous terms. All this means is that there are no constant terms.
Additionally, the degree of the recurrence relation is k.
Alright, so now it’s time to practice and make sure we can determine if a recurrence relation fits our special class. The table below shows examples of recurrence relations where we identify if they are linear, homogeneous, and their degree.
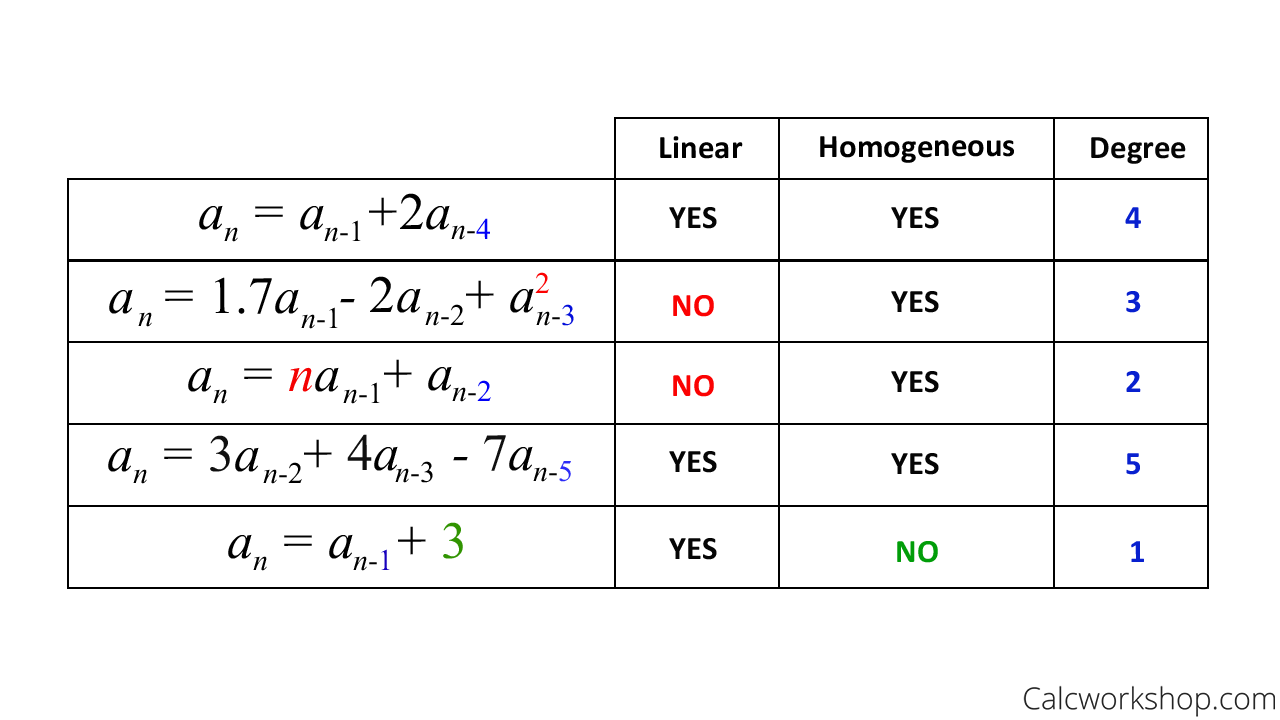
Identify Linear Homogeneous Degree
Okay, so now we’re ready to solve linear homogeneous recurrence relations using the Characteristic Root Method.
The characteristic root method is a way for us to identify solutions of the form of a geometric sequence quickly, as the definition below nicely highlights.
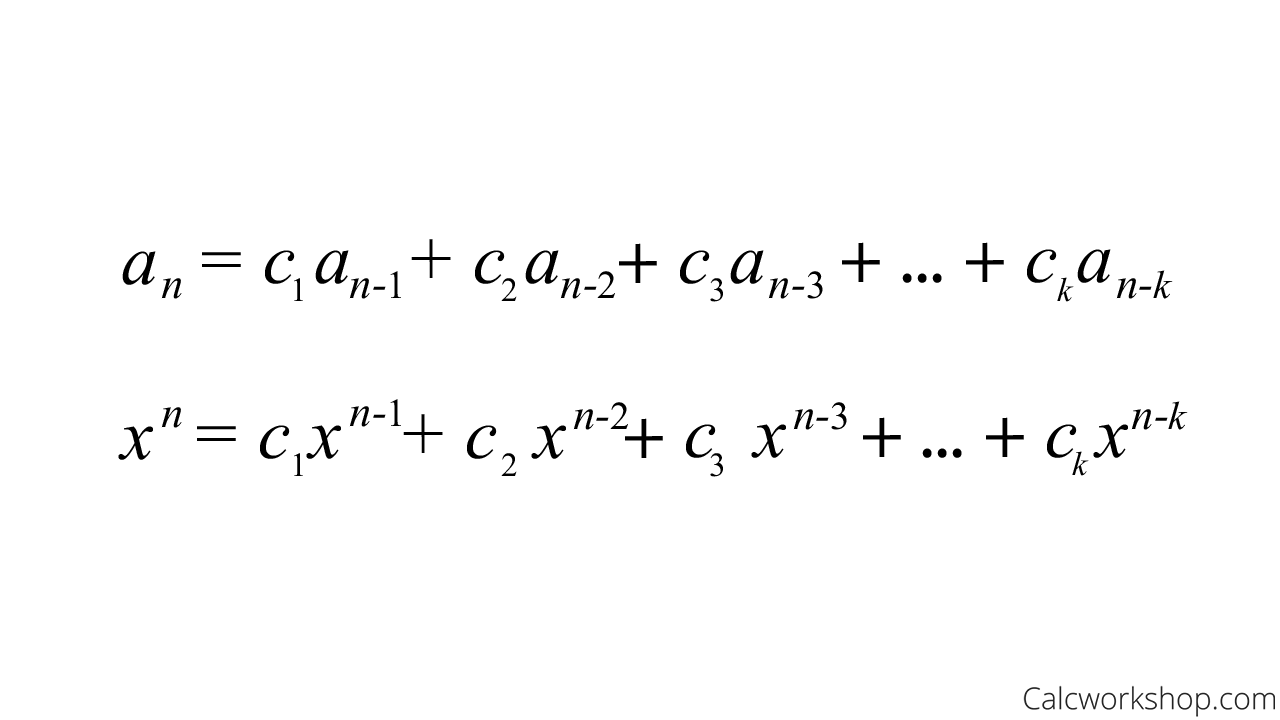
Characteristic Root Definition
Now, if we move all the terms to the left-hand side and set the question equal to zero, we create an equation where the sequence has a solution. In fact, this equation, as shown below, is called the characteristic equation, or the auxiliary equation, and the solutions obtained are called the characteristic roots of the recurrence relation.

Formula For Characteristic Equation
So, the steps for solving a linear homogeneous recurrence relation are as follows:
- Create the characteristic equation by moving every term to the left-hand side, set equal to zero.
- Solve the polynomial by factoring or the quadratic formula.
- Determine the form for each solution: distinct roots, repeated roots, or complex roots.
- Use initial conditions to find coefficients using systems of equations or matrices.
But what are these distinct roots, repeated roots, or complex roots?
These are the types of solutions you can get when solving a polynomial equation, and they relate to the type of closed-form or general formula we will generate for our recurrence relation.

Distinct Real Vs Repeated Real Vs Complex
Please note that most Discrete Math I courses focus on distinct and repeated roots only and leave complex roots for a Discrete Math II course. In this lesson, we will look at all three, so you are well versed in all solving techniques, regardless of the class you are currently enrolled in.
Also, I would like to point out that this should be extremely familiar for anyone who has taken Differential Equations. And for anyone planning on taking Differential Equations in the future, a similar technique will be used again when solving higher order differential equations.
Okay, so let’s see this process in action by walking through a few examples of solving the recurrence relation using the characteristic root method.
Example
We are asked to solve the recurrence relation using the characteristic root method.

Solve Degree Two Recurrence Relation

Solve Degree Two Characteristic Equation
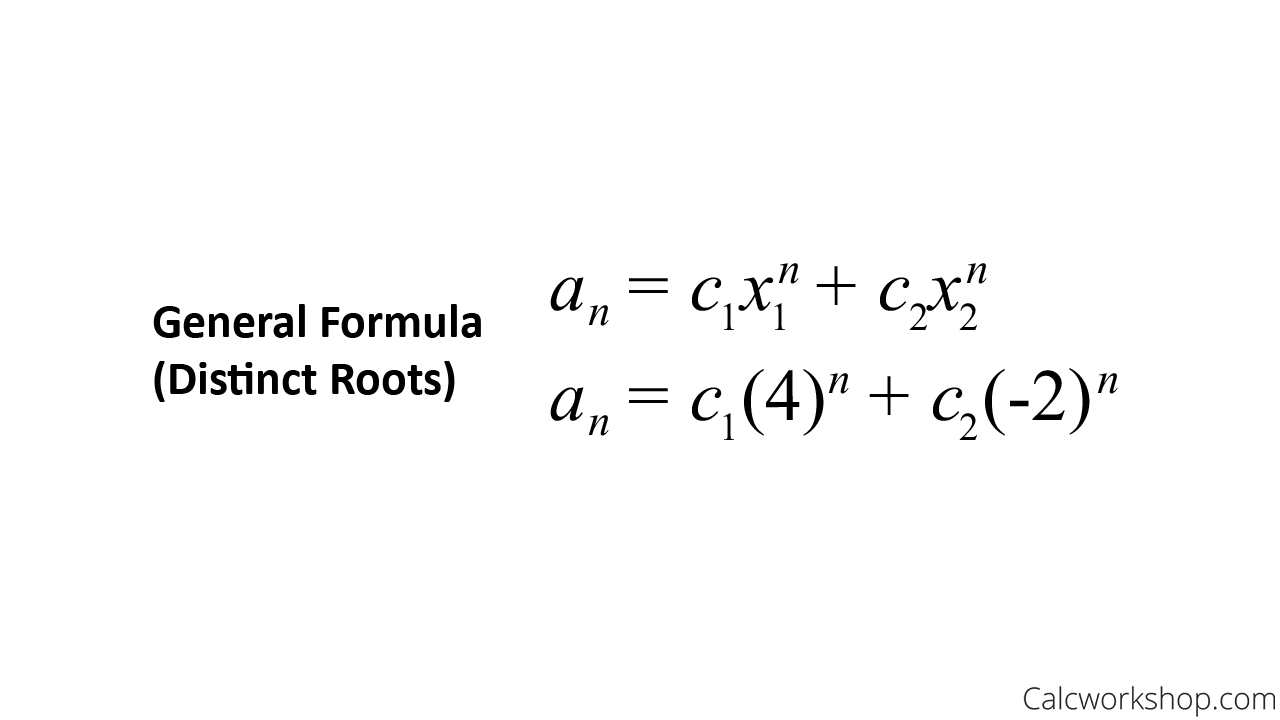
Solve Degree Two Distinct Formula

Solve Degree Two Coefficients

Solve Degree Two Recurrence Closed Form
Example
Now that we’ve seen an example of how to handle distinct roots let’s investigate a recurrence relation with repeated roots.

Recurrence Relation Example

Repeated Root Characteristic Equation

Repeated Root Formula

Repeated Root Formula

Repeated Root Closed Form
Together we will work through numerous examples of solving recurrence relations using the auxiliary equation involving distinct, repeated, and complex roots.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 0 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.