Did you know that order matters when dealing with permutations?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
What Is A Permutation
In fact, a permutation is an ordered arrangement of a set of distinct objects. All this means is that Permutation indicates Placement.
But before we can talk about placement, we need to know that all permutations are grounded in the fundamental counting principle.
Simply put, the counting principle, or product rule for counting, states that if there are p ways to finish a task and q ways to complete another task, then there are pq ways to do both.
But this means there are two possible types of permutations (ways to order objects), and they depend on whether repetition is allowed or whether repetition is not allowed.
Let’s suppose there are n objects and we r ways to order them, then:

Permutation Formula
So, what this indicates is that when we aren’t allowed repetition, we must reduce the number of ways (choices) to arrange the objects.
Basic Example
Let’s look at a few examples so we can get a better understanding of how permutations work.
Let’s suppose you have 5 pictures, and you want to arrange 3 of them on your wall. How many different arrangements can be made?
Let’s say the 5 pictures are labeled A, B, C, D, and E for ease of purpose. This means we can arrange the three images: ABC or ABD or ABE or BCA or CDE, and so on.
This means each of the five photos can be in first, second, or third place on the wall. But what can’t happen is something like this: AAA or BBB or ABA, etc., because once we hang picture A on the wall, we can’t hang it somewhere else as it’s already been used. This implies that repetition is not allowed, and placement (order) matters.
So, for the first spot on the wall, there are 5 possible pictures to choose from (A, B, C, D, E). Let’s say A is the picture that you choose.
The second spot on the wall has 4 choices (B, C, D, E), as picture A has already been hung. Let’s let D be chosen.
And our third and final spot on the wall has 3 choices (B, D, E) as pictures A and D have now been hung up.
So, the total number of picture arrangements given 5 pictures for 3 spots is 5*4*3 = 60.
Permutation Notation
Do you realize that you just used permutations?
Let’s write our problem using mathematical notation. We can write our problem as follows:

Permutation Problems
Cool, huh?
Example
Okay, so now let’s suppose we are given the word GRAM, and we are asked to find the number of arrangements that can be made (they don’t have to spell a word) from the letters in the word GRAM if repetition is allowed.
With Repetition
Well, there are 4 letters in the word GRAM so that means, if we wanted to, we could say GGGG or RRRR or AMAM.
You get the idea.
This means we are dealing with an r-permutation with repetition, so we would say there are 4*4*4*4=256 possible 4-letter arrangements.
Without Repetition
Now, let’s assume repetition is not allowed.
This would mean that if we wanted to construct a 4-letter word only using the letters from the word GRAM, we have 4 choices for the first letter, but once it’s used, we can’t choose it again, so that leaves 3 options for the second letter and 2 choices for the third and 1 choice for the fourth.
In other words, the number of 4-letter arrangements without repetition using the letters from the word GRAM is 4*3*2*1 = 24.
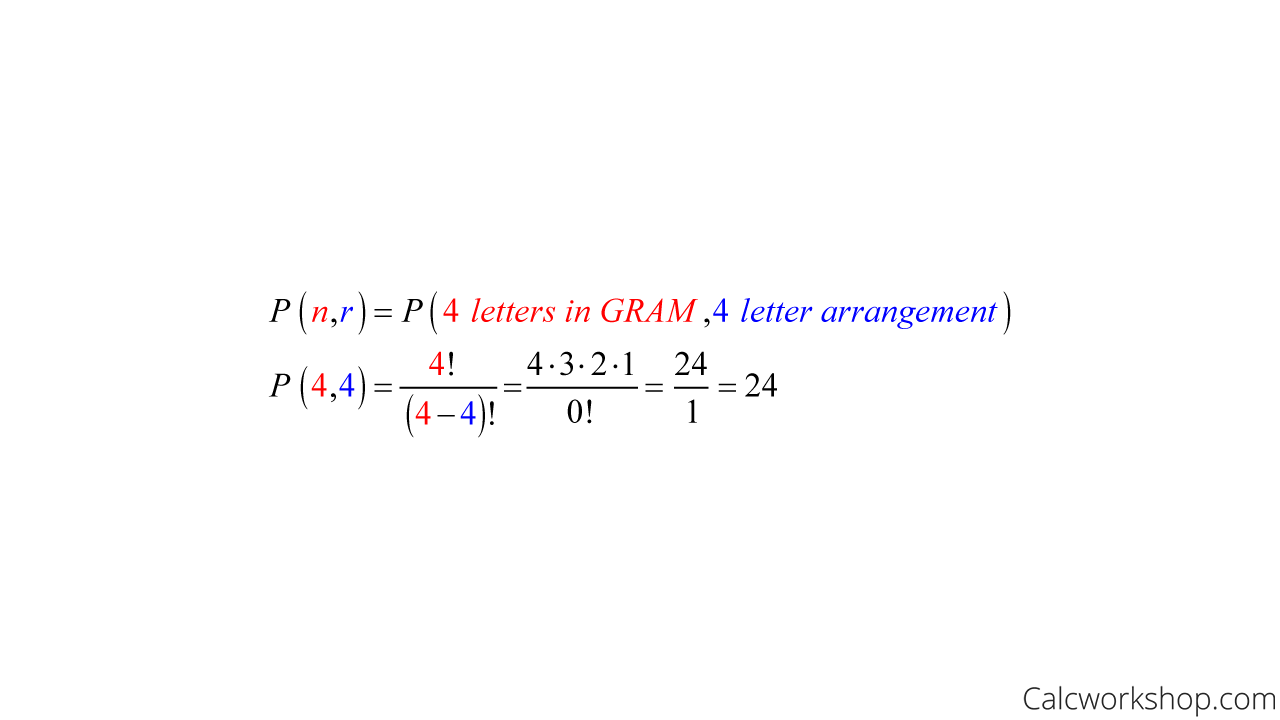
Distinct Permutation Formula
Once again, we used permutations! In essence, we found the number of distinguishable permutations for the word GRAM.
Not bad!
Example
But now, let’s change things up a bit. Let’s suppose we wanted to know how many distinguishable permutations there are of the word GRAMMAR.
Notice that this is a bit different because some letters are the same, which means they aren’t unique or independent. Therefore, while there are 7 letters in the word GRAMMAR, there are only 4 distinguishable letters: G-R-A-M, as there are two Rs, two As, and 2 Ms.
This means we need a generalized theorem that says:

Permutation Formula With Repetition
Alright, so if GRAMMAR has 7 letters, with 1-G, 2-Rs, 2-As, and 2-Ms, this means the number of distinguishable permutations would be:
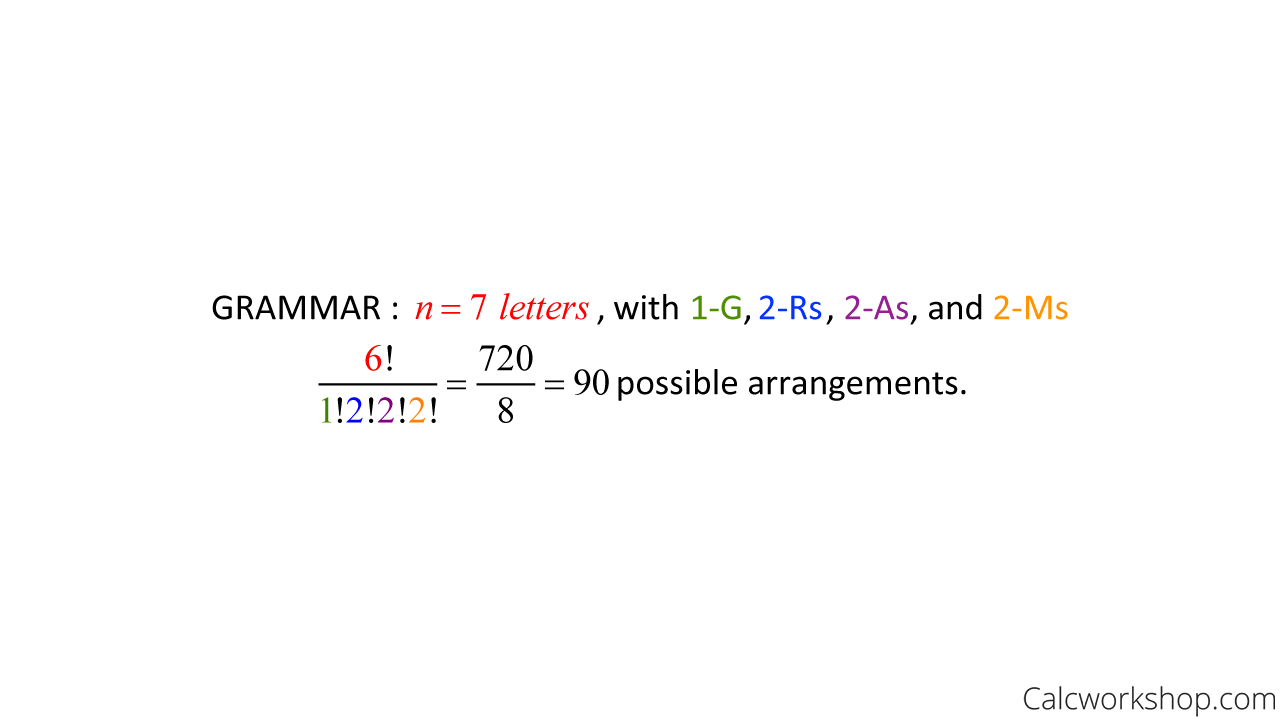
Distinguishable Permutations Example
Awesome!
Circular Permutation
But what happens if we want to arrange people or objects in a circle?
To do this, we need the division rule or the circular rule for permutations.

Circular Permutation Formula
Why?
Example
For example, notice the circle below where Annie (A), Bobbie (B), Carol (C), and Dan (D) are seated.
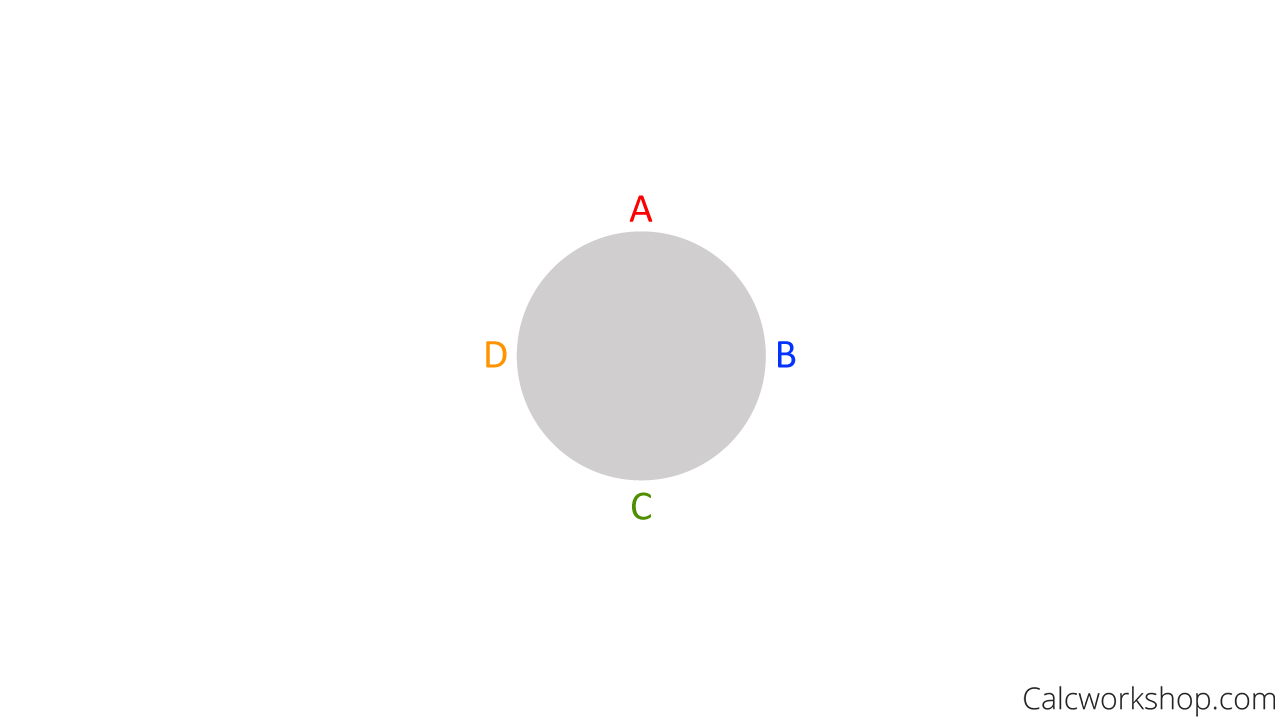
Four People Around Circular Table
But notice that we can easily arrange these four people in different places at the table, but still maintain their order (Annie is next to Bobbie, who is beside Carol, followed by Dan).
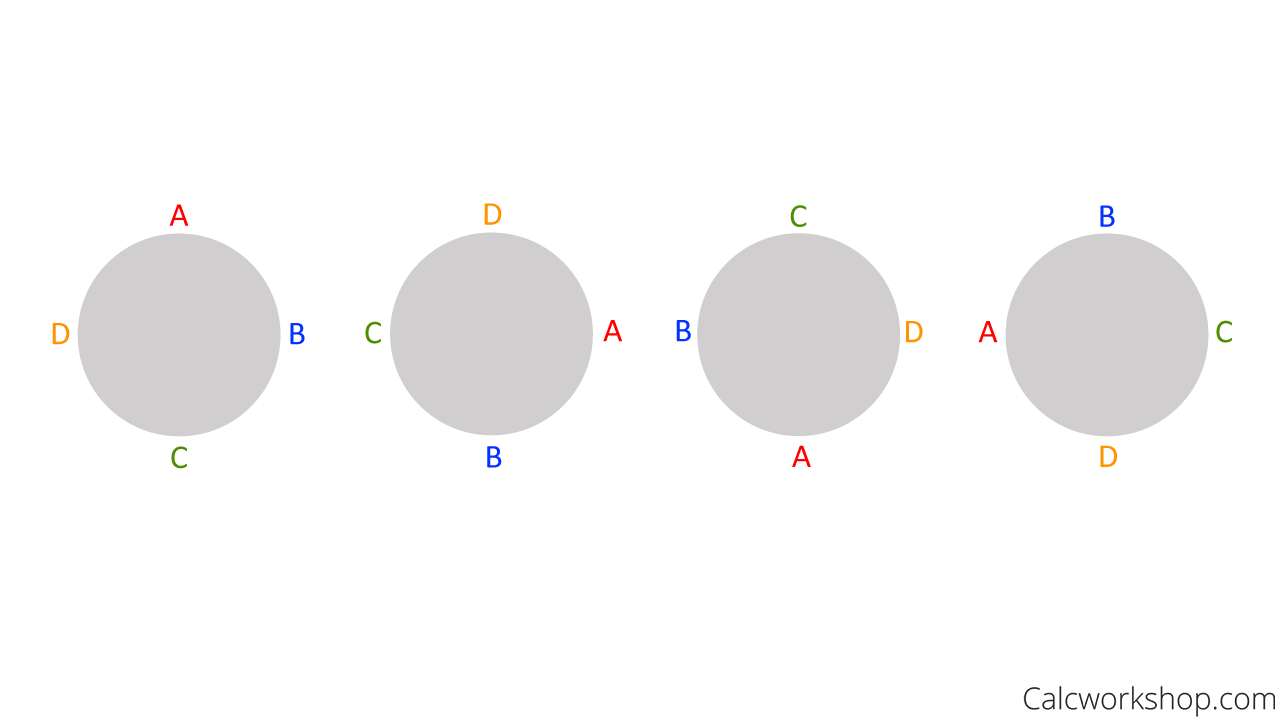
Multiple Arrangements Circular Table
This means we need to divide by the number of repeated arrangements, which is 4. This will ensure that one object (person) is fixed, and the remaining objects (people) are arranged relative to that first object.
So, the number of ways to arrange 4 people around a table is

Circular Permutation Examples
Together we will work through numerous examples, increasing in difficulty as we go, so we make sense of arranging elements in order.
Let’s get to it.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
1 hr 16 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.