Iteration Method Recurrence (How To w/ 7+ Step-by-Step Examples!)

Is there a way to transform a recursively defined sequence into an explicitly defined sequence?

Jenn (B.S., M.Ed.) of Calcworkshop® teaching recurrence relations

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

Yes!

Through iteration.

In our previous lesson, we learned that we could specify an array of numbers recursively or explicitly, and we investigated some essential formulas and summations as they help us in defining sequences.

But if you remember, we had to do a lot of “guess and check” to see if our answer was valid.

Our goal in this lesson is to solve a recurrence relation for a closed-form solution using iteration, also known as backtracking, that helps eliminate most of the guesswork.

The idea behind this method is to substitute terms of the sequence by expanding, or iterating, the recurrence relation as a sum of terms dependent on n and the initial condition. We do this by working backward from the last term.

Example

It’s best to see this in action, so let’s look at an example together where we are given a recurrence relation and initial condition.

It is our job to solve the recurrence relation using iteration.

Recursively Definition — Example

First, we will generate a few terms to help establish the general impression of the sequence.

Partial Term Sequence

Next, we will backward substitute into our recurrence relation until we see a pattern.

Recursive Backtracking

Finally, you’ll quickly begin to notice that the exponent on the six and the subscript value for a are the same!

This means we can generalize a sum of terms that is dependent on n only.

And that is how we use iteration, or backtracking, to solve recurrence relations.

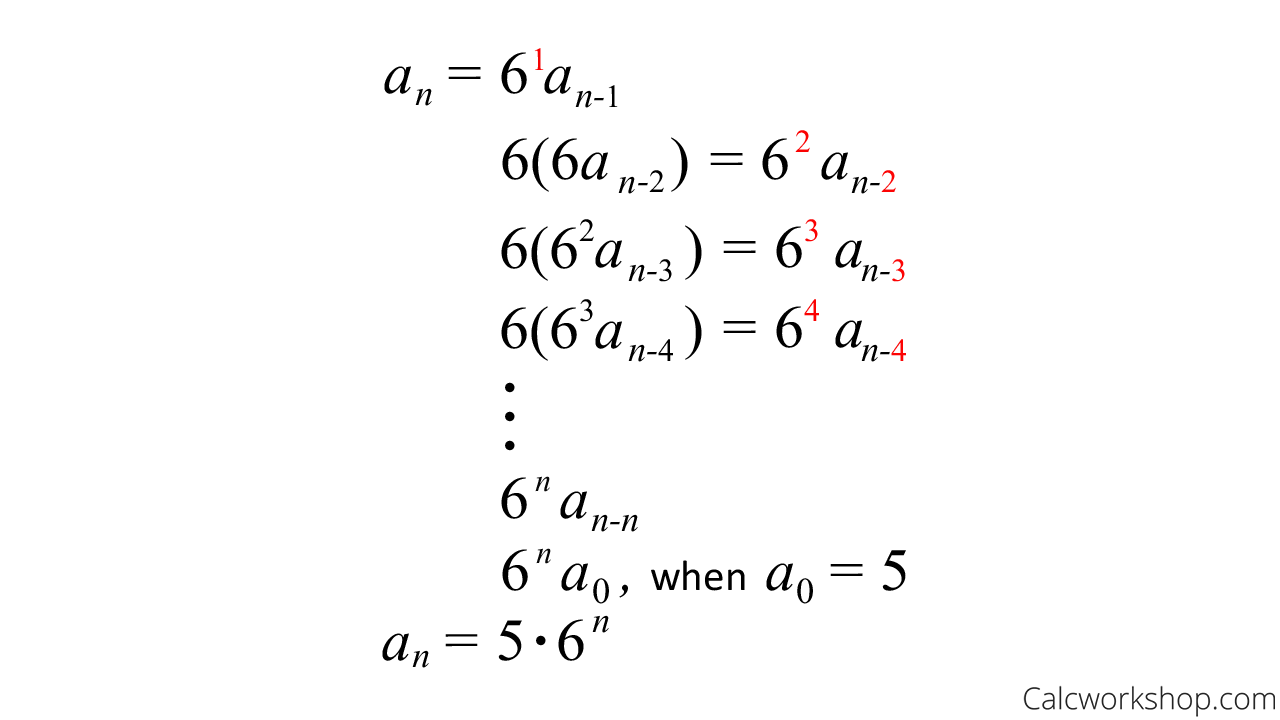
Iteration Closed Form — Example

Together we will work through countless examples in detail. We will use iteration and our summation techniques as well as our rules for geometric series, summation for factorials and exponents, and even algebraic sequences to help us solve more challenging recurrence relations and find closed-form solution.

Let’s get to it.

Video Tutorial w/ Full Lesson & Detailed Examples

1 hr 39 min

Introduction to Video: Recurrence Relations — Iteration Method

00:00:46 Overview of how to solve a recurrence relation using backtracking iterations

00:14:25 Use iteration to solve for the explicit formula (Examples #1-2)

00:30:16 Use backward substitution to solve the recurrence relation (Examples #3-4)

00:54:07 Solve the recurrence relation using iteration and known summations (Examples #5-6)

01:17:03 Find the closed formula (Examples #7-8)

Practice Problems with Step-by-Step Solutions

Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.