Did you know that there’s a way to determine the total number of possible outcomes for a given situation?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In fact, an entire branch of mathematics is devoted to the study of counting, and it’s called combinatorics. Combinatorics studies combinations, permutations, and enumerations of sets of elements.
While you may have already studied these topics in Algebra, the next three lessons along with the pigeonhole principle and binomial theorem, will highlight fundamental concepts of counting and focus on the more challenging aspects of advanced counting.
In this lesson, we will focus on enumeration, or counting objects or elements, that contain specific properties.
Definition
The Fundamental Counting Principle, sometimes referred to as the fundamental counting rule, is a way to figure out the number of possible outcomes for a given situation.
While there are five basic counting principles: addition, multiplication, subtraction, cardinality (principle of inclusion-exclusion), and division. The one that is most closely associated with the title of “fundamental counting principle” is the multiplication rule, where if there are p ways to do one task and q ways to another task, then there are pxq ways to do both.
Now, in this video we will look at the first four rules and tackle the remaining counting principle in the next few lessons.
Okay, so first, let us discuss two most pivotal concepts for counting:
- Addition Principle
- Multiplication Principle
Addition Principle (Rule of Sum)
The Sum Rule states that if a task can be performed in either two ways, where the two methods cannot be performed simultaneously, then completing the job can be done by the sum of the ways to perform the task.

Rule Of Sums
Example
For instance, suppose a bakery has a selection of 20 different cupcakes, 10 different donuts, and 15 different muffins. If you are to select a tasty treat, how many different choices of sweets can you choose from?
Here’s how this works.
Because we have to choose from either a cupcake or donut or muffin (notice the “OR”), we have 20 + 10 + 15 = 45 treats to choose from.
Multiplication Principle (Rule of Product)
The Product Rule states that if a task can be performed in a sequence of tasks, one after the other, then completing the job can be done by the product of the ways to perform the task as noted by Lumen Learning.

Rule Of Product
Example #1
Continuing our story from above, suppose a bakery has a selection of 20 different cupcakes, 10 different donuts, and 15 different muffins — how many different orders are there?
What makes this question different from the first problem is that we are not asking how many total choices there are. We are asking how many different ways we can select a treat.
It’s possible that you only want one treat, but you can quite easily want more than one.
So how many different orders can you create, if you’re allowed to choose as few or as many as you like?
This is the job for the product rule!
Because we can choose treats from a selection of cupcakes and donuts and muffins (notice the “AND”), we 20 x 10 x 15 = 3,000 ordering options.
Example #2
Now let’s look at another example. Suppose that either a member of the mathematics faculty or a student in the department is chosen as a representative to an oversight committee. How many different choices for this representative are there if there are 37 faculty members and 83 mathematics majors, and no one is both a faculty member and a student. Solution: By the sum rule, it follows that there are 37 + 83 = 120 possible ways to pick a representative.
Remember, the product rule states that if there are p ways to do one task and q ways to another task, then there are pxq ways to do both.
Principle Of Inclusion Exclusion
And this leads us to the Principle of Inclusion-Exclusion (PIE), sometimes called the subtraction rule.

Subtraction Rule Pie
Definition
This rule states that if a task can be done in either p or q ways, the total number of ways to complete the job is p + q minus the number of ways to do the task that are common to both p and q, which alleviates the possibility of double counting.
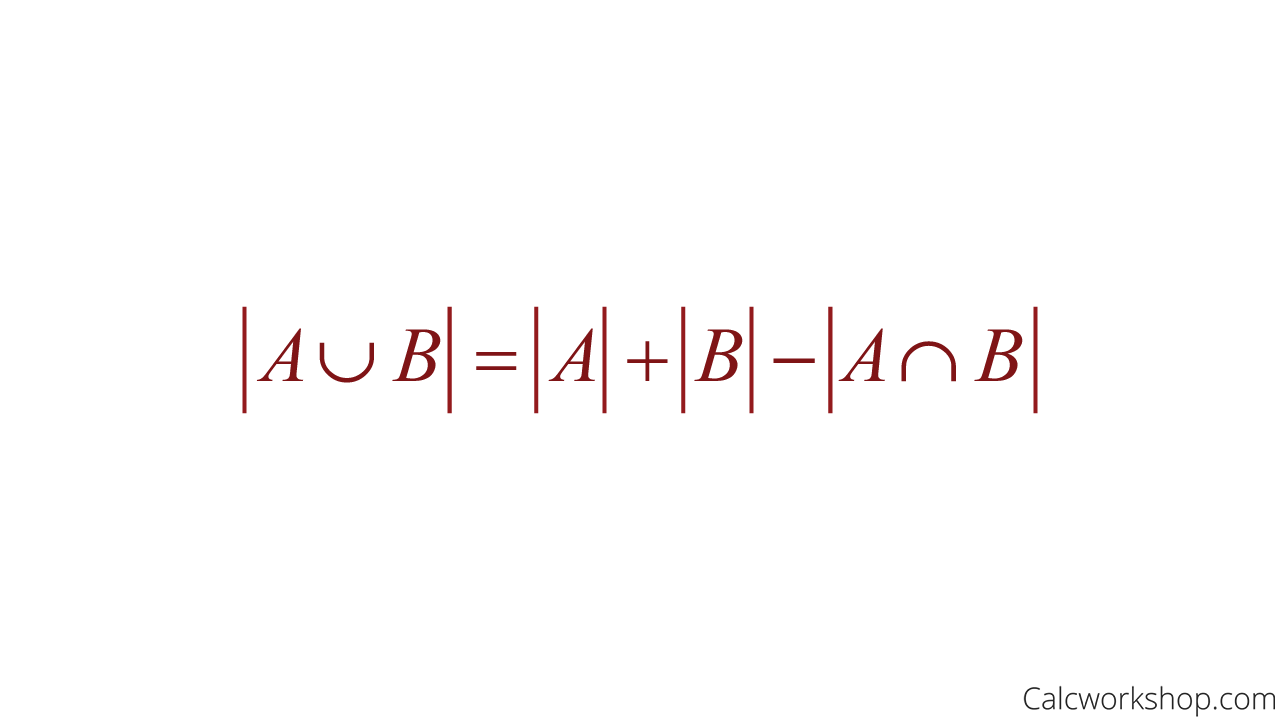
Inclusion Exclusion Formula
Now, we’ve seen all of these ideas before in either previous units such as sets or our study of functions and statistics in Algebra. So, it’s time to combine these concepts to solve more challenging counting problems where we may need to combine all of the counting rules listed above.
Hard Example #1
In this problem, suppose four cards are chosen at random from a standard 52-card deck, with replacement. And we wish to determine the number of four-card sequences where all four cards are from the same suit.
Well, what do we know?
There are four suits in a deck (diamonds, hearts, clubs, spades), which means there are 13 cards in each suit.
And if we want to determine the number of four-card sequences that are all the same suit, then this would mean that we would be looking for either all hearts or all diamonds or all clubs or all spades.

Choose Cards Same Suit — Example
Hence, there are 114244 possibilities!
Hard Example #2
Additionally, what if we were interested in knowing how many integer numbers less than 500 ends with 0?
First, we need to determine how many one-digit numbers are less than 500 and end with 0. Well, there’s only one number (i.e., “0”) that fits that description, so there’s only one possible way to get this value.
Second, we need to think of all the two-digit numbers that are less than 500 and end with 0. Well, for a number to have two digits, the first digit can’t be 0, so that means we are limited to choosing digits ranging from 1-9, and the second digit has to be zero, so there’s only 1 possible value for this.
And finally, we need to think of all the three-digit numbers that are less than 500 and end with zero. Well, for a number to have three digits, the first digit can’t be 0. And secondly, the number has to be less than 500, so the digit must be a value of 4 or less. Therefore, our first digit for this three-digit number ranging from 1-4. Now the second digit can be any value, so that means it can range from 0-9, and our third digit has to be zero, so there’s only 1 possible value for this.

How Many Four Digit Numbers — Example
This means there are 1 + (9)(1) + (4)(10)(1) = 50 different numbers that are less than 500 and end with 0!
Summary?
Together we will look at various examples using advanced techniques involving the counting principle as well as the sum and product rules to ensure understanding of counting principles.
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 17 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.