In mathematics, a combination is the number of possible arrangements of objects or elements from a group when the order of selection doesn’t matter.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In other words, combinations show us how many different possible subsets we can form from the larger set.
For instance, suppose you are going on a five-day vacation where the planned activities are:
- Rock Climbing
- Hiking
- Swimming
- Snorkeling
- Shopping
How many different ways can you arrange these five activities?
Because it doesn’t matter which order you complete these activities, this is no longer a permutation but a combination, because as I like to think of this…
… a Combination is when you Couldn’t Care less about the order — notice they both start with “C.”
Okay, so just like permutations, there are two types of combinations:
- Repetition Allowed.
- Repetition Is Not Permitted.
Without Repetition
Let’s look at the most classic form, combinations without repetition, as noted by University of Pittsburgh.
Simply put, if we let n be the number of items or objects and r represent the number of subgroups we wish to select, then:
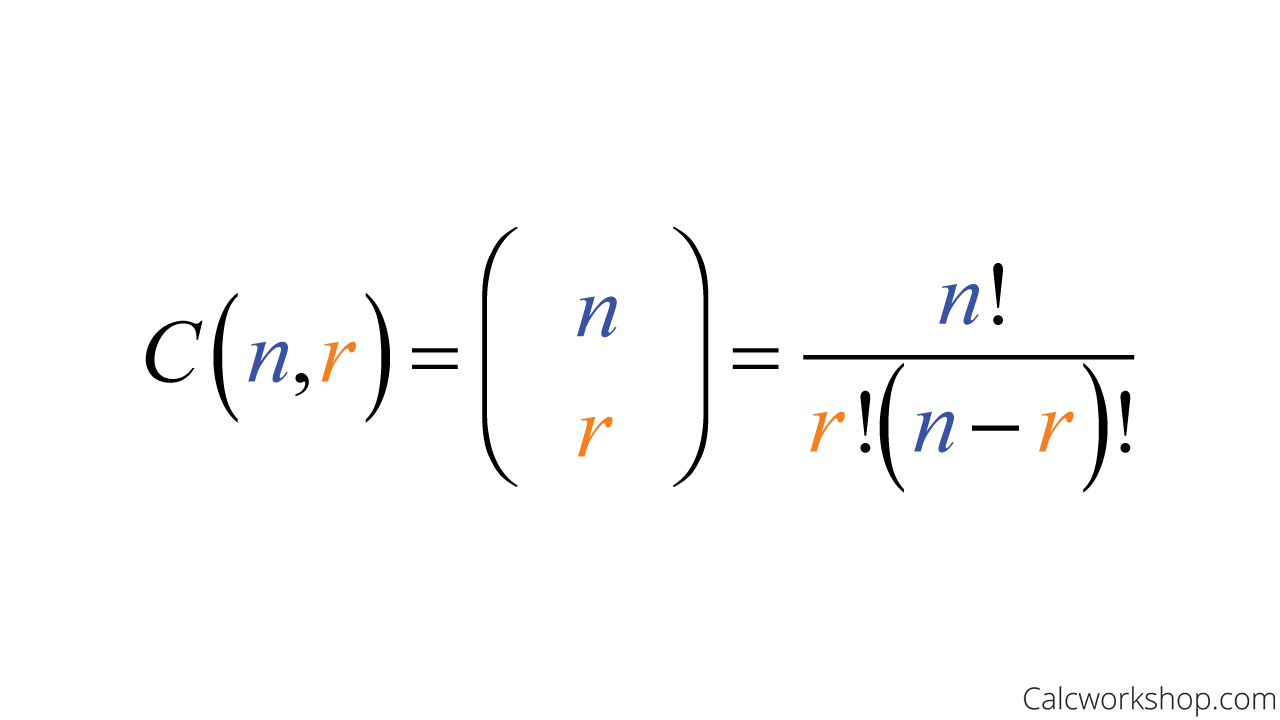
Combination Without Repetition Formula
Example – Deck Of Cards
Suppose you are given a standard deck of 52 cards.
How many different possible hands of 5 cards can be dealt?
Because each card’s order is not important, and because once you deal a card from the deck, you don’t put it back in the deck, we are dealing with an example of combinations without replacement.
If we let n represent the 52 cards and r be the 5 cards hands that are dealt, then:
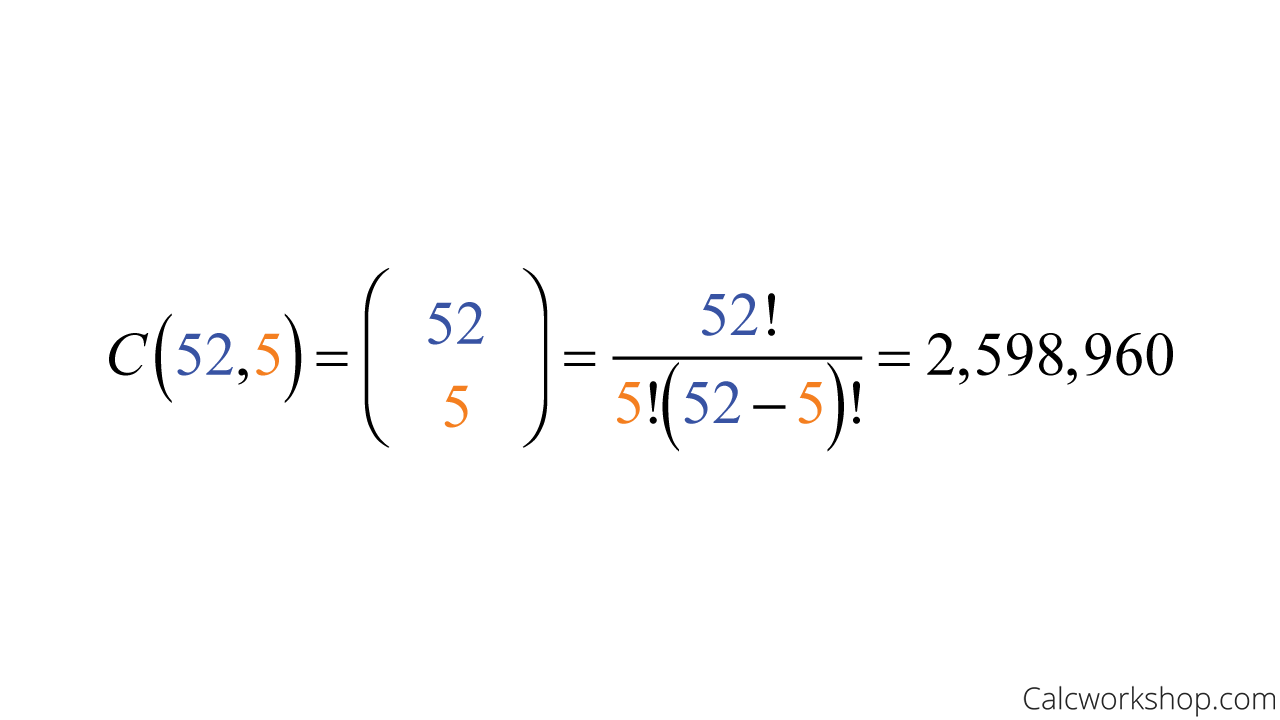
How Many Combinations In A Deck Of Cards
So, there are 2,598,960 possible combinations of 5 card hands that can be dealt with a 52-card deck.
Example – Multiplying Combinations
And combinations can be combined with the fundamental counting principle as if there are m different combinations to perform task one and n different combinations to perform task two. We can blend these combinations using multiplication.
For instance, how many ways can a committee of 3 men and 2 women be chosen from an organization comprised of 10 men and 12 women?
The way we need to think of this is to assume we are choosing a committee of 3 men from the 10 men possible and a committee of 2 women from the 12 women possible. Consequently, we multiply the number of ways that each of these committees can occur as follows:
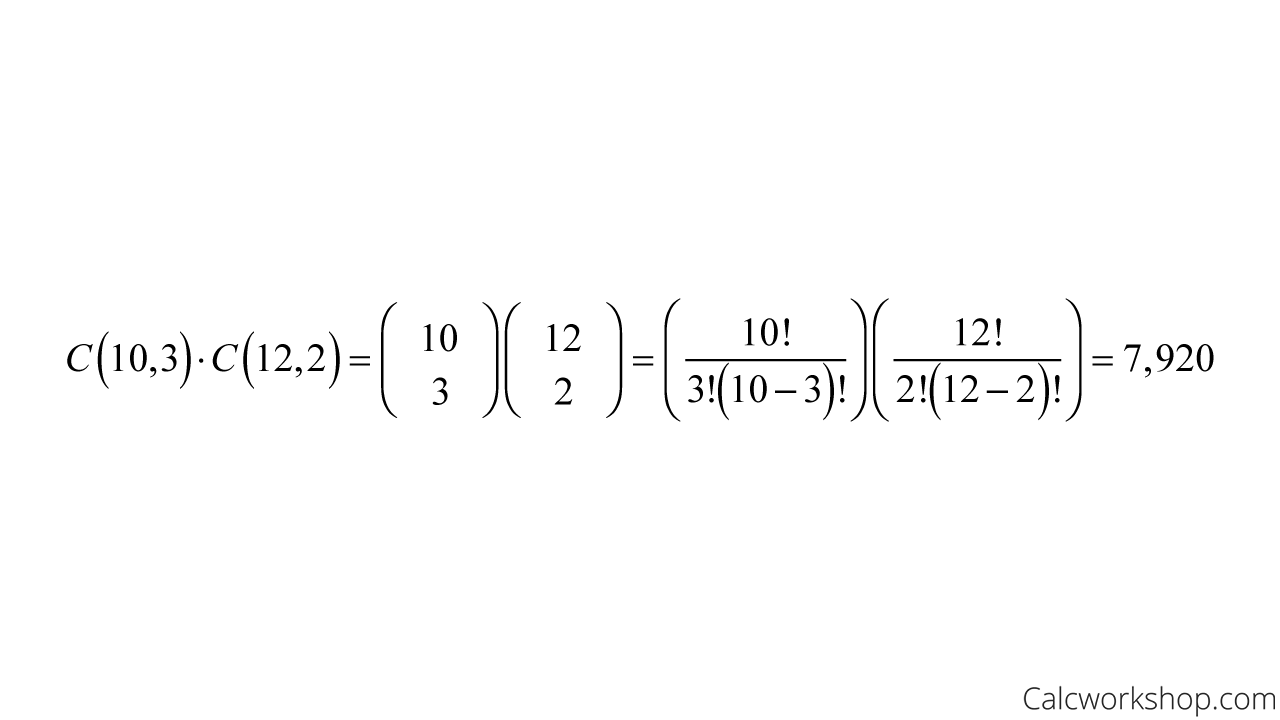
Multiplying Combinations — Example
Repetition Allowed
Now it’s time to look at how we use combinations when repetition is allowed.
Example – Ice Cream
Suppose you walk into an ice-cream shop to buy 5 ice cream cones for you and your four friends.
The store only has 3 different types of ice-cream flavors for sale:
- Chocolate
- Vanilla
- Strawberry
Now, the order doesn’t matter as purchasing a chocolate cone before a vanilla cone won’t make a difference, but we do have a little bit of a problem — how can we choose 5 ice cream cones when there are only 3 possible choices to choose from?
Thankfully, we can use the formula for combinations with repetition, which says the number of combinations of n items taken r at a time with repetition is:
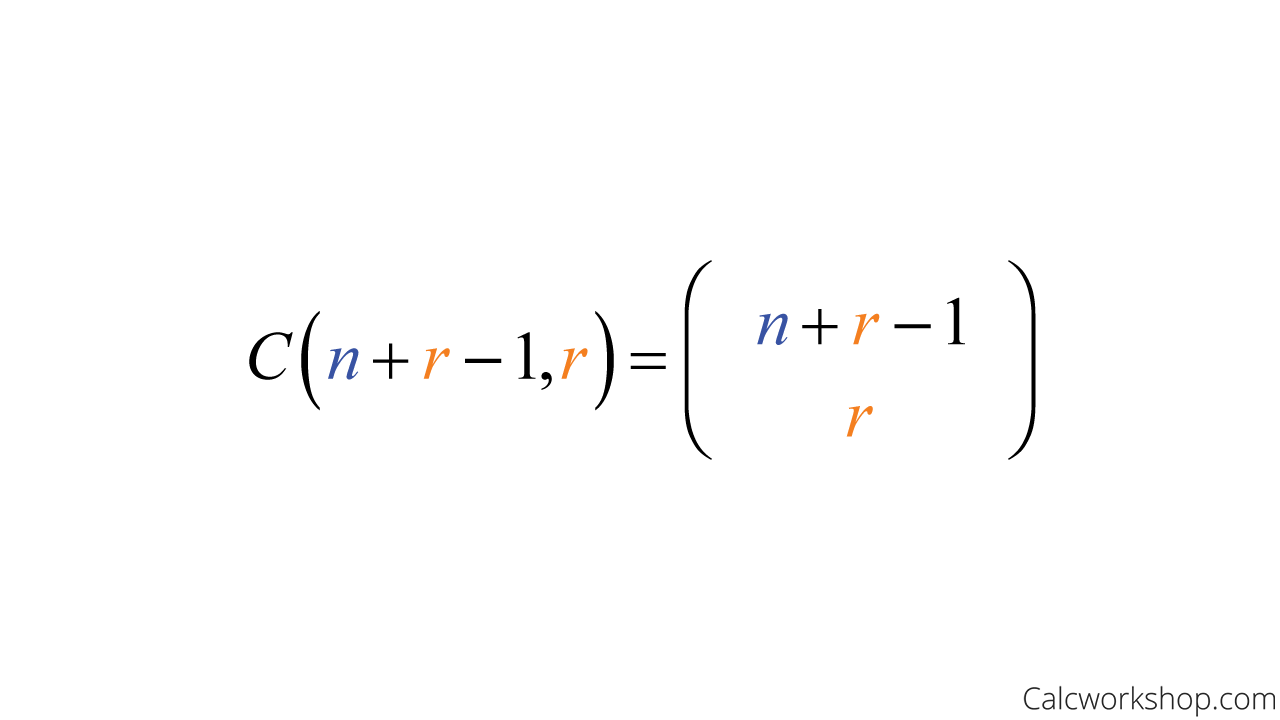
Combination With Repetition Formula
This means, for our ice cream example, if we have n = 3 flavors and r = 5 selections, then the number of ways you can select 5 ice cream cones is:
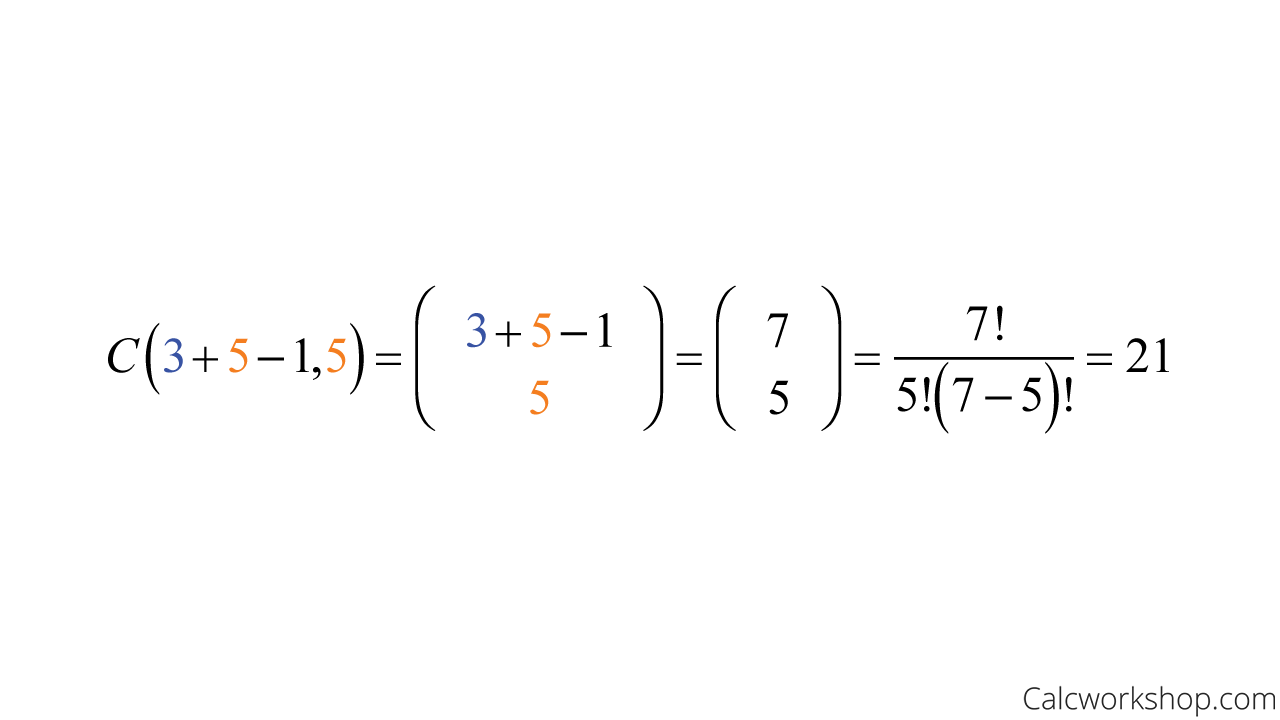
How Many Ways — Combinations Repetition Allowed
Throughout our lesson, we will explore various ways to combine permutations, combinations, and the fundamental counting principle, including the sum-rule, to create multiple arrangements and subgroups for finding combinations with and without repetition.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
1 hr 18 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.