Did you know that combinations, which is the unordered selection of objects, is also called the binomial coefficient?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Yep!
The combinations of n elements taken k at a time without repetition often stated as “n choose k” is equal to the binomial coefficient or the combinatorial number.
What this means is that we quickly find the expanded form of any binomial by applying combinations.
The binomial theorem states that if a and b are variables and n is a nonnegative integer, then:

Binomial Coefficient Formula
Let’s see the binomial theorem in action with the following problem:
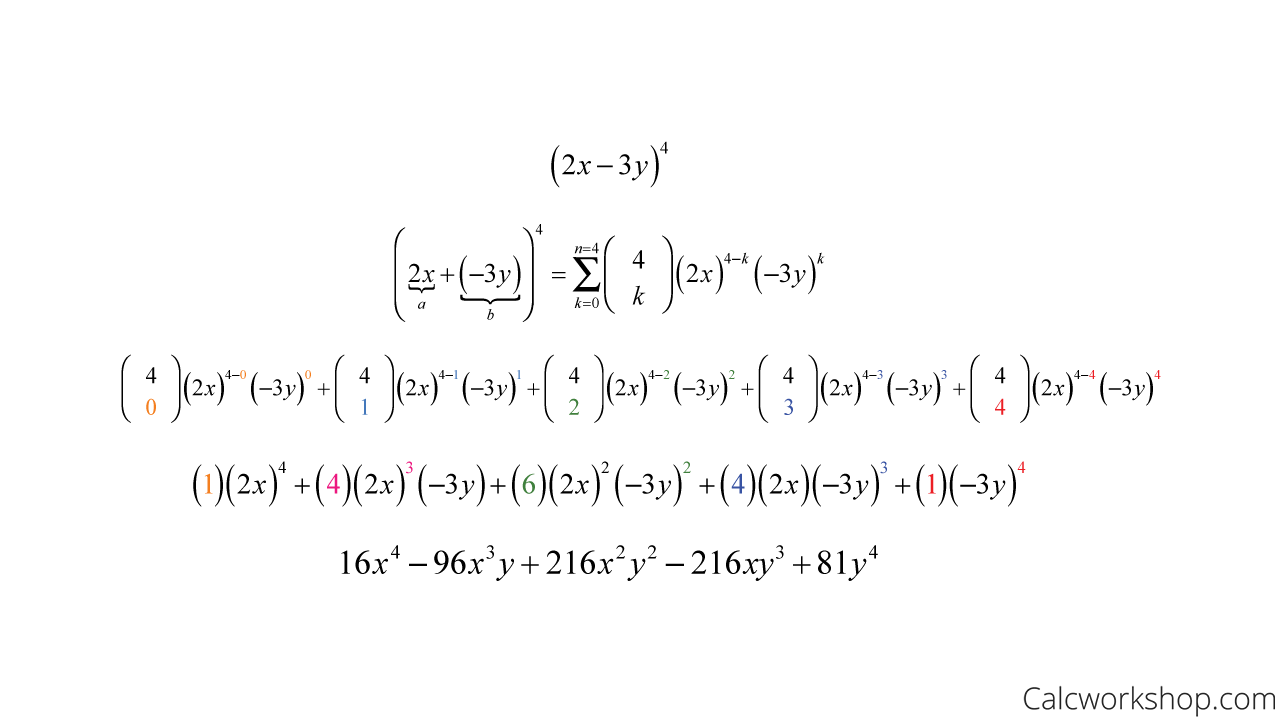
Find The Coefficient Using Binomial Theorem Expanded
Using combinations, we can quickly find the binomial coefficients (i.e., n choose k) for each term in the expansion.
But the real power of the binomial theorem is its ability to quickly find the coefficient of any particular term in the expansions.
Example
For instance, suppose you wanted to find the coefficient of x^5 in the expansion (x+1)^304. All we have to do is apply combinations!

What Is The Coefficient Of The Last Term
Gosh, aren’t you glad you didn’t need to multiply the binomial 304 times just to find that coefficient? Me too!
Together we will look at how to successfully wield this unique “superpower” to find the expansion of such questions as:

N Choose K Problems
Throughout this lesson, we work through various examples and successfully apply the binomial theorem to multiple instances, focusing predominately on more challenging expansions.
We will also see how the binomial coefficient and Pascal’s triangle are efficient and straightforward ways to find indicated coefficients. Additionally, we will use proof by mathematical induction to aid us in deriving formulas for various series while using the binomial coefficient.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
1 hr 34 min
- Introduction to Video: Binomial Coefficients
- 00:00:43 How to use the Binomial Theorem (Example #1)
- Exclusive Content for Members Only
- 00:14:08 Pascal’s Triangle for finding binomial coefficients (Examples #2-3)
- 00:24:56 Find the indicated coefficient for the binomial expansion (Examples #4-5)
- 00:34:26 Find the constant term of the expansion (Examples #6-7)
- 00:46:46 Binomial theorem to find coefficients for the product of a trinomial and binomial (Examples #8-9)
- 01:02:16 Use proof by induction for n choose k to derive formula for k squared (Example #10a-b)
- 01:21:04 Find the integer coefficients and formula for k^2 (Example #10c-d)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.
