Just what is the intersecting secants theorem?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
That’s what today’s geometry lesson is all about.
You’re going to learn how to use this theorem to find missing angles & arc utilizing the relationships between tangents, secants, chords, and arcs.
Let’s get to it!
The intersection of tangents and secants creates three distinct relationships or scenarios. The same is true when two secants or two chords intersect.
The distinguishing characteristic between each case lies in where the intersection happens.
- On A Circle
- Outside A Circle
- Inside A Circle
And in each of these three situations, the lines, angles, and arcs have a special relationship that is illustrated by the Intersecting Secants Theorem.
Case #1 – On A Circle
The first situation is when a tangent and a secant (or chord) intersect on a circle or when two secants (or chords) intersect on a circle.
The diagram below shows what happens when tangents and secants intersect on a circle. You get inscribed angles and arcs! Therefore, the measure of inscribed angle 1 is equal to one-half of the measure its intercepted arc ACB. Likewise, the measure of inscribed angle 2 is equal to one-half its intercepted arc AB.

Tangent Chord Angles
Case #2 – Inside A Circle
Our second possibility is when two secants intersect inside the circle.
The image below highlights case #2 well, by showing how when two secants or chords intersect inside a circle, we find the measure of angles 1 or 2 by taking one-half the sum of the measures of the arcs that are created via vertical angles.
The key to remember is that when two secants or chords intersect inside the circle, you will always add!

Intersecting Chords Angle Measure Theorem
Thankfully, this scenario mimics the Inscribed Angle Theorem, where the inscribed angle is equal to half the intercepted arc, as ck-12 accurately states.
Case #3 – Outside A Circle
And lastly, the third situation is when two secants, or a secant and a tangent, intersect outside the circle.
In this case, there are three possible scenarios, as indicated in the images below. Notice that the exterior angle that is created by the intersection of two secants or tangents is one-half the difference of the major and minor arcs.
Here’s a big hint…
…when two secants or tangents intersect outside the circle, you will always subtract big minus little!
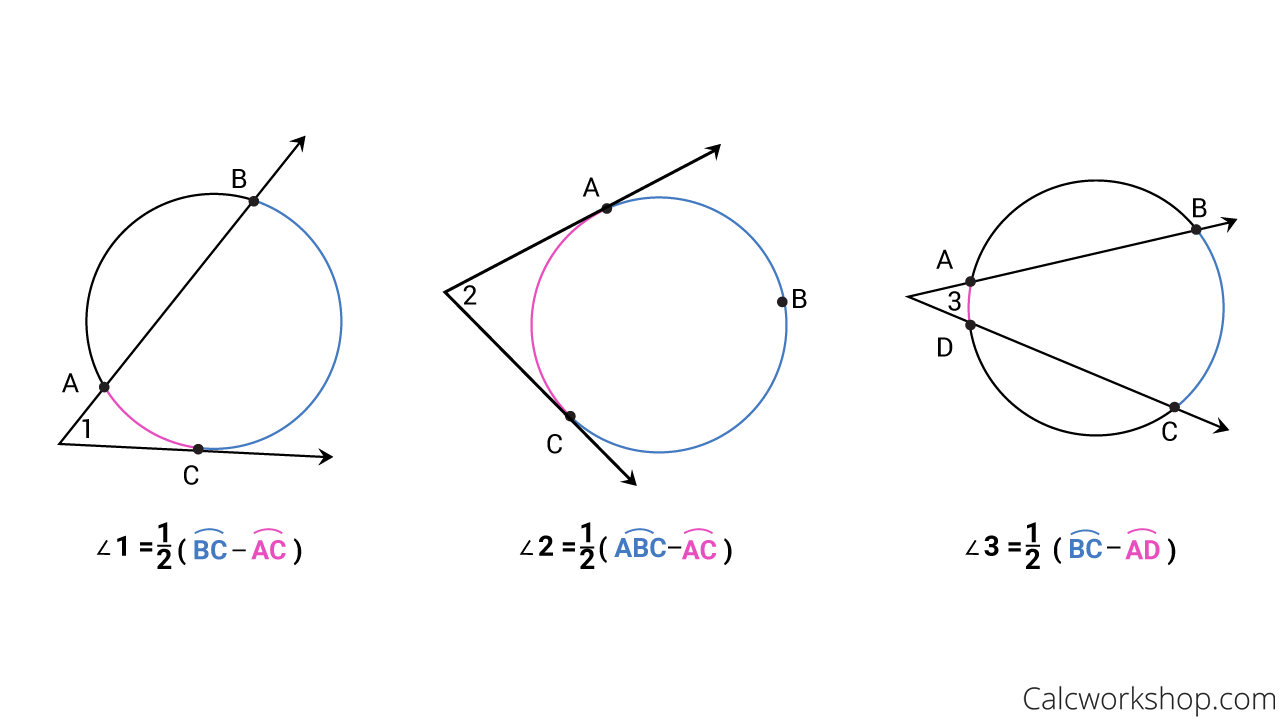
Tangent Secant Exterior Angle Measure Theorem
In the following video, you’re are going to learn how to analyze countless examples, to identify the appropriate scenario given, and then apply the intersecting secant theorem to determine the measure of the indicated angle or arc.
Video – Lesson & Examples
1 hr 4 min
- Introduction to Video: Intersecting Secants
- 00:00:24 – Overview of the four theorems for angle relationships in circles
- Exclusive Content for Member’s Only
- 00:11:17 – Find the indicated angle or arc given two secants or tangent lines (Examples #1-5)
- 00:25:55 – Solve for x given two secants, tangents or chords (Examples #6-11)
- 00:38:56 – Find the measure of the arc or angle given secants and tangents (Examples #12-15)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.