Are the disk and washer methods the only way to find the volume of a solid of revolution?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Absolutely not!
What Is The Shell Method
The shell method, sometimes referred to as the method of cylindrical shells, is another technique commonly used to find the volume of a solid of revolution.
So, the idea is that we will revolve cylinders about the axis of revolution rather than rings or disks, as previously done using the disk or washer methods.
How does this work?
Geometrically, we know that the surface area of a cylinder is found by multiplying the circumference of the circular base times the height of the cylinder.
\begin{equation}
S A=2 \pi r h
\end{equation}
But this well known formula from geometry doesn’t take into account the thickness of the cylinder that is created.
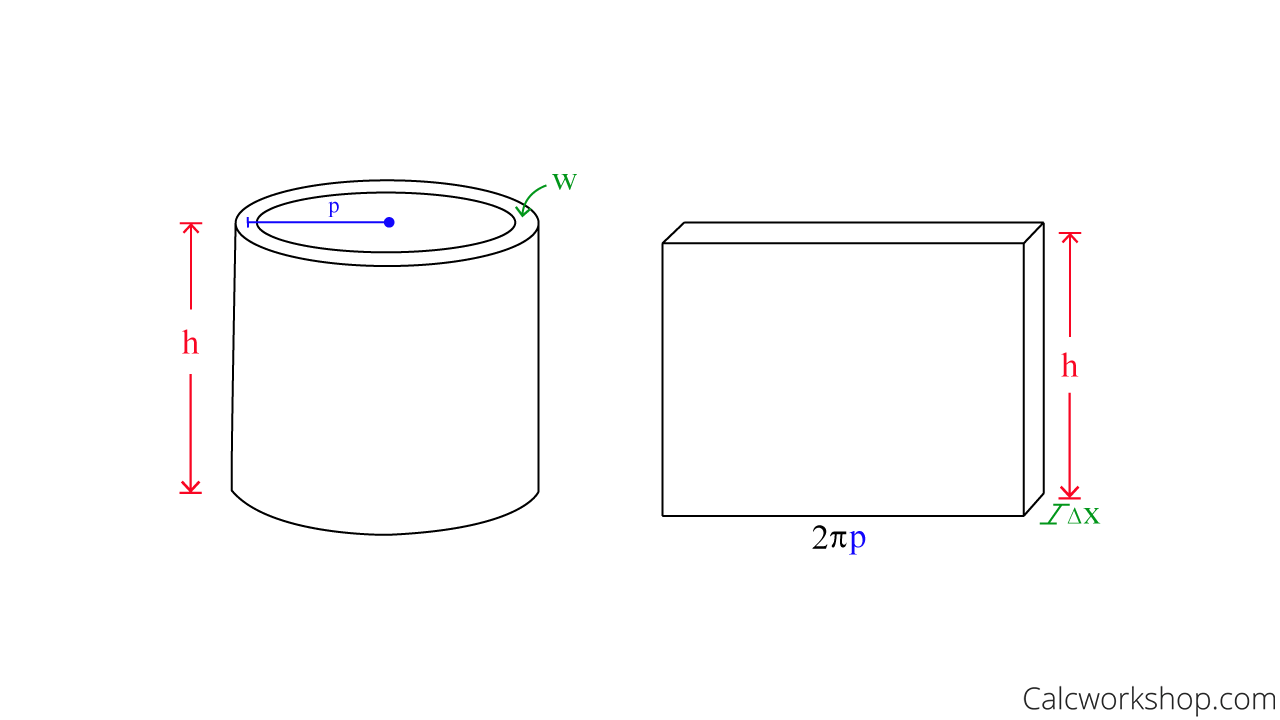
Surface Area Of Cylinder
\begin{equation}
S A=\underbrace{(\text { circumference })}_{2 \pi p} \underbrace{(\text { height })}_{h} \underbrace{(\text { thickness })}_{w}=2 \pi p h \Delta x
\end{equation}
And if we revolve an infinite number of cylinders, then the result is the volume of the solid. And we sum an infinite number of cylinders by
\begin{equation}
\lim _{n \rightarrow \infty} \sum_{i=1}^{n} 2 \pi(\text { radius })(\text { height })(\text { thickness })=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} 2 \pi p h \Delta x
\end{equation}
Disk Method Vs Shell Method
As the graphic below nicely illustrates, there is a considerable distinction between the disk method and the shell method.
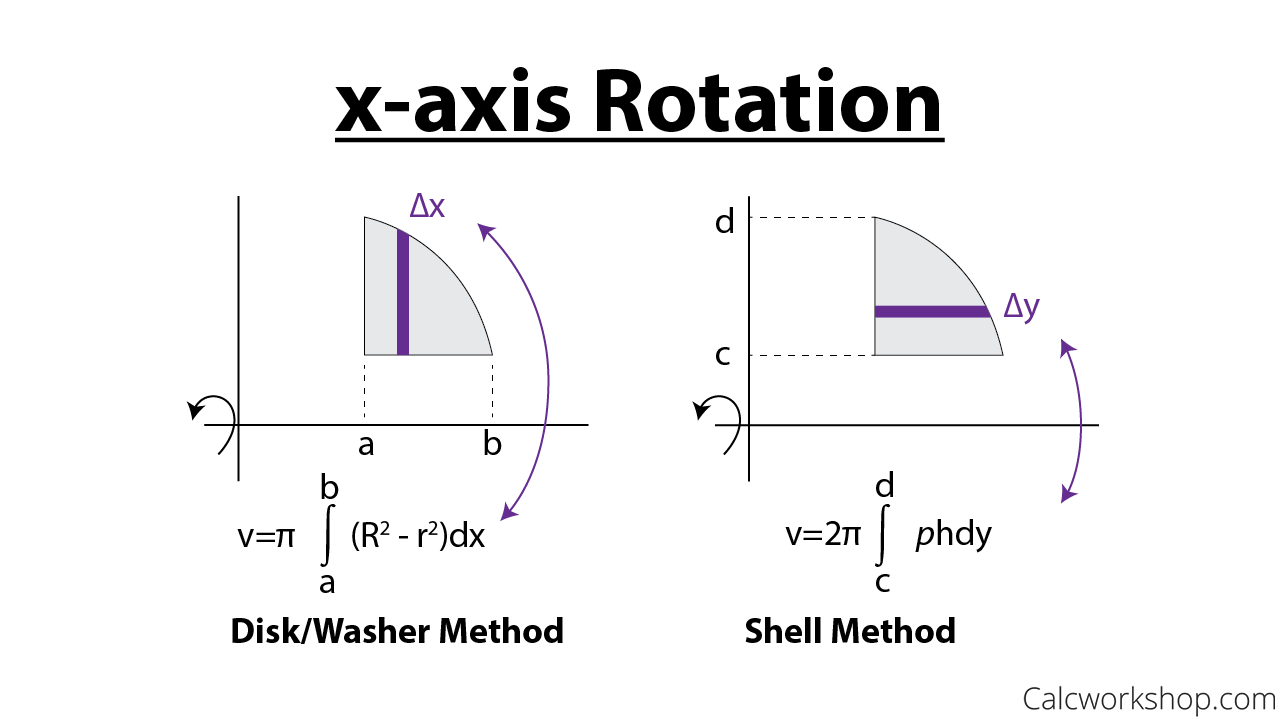
The Shell Method vs Disk Method (X-Axis)
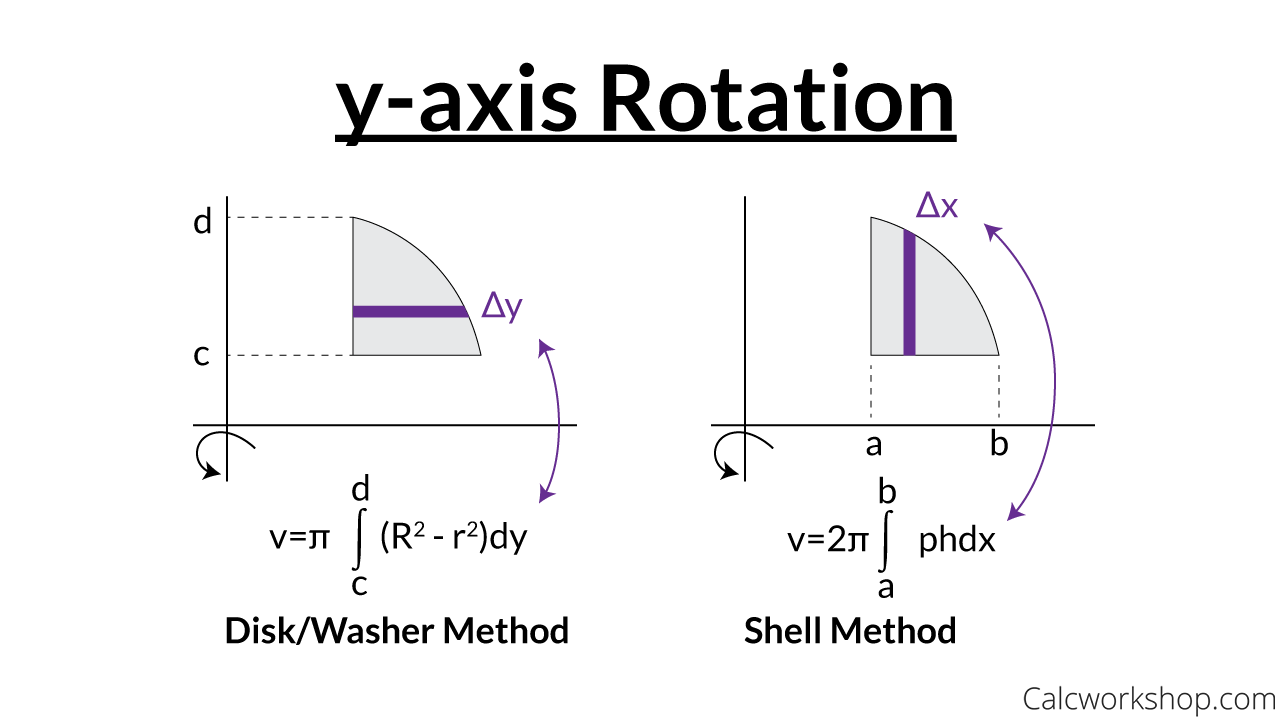
The Shell Method vs Disk Method (Y-Axis)
For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution.
Example
Okay, so let’s see the shell method in action to make sense of this new technique.
Find the volume of the solid obtained by rotating about the x-axis the region bounded between
\begin{equation}
y=x^{2}, y=0, x=0, \text { and } x=4
\end{equation}
First, let’s graph the region and find all points of intersection.
Find The Volume Of The Solid Generated By Revolving The Region Bounded
Now, let’s calculate the volume using the disk (washer) method and the shell method, side by side, and see how they compare.
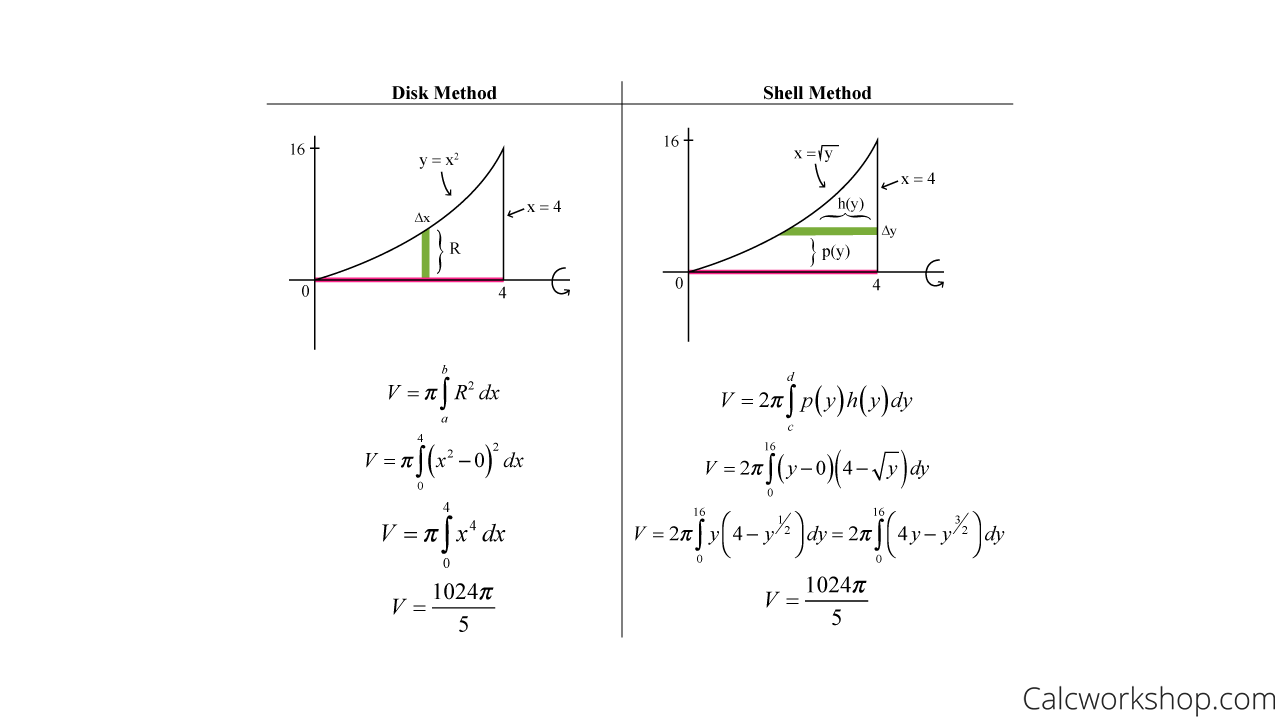
Disk Method Vs Shell Method
Isn’t it awesome to see that both methods yield the same result!
Cool!
But, if we can use either technique, how do you know when to use the shell or disk method?
So, as we saw with the example above, finding volume using the disk or washer method will produce the same result when calculating using the shell method. Consequently, the techniques are interchangeable, and it comes down to personal preference as to which integration technique you utilize. Yep, you get to choose which method you like better.
However, there are times when the shell method is the clear winner, as the disk method is insufficient.
Example
For instance, suppose we are asked to find the volume of the solid obtained by rotating about the y-axis the region bounded by
\begin{equation}
y=2 x^{2}-x^{3} \text { and } y=0
\end{equation}
First, let’s graph the region and find all points of intersection.
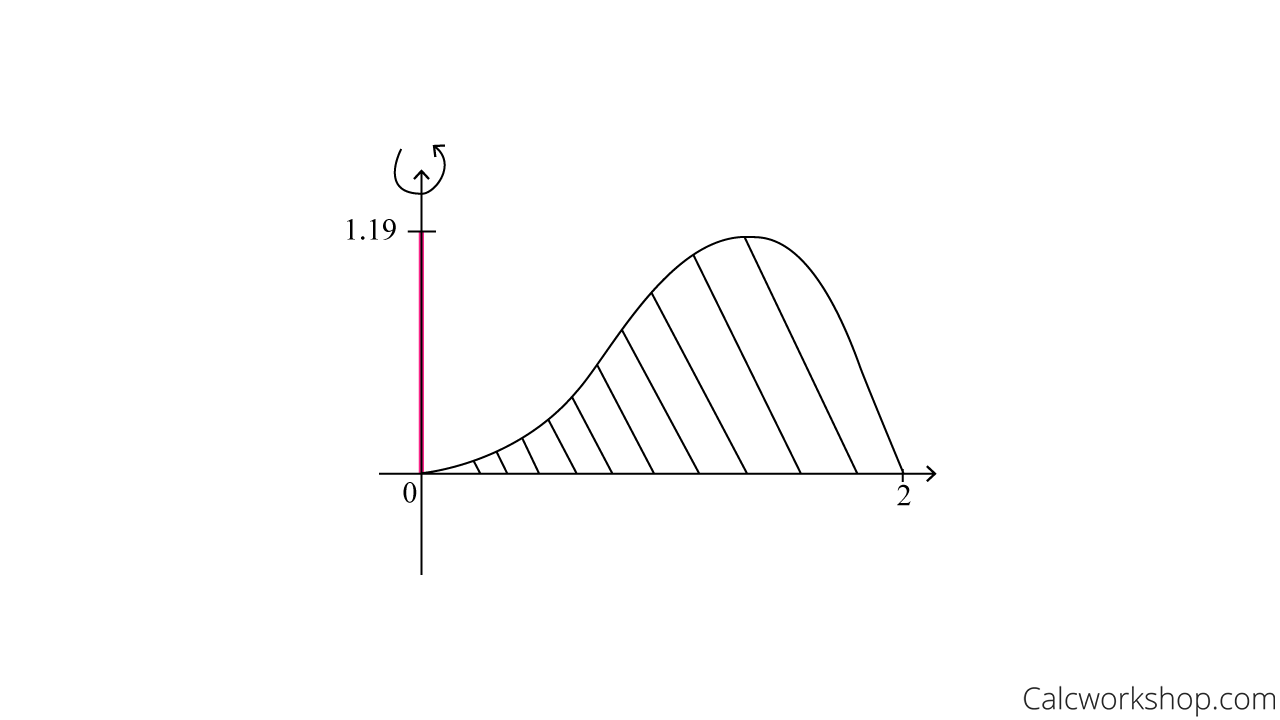
Shell Method Formula (Around Y-Axis)
And we quickly notice that if we tried to use the washer method, our “top” (outer) function is the same as the “bottom” (inner) function, which means they would eliminate each other!
Therefore, rather than using rectangles perpendicular to the axis of revolution, we must use rectangles parallel to the axis of rotation by using the shell method.
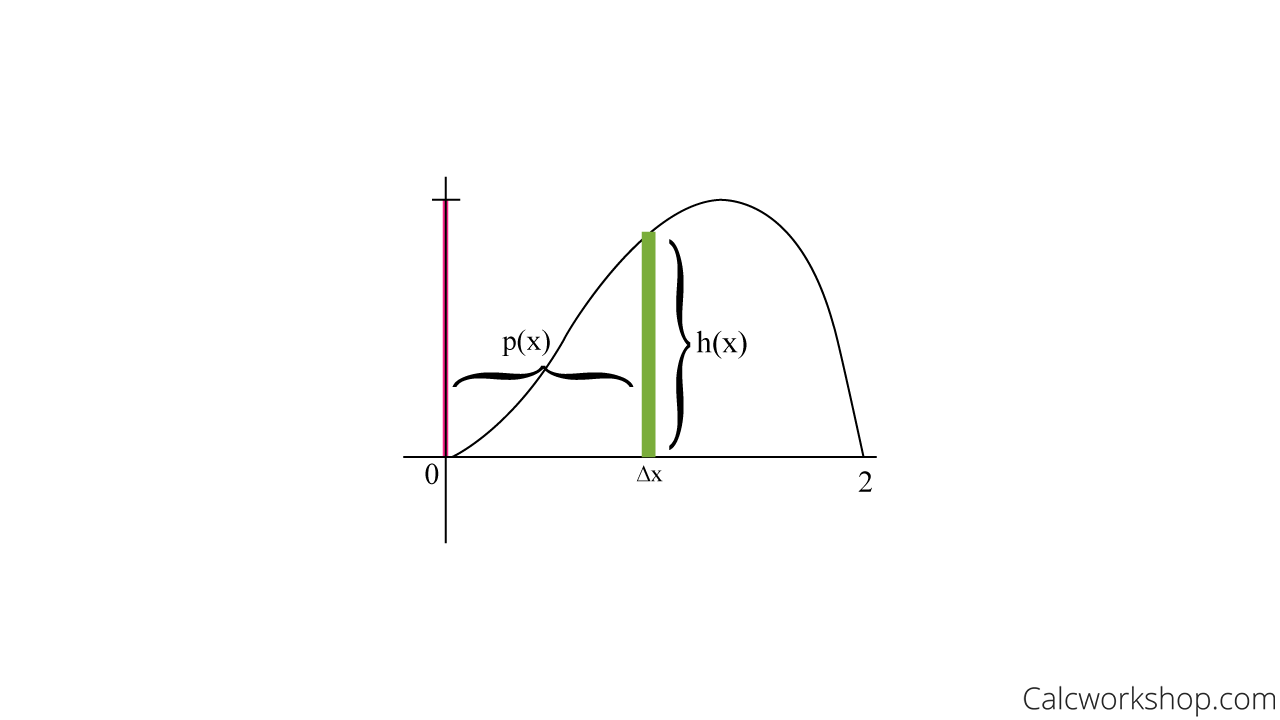
Shell Method (Finding Radius And Height)
\begin{equation}
\begin{array}{l}
V=2 \pi \int_{a}^{b} p(x) h(x) d x \\
V=2 \pi \int_{0}^{2}(x-0)\left(\left(2 x^{2}-x^{3}\right)-0\right) d x \\
V=2 \pi \int_{0}^{2} x\left(2 x^{2}-x^{3}\right) d x=2 \pi \int_{0}^{16}\left(2 x^{3}-x^{4}\right) d x \\
V=\frac{16 \pi}{5}
\end{array}
\end{equation}
Gosh, that means we were able to take a shaded region and revolve it about an axis to create a solid!
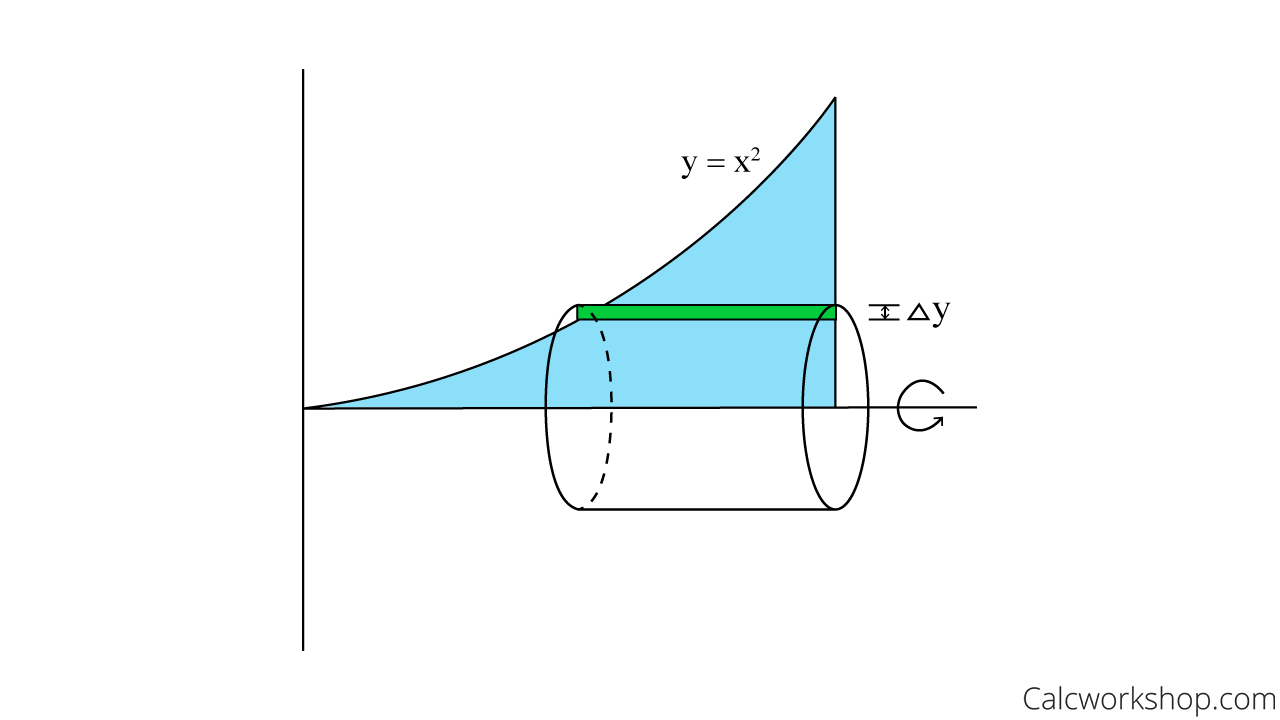
Volume Of Solid Of Revolution For Cylinder
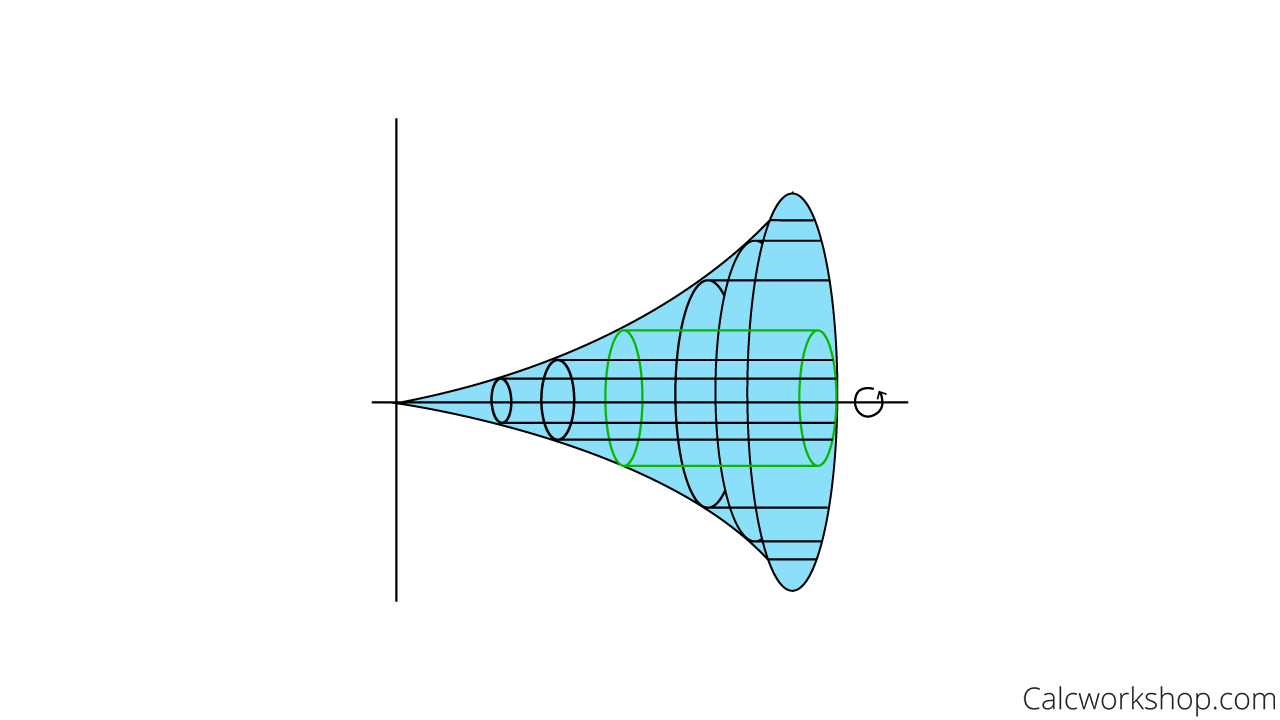
Approximation Of N Cylinders
See, this method is super handy and downright necessary!
Summary
Together, in this video lesson, we will walk through numerous examples in detail so that you will have a solid understanding of how and when to use this shell method to great success.
Let’s get after it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Solids of Revolution – Shell Method – 3 Examples
Shell Method Examples
- Overview of the Cylindrical Shell Method
- Example #1: Find the volume by rotating about the y-axis for the region bounded by y=2x^2-x^3 & y=0
- Example #2: Find the volume obtained by rotating about the y-axis for the region bounded by y=x & y=x^2
- Example #3: Find the volume obtained by rotating about the x-axis for the region bounded by y=x & y=x^2
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.