Imagine you are underwater in a pool. When you are just below the surface of the water, not too deep, you can feel a small amount of force on your head and face. As you go further down in the water, you can feel a lot more pressure.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
The sensation that you feel is hydrostatic force!
Hydrostatic force is a branch of fluid mechanics where we want to find the fluid force against an object, like:
- a river against a dam,
- an ocean against a ship’s hull,
- or even blood against your blood vessels.
Cool, right?
Types of Hydrostatic Force
Okay, so we will focus on three types of hydrostatic forces.
- Submerged Below Water Level
- Submerged at Water Level
- Partially Submerged
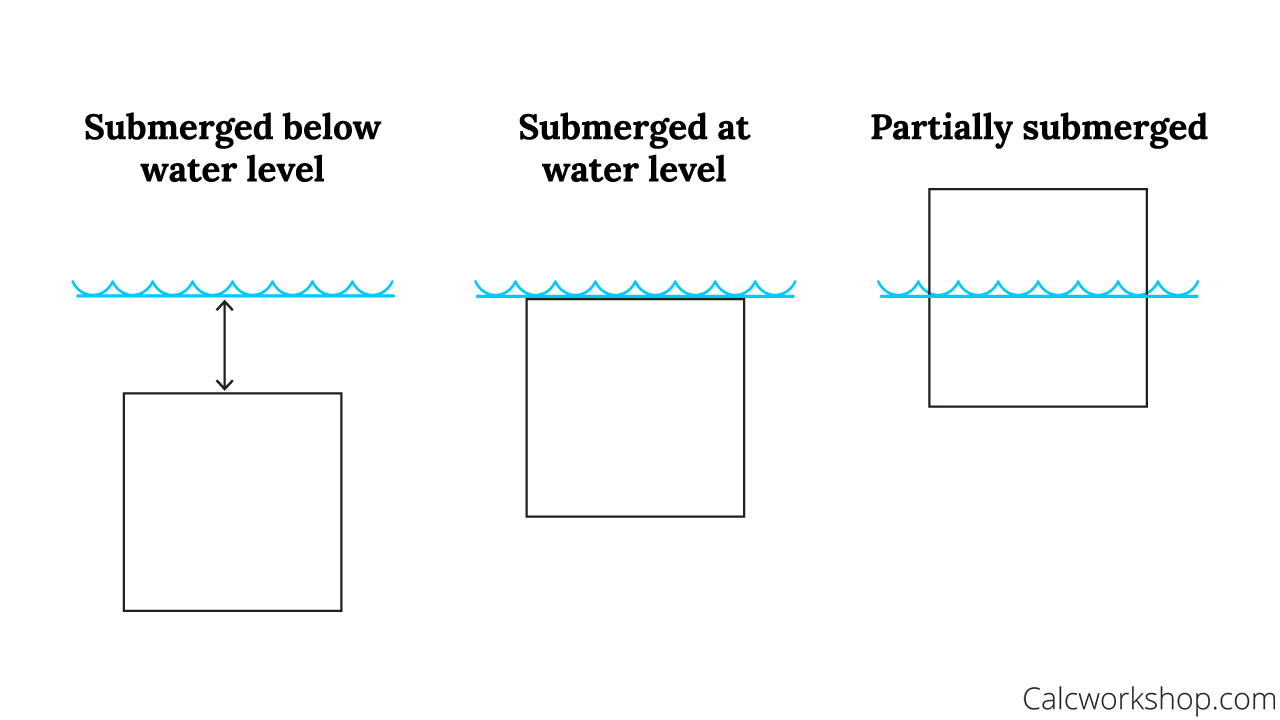
Three Types of Hydrostatic Forces
Understanding Pressure and Hydrostatic Pressure Equation
But before we can find fluid pressure and fluid force, we have to have a better understanding of pressure on an object.
Pressure is the force per unit of area on the surface of an object or body. And the deeper an object is submerged, the greater the pressure upon that object.
So, how do we define pressure?
The pressure on an object at a depth,
More specifically, the hydrostatic pressure equation describes the pressure at a certain depth within a fluid.
Where:
The equation is based on the assumption that the fluid is both incompressible and stationary, and it also takes into account that the pressure remains constant in the horizontal direction. In line with Pascal’s Principle, the pressure generated by a fluid at a particular depth is experienced uniformly in all directions, and can be calculated using the appropriate formula.
Weight-Density Constant – Don’t Make This Mistake
Now this formula seems super easy to use, right?
It is! But there is something sneaky going on that most students miss.
Pressure is found using a variable depth,
And it’s this weight-density constant that seems to cause unnecessary confusion. So, let’s make sense of it, so you won’t be fooled. The weight-density of a liquid is a constant (number) that behaves like a coefficient. We multiply this constant by the variable depth to find the fluid pressure,
Here is a list of some commonly used weight densities,
But sadly, the weight-density of water is still a heated debate, as scientists bicker over rounding. With that being said, depending on your textbook and the units of measure you are working in, you will see a slight variation in the weight-density constant that is used.
And if you are not told the liquid or units you are working with, then you will simply use a generic letter or symbol, like
For example,
Again, all this means is that we don’t need to multiply
All we have to do is grab the right weight-density constant from the tables above.
Calculating Force Exerted by a Fluid
Okay, so now we’re ready to use our knowledge to find the force exerted by a fluid on an object or body!
Integral Formula for Hydrostatic Force
Then the hydrostatic force acting on a vertical plate with a constant weight density is.
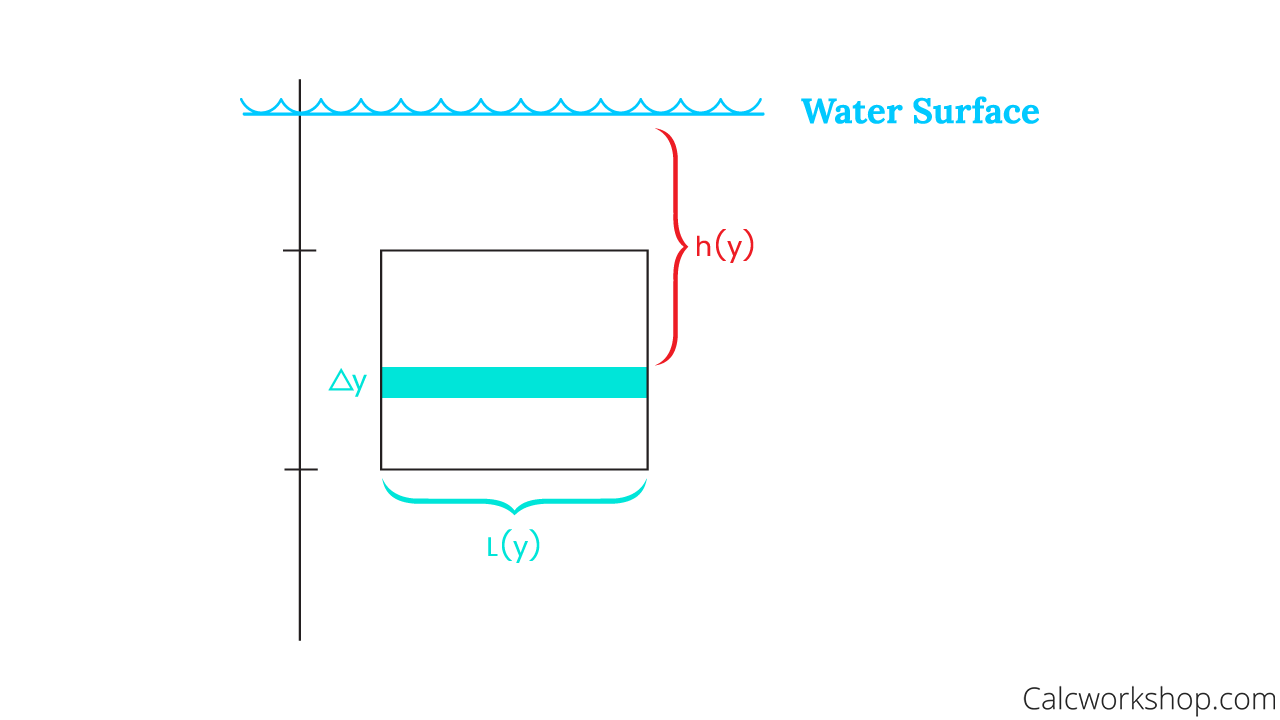
Calculating Hydrostatic Force
Now, this integral formula probably looks a bit overwhelming at first, but it’s not so bad once you know how to find all the pieces.
Let’s take a closer look by walking through an example together.
Example: Rectangular Plate
A rectangular plate that has a width of 3 meters and a height of 4 meters is submerged vertically in water so that the top of the plate is 5 meters below the water’s surface. Find the hydrostatic force against one side of the plate.

Rectangular Plate — Submerged Vertically
Step 1
First, we will redraw the vertical, rectangular plate so it is positioned on the
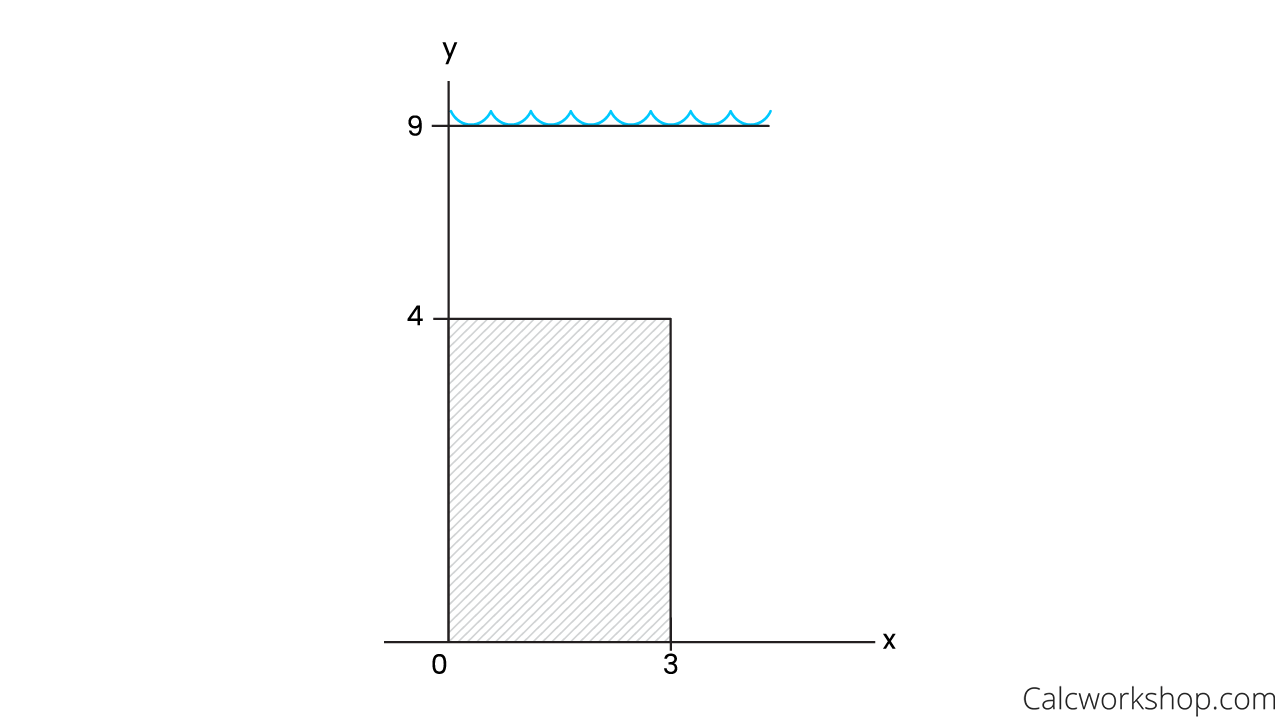
Rectangular Plate — XY Axes
Step 2
Second, we will place a horizontal strip in the rectangular plate with a width

Rectangular Plate — Delta Y Strip
Step 3
Third, we will determine our strip depth. Notice that the total water depth is 9 meters, so the depth from the water level to our horizontal strip is

Calculating Hydrostatic Force
Step 4
Next, we will calculate the strip length, length
Now we are ready to find our limits of integration, or our “c” and “d” values, and our weight density constant. What is important to note is that these values measure the height of the rectangular plate only. Thus, our submerged plane is from
Step 5
Lastly, we drop all our expressions into our handy-dandy formula, simplify, and integrate!
This means the force acting on this rectangular plate is
Next Steps
While tackling hydrostatic force problems, it’s essential to:
- Draw and label diagrams: This will assist you in visualizing the problem and organizing the necessary information.
- Recognize symmetry: Identifying symmetry in your problems can simplify calculations and help you find solutions more efficiently.
Together, we’ll explore numerous examples with various shapes, such as:
- Squares, rectangles, triangles, trapezoids, and semicircles
During the process, I’ll help you recall essential algebra, geometry, and trigonometry rules while we calculate fluid force.
Though it may seem overwhelming initially, I assure you that this video will keep you afloat and guide you through hydrostatic force problems with ease. Join me as we investigate hydrostatic force together!
Video Tutorial w/ Full Lesson & Detailed Examples

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.