Particle Motion In Calculus
w/ 5 Step-by-Step Examples!

Did you know that motion is relative?

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

It’s true!

For instance…

By stating that a vehicle is moving at 60 miles per hour, we are really referring to the rate of motion in relation to the surface the vehicle is traveling on.

Thus, the speed of an airplane is its motion in relation to the air and that of a ship is its motion in relation to the water.

Let’s dig deeper…

Particle Motion Defined

In light of the fact that particle motion requires a frame of reference, we will utilize the coordinate axes and four key ideas:

• Position
• Velocity
• Acceleration
• Speed

Position determines where a particle or object is located on the x-axis at a given time and is denoted by s(t) or x(t).

Velocity determines how fast the position is changing at time t and gives the direction of movement. Velocity is denoted as v(t) = s’(t)

Acceleration determines how fast the velocity is changing at time t and shows if the velocity increases or decreases. Acceleration is denoted by a(t) = v’(t) = s’’(t)

Velocity is a vector that has magnitude and direction, but speed is a scalar (number) that expresses the absolute speed of an object. Speed indicates how fast an object is moving, but velocity represents speed in a given direction.

Therefore, if s(t) represents the position of a particle along the x-axis at any time t, then the following terms are of importance to our understanding of motion.

• “initially” means when time t=0
• “at the origin” means when the position s(t) = 0
• “at rest” means the velocity v(t) = 0

Step-by-Step Example

Having laid the foundation, let’s move on to learn about particle motion through an example and review some previously learned skills and terms.

Suppose we are given the following position function, measured in meters, \(s(t)=2 t^{3}-2 t^{2}+4\)

Initial Position

What is the object’s initial position?

\begin{equation}
s(0)=2(0)^{3}-2(0)^{2}+4=4
\end{equation}

So, when t = 0, the position of the particle is 4 meters.

Velocity

Now let’s determine the velocity of the particle by taking the first derivative.

\begin{equation}
v(t)=s^{\prime}(t)=6 t^{2}-4 t
\end{equation}

Next, let’s find out when the particle is at rest by taking the velocity function and setting it equal to zero.

\begin{equation}
\begin{array}{l}
v(t)=0 \\
6 t^{2}-4 t=0 \\
2 t(3 t-2)=0 \\
t=0, \frac{2}{3}
\end{array}
\end{equation}

Based on our calculations, we find that the particle is at rest at time t = 0 and t = 2/3.

But now, for the interesting question.

During what intervals does the particle move left and right?

Decoding this requires us to search for increasing and decreasing intervals.

Why?

Because when the velocity is positive, the particle moves toward the right, and when the velocity is negative, the particle moves toward the left.

Ahh, so we were actually finding critical numbers when we found v(t) = 0. If we test for either positive or negative values on either side of our critical numbers, we will be able to determine when the particle is moving right or left!

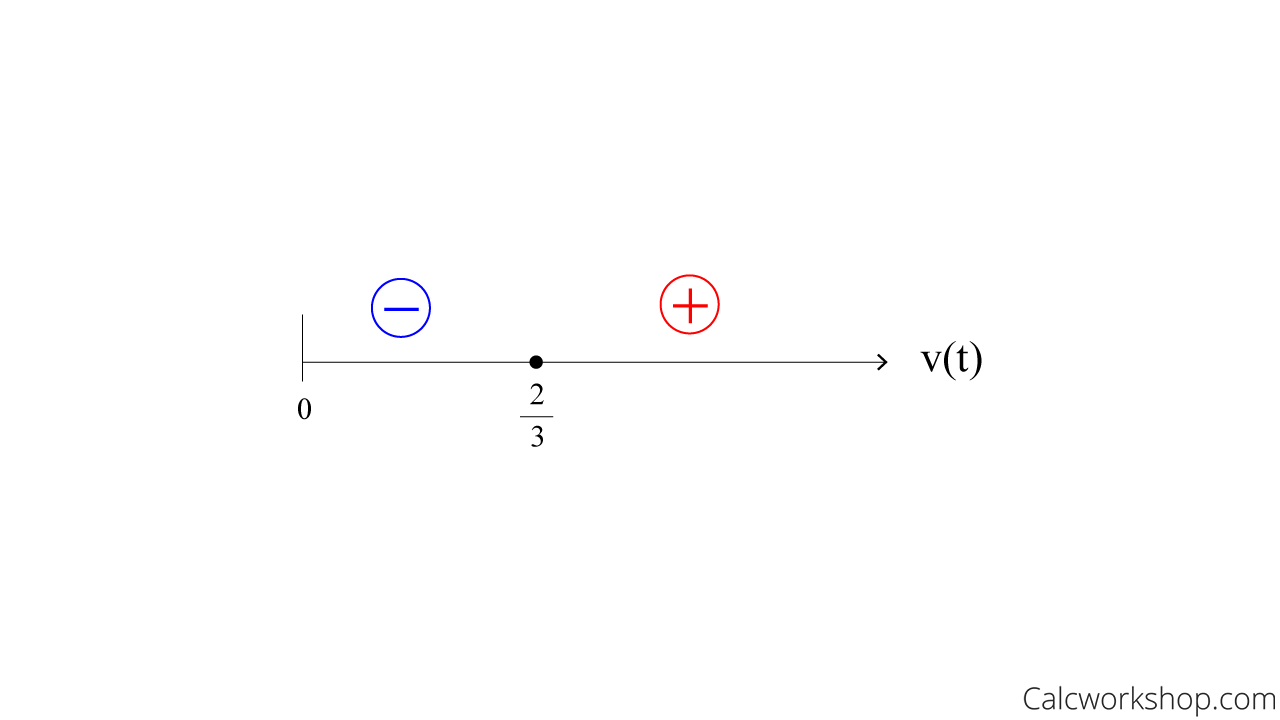
Velocity Number Line

\begin{equation}
\begin{array}{l}
\text { Moving Right: } t \in\left(\frac{2}{3}, \infty\right), v(t)>0 \\
\text { Moving Left: } t \in\left(0, \frac{2}{3}\right), v(t)<0 \end{array} \end{equation} Clearly, this raises the question of whether the particle changes direction? And if so, at what point? Okay, so I want you to imagine a ball being thrown into the air. When it reaches its apex (maximum height), it turns back around and falls to the ground, right?

This means that the particle will turn around at any extreme value, such as a relative maximum or relative minimum.

So, all we have to do is find our local extrema to determine if the particle changes direction!

Again, using our number line, we can see that at t = 2/3, the particle changes from moving left (negative velocity) to moving right (positive velocity). Therefore, the particle changes direction at t = 2/3.

Acceleration

Alright, now it’s time to find the acceleration of the particle. We do this by taking the second derivative of the position function, which is nothing more than the derivative of the velocity.

\begin{equation}
a(t)=v^{\prime}(t)=s^{\prime \prime}(t)=12 t-4
\end{equation}

Okay, so now let’s determine the intervals for where the velocity is increasing or decreasing.

First, we must find when the acceleration is at rest, so we set the acceleration function equal to zero.

\begin{equation}
\begin{array}{l}
a(t)=0 \\
12 t-4=0 \\
t=\frac{4}{12}=\frac{1}{3}
\end{array}
\end{equation}

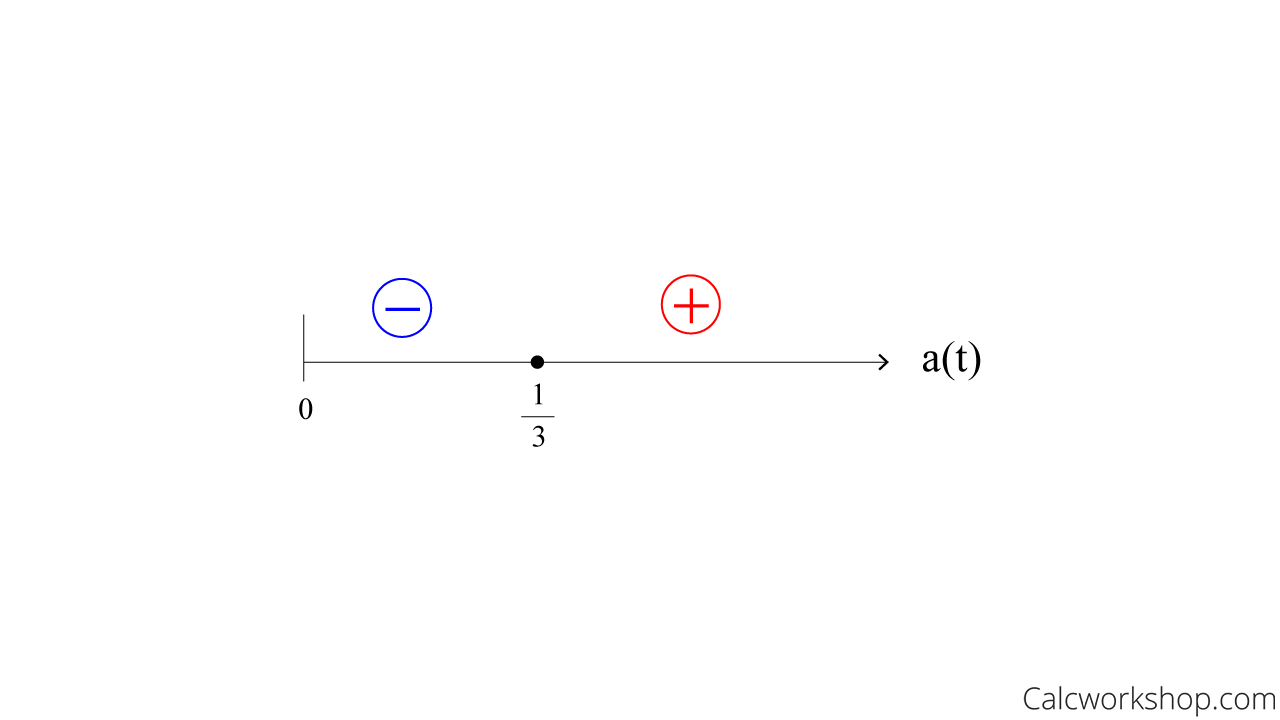
Acceleration Number Line

This means that the velocity is increasing (concave up) to the right of 1/3, and the velocity is decreasing (concave down) from 0 to 1/3.

Speed

Now it’s time to look at speed!

Despite the fact that particle speed is the absolute value of its velocity, this doesn’t really tell us much about how the particle behaves. What we want to know is when the particle’s speed is increasing or decreasing.

And here’s an important fact:

Whenever the particle’s velocity and acceleration have the same sign (positive or negative), the particle’s speed is increasing. Likewise, when the particle’s velocity and acceleration have opposing signs (one positive, one negative), the particle’s speed is decreasing.

And the best way to determine this is to compare our two number lines!

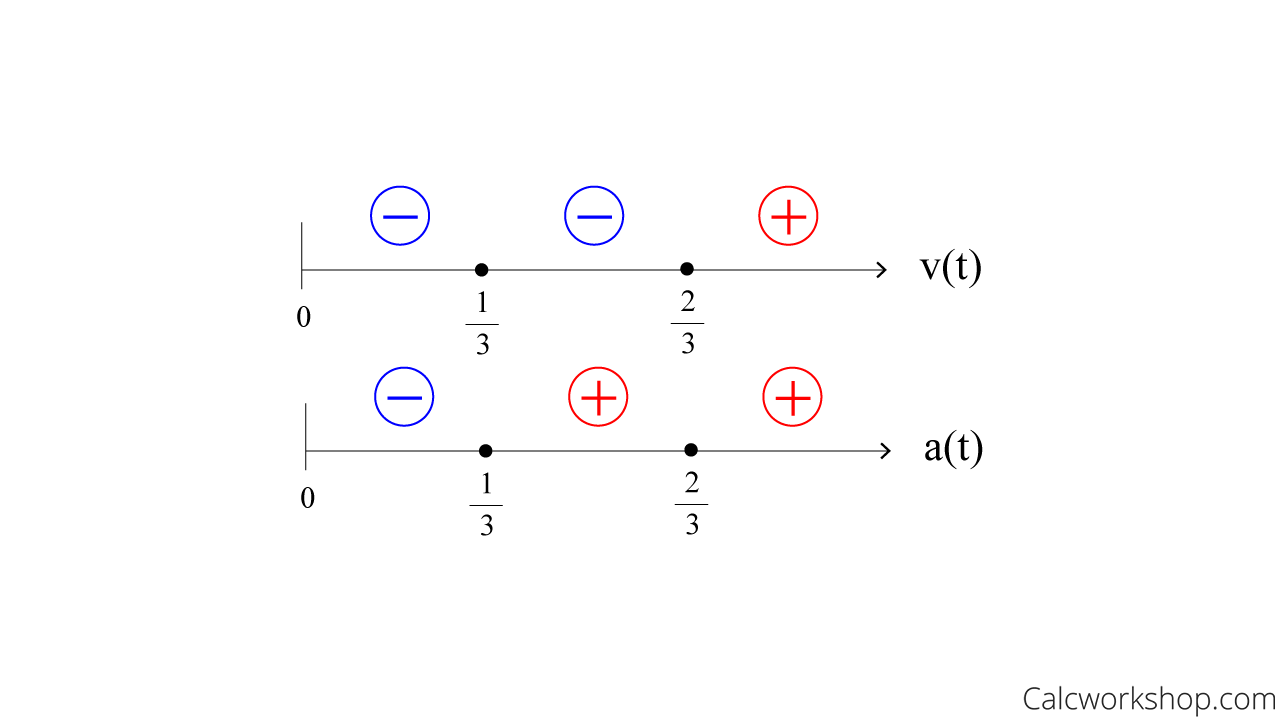
Find Speed Using Velocity Acceleration

\begin{equation}
\begin{array}{l}
\text { Speed Increasing: } t \in\left(0, \frac{1}{3}\right) \cup\left(\frac{2}{3}, \infty\right) \\
\text { Speed Decreasing: } t \in\left(\frac{1}{3}, \frac{2}{3}\right)
\end{array}
\end{equation}

Distance Vs Displacement

Now it’s time to look at distance and displacement.

What’s the difference?

Distance or “total distance” measures the length of a particle or object’s path taken over a period of time. Displacement measures how far the particle or object traveled, regardless of whether it doubled back or turned around.

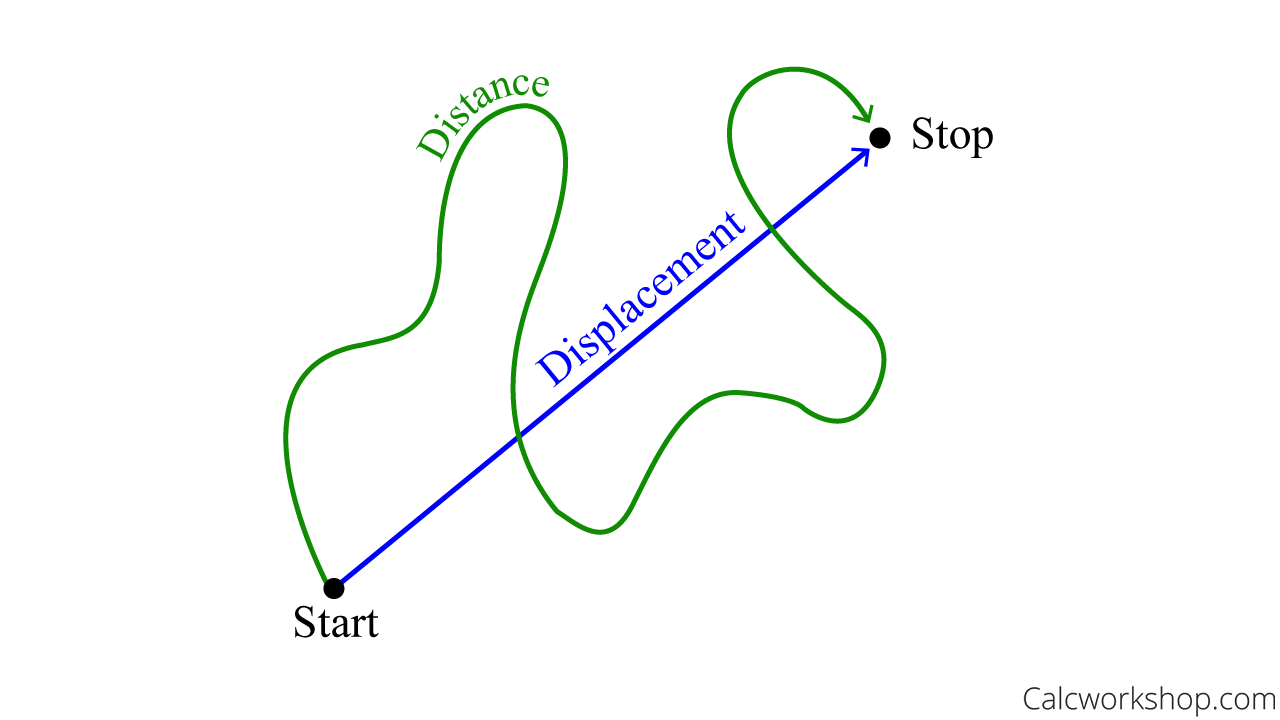
Distance Vs Displacement

The Equations

To calculate the displacement, just substitute the ending and starting times into the position function and subtract.

\begin{equation}
s(\text { stop })-s(\text { start })=s(b)-s(a)
\end{equation}

To calculate the distance, we must calculate the absolute value of the difference in position between all resting points.

\begin{equation}
\mid s(\text { stop })-s(\text { start })|=| s(b)-s(a) \mid
\end{equation}

Worked Example

So, going back to our original example where \(s(t)=2 t^{3}-2 t^{2}+4\) let’s first find the displacement of the particle from \(0 \leq t \leq 5\).

\begin{equation}
s(5)-s(0)=\left[2(5)^{3}-2(5)^{2}+4\right]-\left[2(0)^{3}-2(0)^{2}+4\right]=204-4=200
\end{equation}

So, the displacement of the particle is 200 meters.

Now let’s find the distance traveled by the particle from \(0 \leq t \leq 5\) knowing that our particle rested at \(t=\frac{2}{3}\) from our previous analysis of the velocity.

Thus, we can calculate the distance as follows:

\begin{equation}
\begin{array}{l}
|s(5)-s(0)|=\mid s(\text { rest })-s(\text { start })|+| s(\text { stop })-s(\text { rest })|=| s\left(\frac{2}{3}\right)-s(0)|+| s(5)-s\left(\frac{2}{3}\right) \mid \\
\left|\left(2\left(\frac{2}{3}\right)^{3}-2\left(\frac{2}{3}\right)^{2}+4\right)-\left(2(0)^{3}-2(0)^{2}+4\right)\right|+\left(2(5)^{3}-2(5)^{2}+4\right)-\left(2\left(\frac{2}{3}\right)^{3}-2\left(\frac{2}{3}\right)^{2}+4\right) \mid \\
\left|\frac{100}{7}-4\right|+\left|204-\frac{100}{7}\right|=\frac{8}{27}+\frac{5408}{27}=\frac{5416}{27} \approx 200.593
\end{array}
\end{equation}

Taking into account the brief period of time the particle moved to the left, rested, turned, and traveled to the right, it traveled a total of 200.593 meters.

We can learn so much from one little function, right?

Together in this video lesson, we will explore particle motion, find when an object is moving right or left, at rest, increasing velocity and speed, and distance and average rates of change.

Here we go, it’s gonna be fun!

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.