So what is the first derivative test?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In a nutshell, the first derivative test enables us to find increasing and decreasing intervals, critical numbers, and relative extrema.
Let’s dive in and see how this works!
Backstory
The concept of increasing and decreasing is not new to us.
Looking at the weather app on your phone tells us the increase and decrease of daily temperatures. Business analysts calculate the percentage of increase or decrease in sales of stocks. And we use fitness trackers to help us know when to increase our daily step count to decrease our chance of heart disease.
In calculus, the first derivative test allows us to quickly find those intervals of increase and decrease for a function as well identifying maximum and minimums values. In doing so, we become just like those apps we install on our phone – knowing when the weather will be balmy, sell a stock, or walk a few more steps.
Increasing And Decreasing Functions
Okay, so how do we define increasing and decreasing functions?
A function is increasing on an interval if for any two numbers c and d in the interval, if c < d then f(c) < f(d). And a function is decreasing on an interval if for any two numbers c and d in the interval, if c < d then f(c) > f(d).
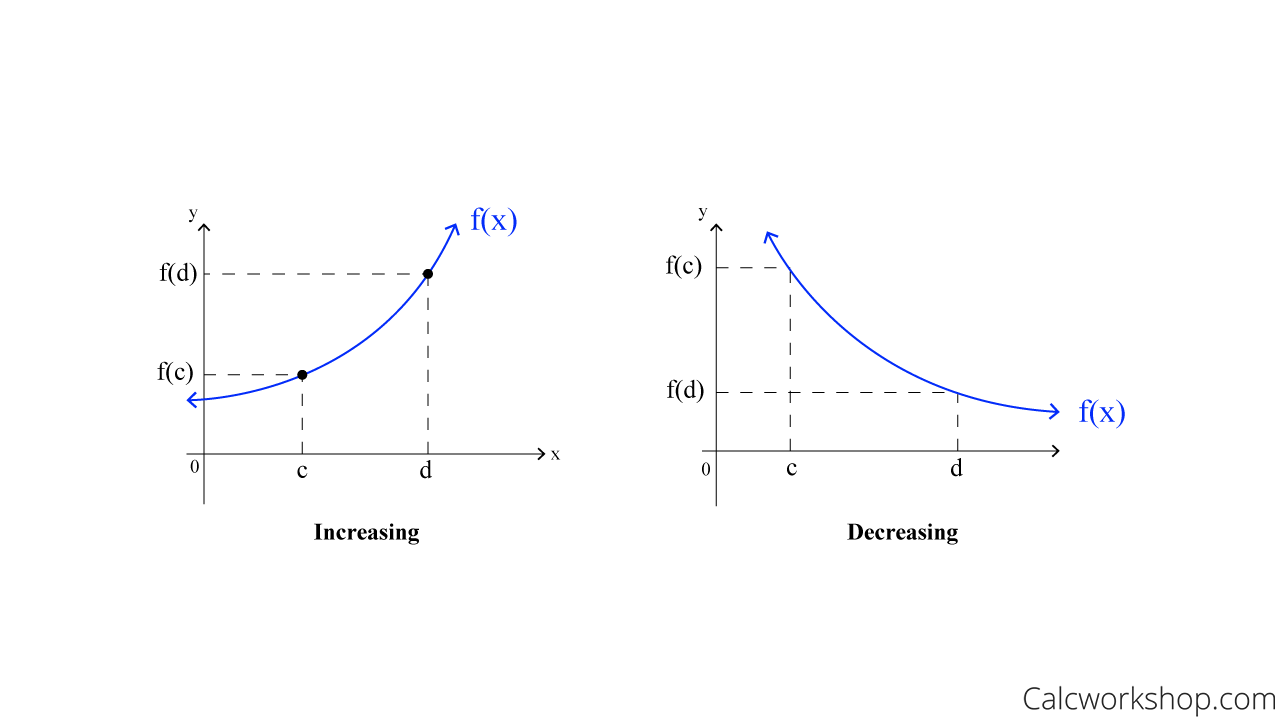
Increasing And Decreasing Functions
In other words, increasing means the function is moving upward, and decreasing implies the function is moving downward.
Increasing And Decreasing Intervals
But how do you find increasing and decreasing intervals?
By looking at the slope of the curve.
If the slope (i.e., first derivative) is positive, then the function increases, whereas if the slope is negative, then the function decreases!
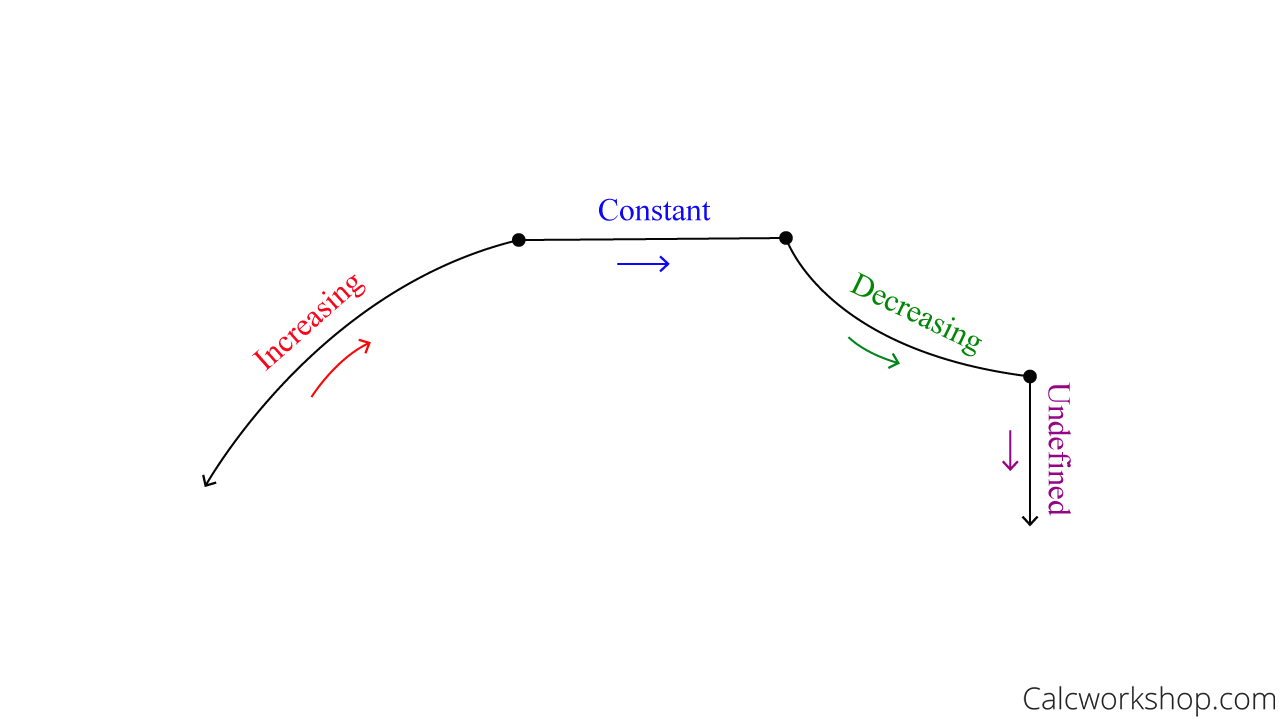
Slope Increasing Constant Decreasing Undefined
In summary:
- If f’ (x) > 0 for all x in the interval, the function f is increasing.
- If f’(x) < 0 for all x in the interval, then function f is decreasing.
- If f’ (x)=0 for all x in the interval, then function f is constant.
Example – Define Intervals
For example, suppose we want to find all the increasing and decreasing intervals for the function:
\begin{equation}
f(x)=3 x^{2}-12 x+1
\end{equation}
First, we will find our critical numbers by using the power rule to find the first derivative and set it equal to zero and solve.
\begin{equation}
\begin{array}{l}
f^{\prime}(x)=6 x-12 \\
6 x-12=0 \\
x=2
\end{array}
\end{equation}
Next, we will test numbers on either side of 2 to determine whether the value is positive or negative.
Let’s use x = 1 and x = 3 as our test points.
\begin{equation}
\begin{array}{l}
f^{\prime}(1)=6(1)-12=-6, \quad f^{\prime}(1)<0 \\
f^{\prime}(3)=6(3)-12=6, \quad f^{\prime}(3)>0
\end{array}
\end{equation}
This means that our function decreases to the left of x = 2 and increases to the right of x = 2.
Increasing Interval: \(x \in(2, \infty)\)
Decreasing Interval: \(x \in(-\infty, 2)\)
Pretty easy, right?
Now here’s what’s unique about all of this. As you know, a function can change from increasing to decreasing, and it’s at these critical points where extrema exist.
First Derivative Test – Defined
The First Derivative Test states that if we are given a continuous and differentiable function f, and c is a critical number of function f, then f(c) can be classified as follows:
- If f’ (x) changes from negative to positive at c, then f(c) is a relative minimum.
- If f’ (x) changes from positive to negative at c, then f(c) is a relative maximum.
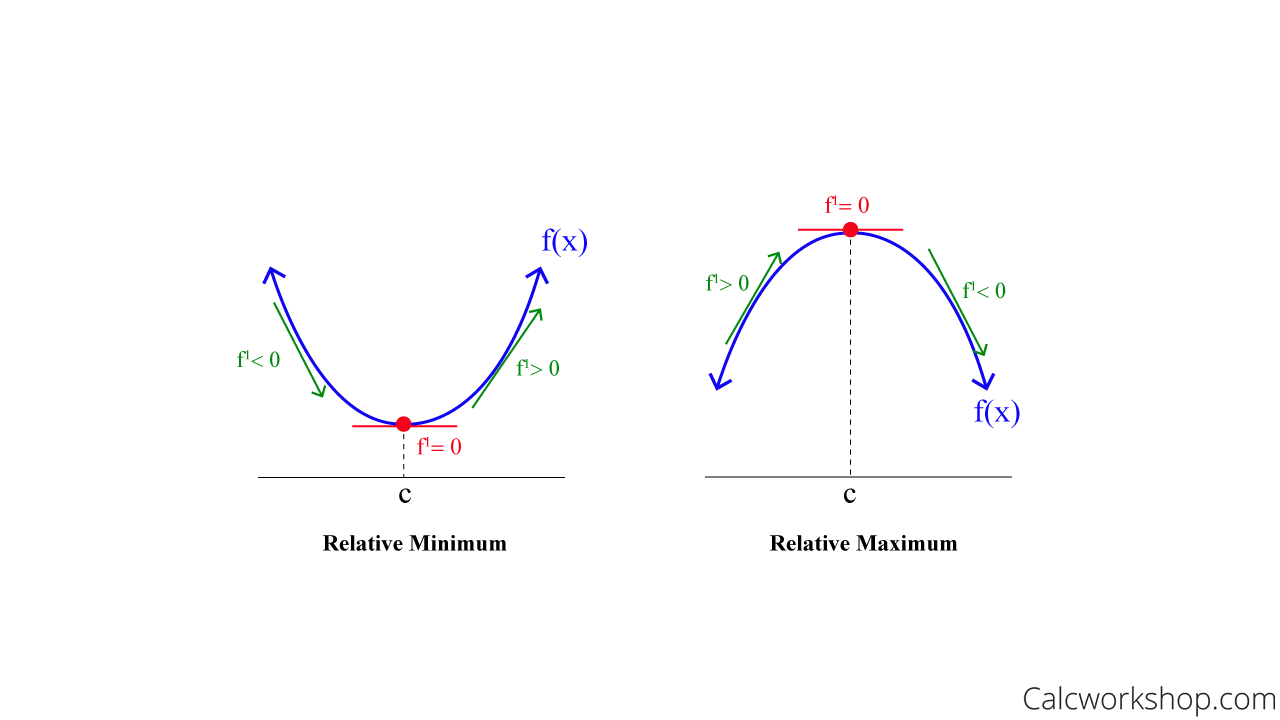
Relative Maximum And Minimum
Example – Relative Extrema
Suppose we want to find all increasing and decreasing intervals and all relative extrema for the function:
\begin{equation}
f(x)=\frac{1}{3} x^{3}-\frac{1}{2} x^{2}-6 x
\end{equation}
First, we will find our critical numbers by setting our first derivative equal to zero and solving.
\begin{equation}
\begin{array}{l}
f^{\prime}(x)=x^{2}-x-6 \\
x^{2}-x-6=0 \\
(x-3)(x+2)=0 \\
x=-2,3
\end{array}
\end{equation}
Next, we will test points on either side of our critical numbers to determine whether the value is positive or negative.
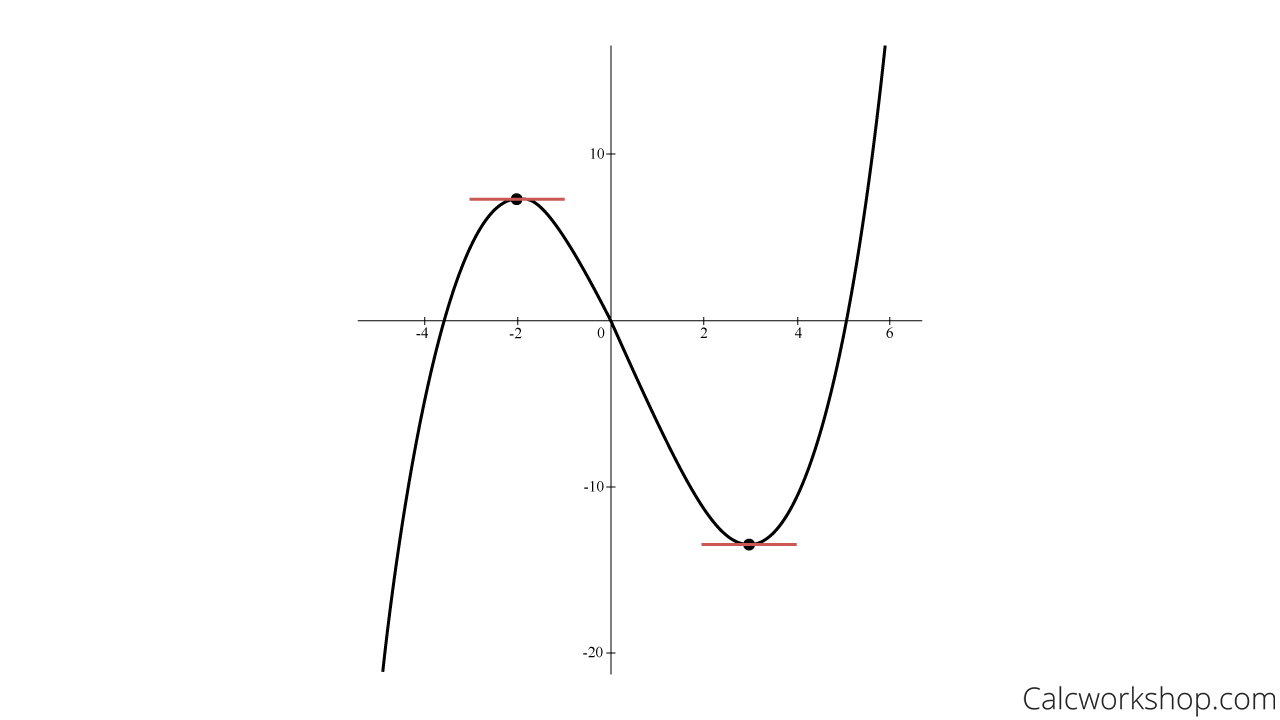
This means that our function is increasing to the left of x = -2 and to the right of x = 3, and the function is decreasing between x = -2 and x = 3.
Increasing Interval: \(x \in(-\infty,-2) \cup(3, \infty)\)
Decreasing Interval: \(x \in(-2,3)\)
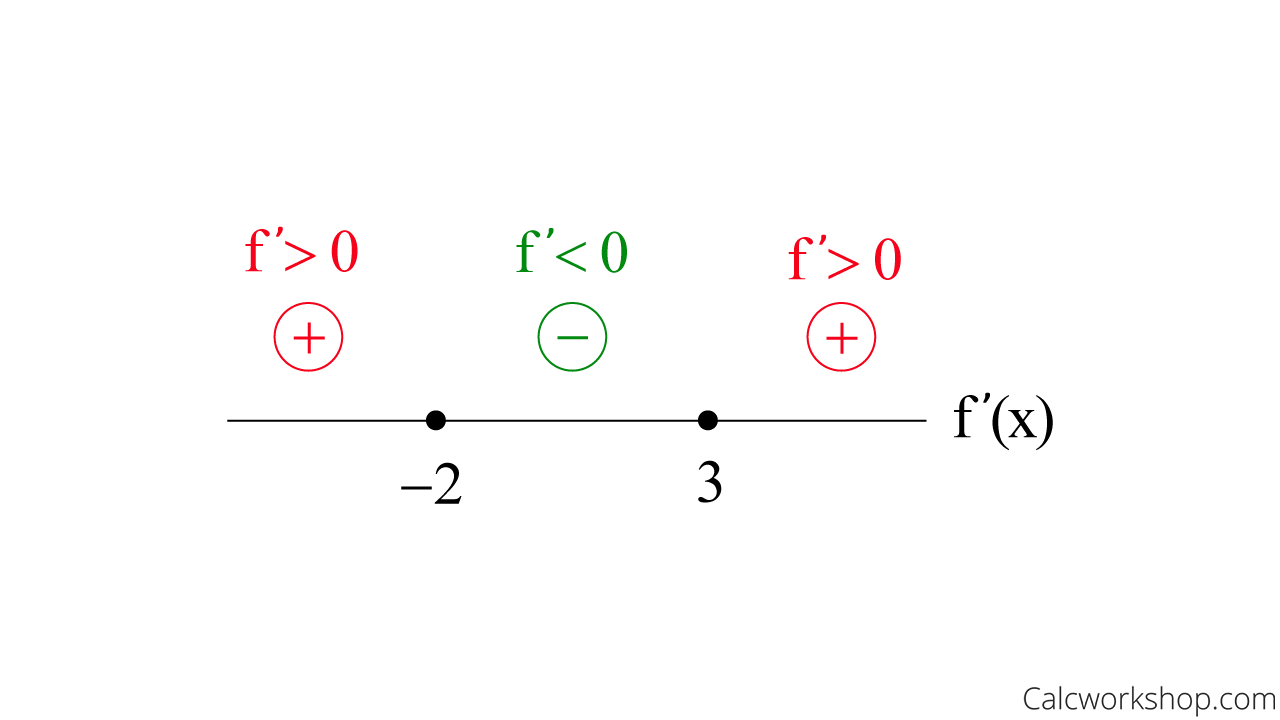
First Derivative Number Line
Furthermore, at x = 3, the slope changes from negative to positive. This means that the functions changes from decreasing to increasing, so we know that x = 3 must be a relative minimum.
Identify Relative Max Min Example
Cool!
So, what have we discovered?
If the function changes from increasing to decreasing, we have a maximum, and if it changes from decreasing to increasing, we have a minimum! Sweet!
Example – No Relative Extremum
But what happens if the function doesn’t change from positive slope to negative slope or vice versa?
When this happens, we do not have a relative extremum, as seen by the following example.
Suppose we want to find all increasing and decreasing intervals and all relative extrema for the function:
\begin{equation}
f(x)=x^{3}
\end{equation}
First, we will find our critical numbers by setting our first derivative equal to zero and solving.
\begin{equation}
\begin{array}{l}
f^{\prime}(x)=3 x^{2} \\
3 x^{2}=0 \\
x=0
\end{array}
\end{equation}
Next, we will test points on either side of our critical numbers to determine whether the value is positive or negative. Let’s use x = -1 and x = 1 as our test points
\begin{equation}
\begin{array}{l}
f^{\prime}(-1)=3(-1)^{2}=3, f^{\prime}(-1)>0 \\
f^{\prime}(1)=3(1)^{2}=3, f^{\prime}(1)>0
\end{array}
\end{equation}
In other words, our function is strictly increasing, or a monotonic increasing function, because the slope of the curve is entirely positive.
Increasing Interval: \(x \in(-\infty, 0) \cup(0, \infty)\)
Decreasing Interval: n/a

Find Critical Number First Derivative Test
Consequently, there are no relative extrema because our function never changes from increasing to decreasing or decreasing to increasing.
But don’t worry, just because we didn’t find a local minimum or local max doesn’t mean that this type of function doesn’t have special properties. In fact, in our next lesson, we’re going to learn all about inflection points, concavity, and shape – exciting!
Together, we will use the first derivative test to find increasing and decreasing intervals and determine if our critical numbers yield relative extrema.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.