How do you find absolute extrema?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Great question!
And that’s exactly what you’re going to learn in today’s calculus class.
Let’s go!
Big Idea
If you’ve ever ridden inside an elevator, frequented a movie theater, or lounged the day away at a public pool, then you’ve probably noticed a sign saying, “maximum capacity.”
Gosh, even our smartphones have a limit on battery and storage capacity.
But have you ever stopped to wonder what does this really means?
Well, “maximum” is an extreme value, which tells us the biggest value that can be taken on. Therefore, maximum capacity is the largest value deemed safe or acceptable for a certain space to hold or allow.
But how do you determine these extreme values (i.e., optimal outcomes)?
Well, many important applications in calculus deal with optimization, like maximizing profit and minimizing cost, and all we have to do is use the derivative to find our extrema.
Some Definitions For Clarity
Extrema are the maximum or minimum values of a function, and there are two types of extrema we will be focusing on:
- Absolute (global) Extrema
- Local (relative) Extrema
Absolute extrema represents the highest and lowest points on a curve, whereas the term local extrema refers to any high and low point within the interval.
So, using the graph of function f below for the interval [a,e], we can visually see that the highest point (absolute maximum) is when x = e and the lowest point (absolute minimum) is when x = d.
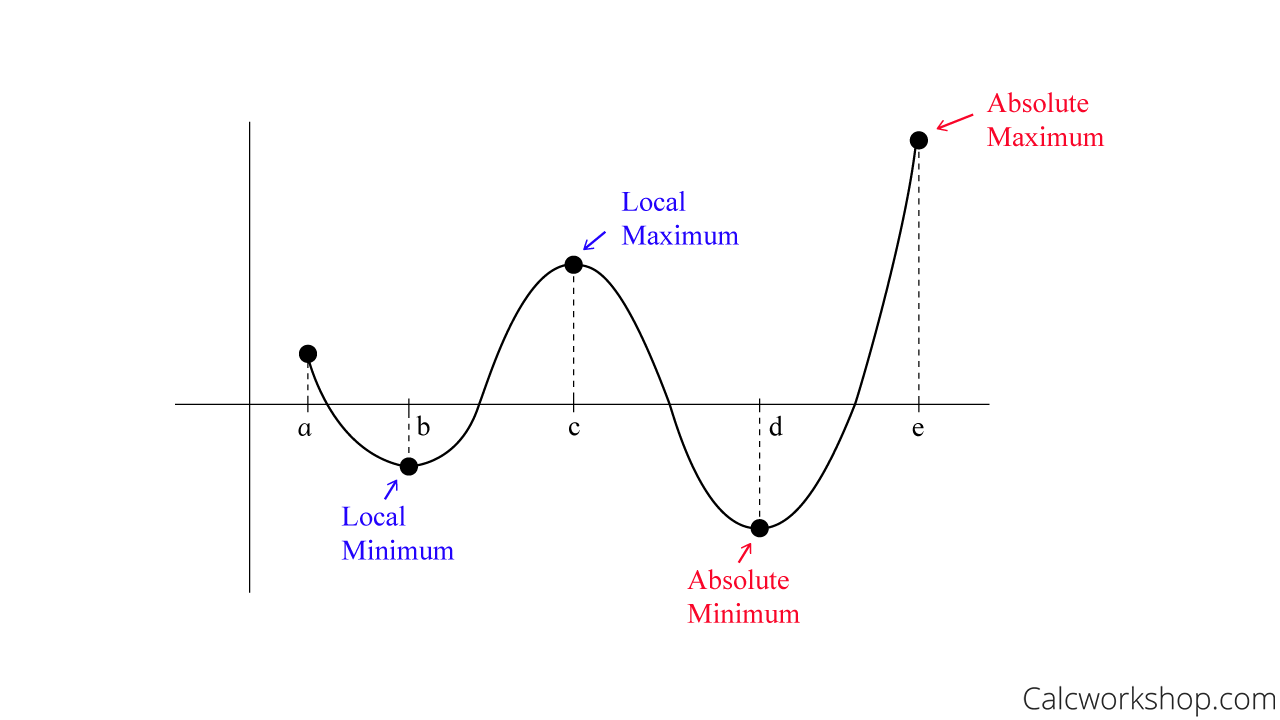
Local Vs Absolute Extrema
But we also observe that there are other “high” and “low” points within the interval. These are considered local (relative) extrema.
It’s important to point out that Absolute Extrema can occur within the interval or at the endpoints. In contrast, Local Extrema can only be found within the open interval and never at an endpoint.
Okay, but this now leads us to another important question.
Are you always guaranteed to have an extreme value?
The Extreme Value Theorem states that if f is a continuous function on a closed interval [a,b], then f will have an absolute minimum f(c) and an absolute maximum f(d) at some values c and d in the interval.
Minimum Vs Maximum
The Role Of “Critical Numbers”
But without a graph, how do you find extreme values?
By first finding critical numbers!
The theorem states that a critical number of a function f is a number c in the domain such that f’ (c) = 0 or f’ is undefined.
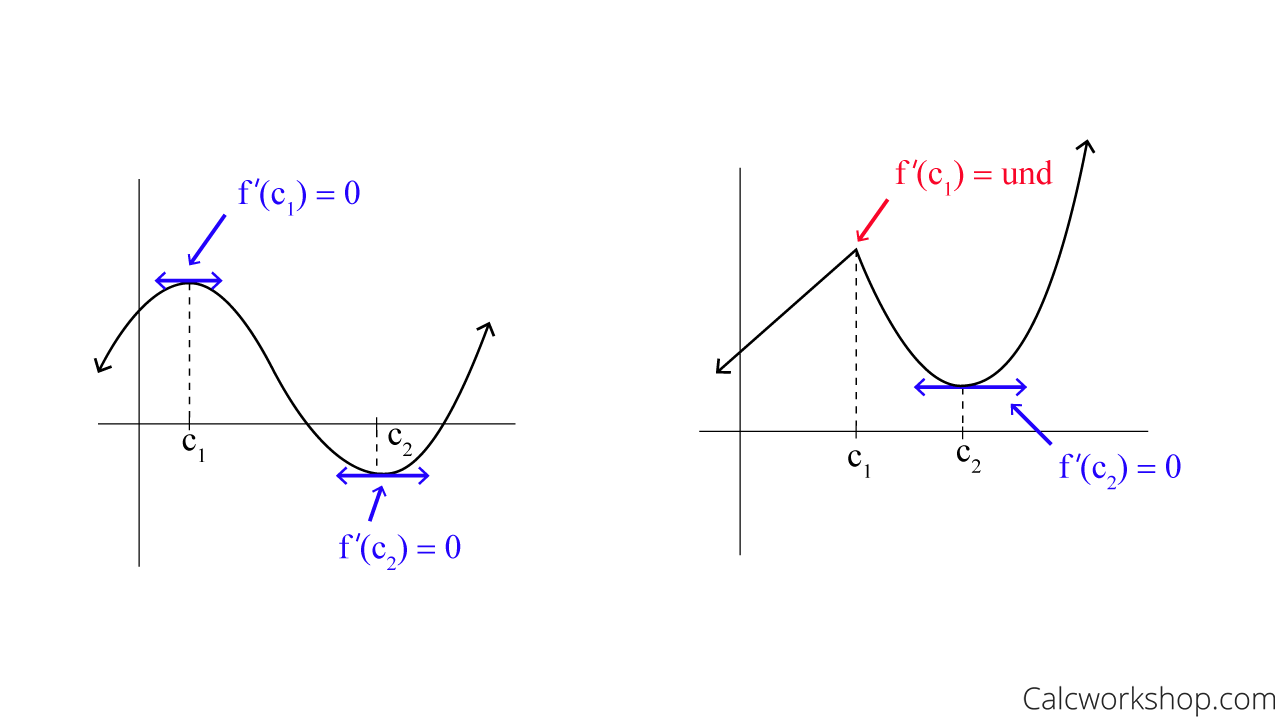
How To Find Critical Points
Ah, this means that when the derivative of a function is zero or undefined, there is a potential maximum or minimum value!
Great, but how does this help us find absolute extrema?
Well, it’s really quite simple.
Steps For Finding Absolute Extrema
Use the following process for finding absolute extrema of a continuous function on a closed interval [a,b]:
- Find all critical numbers of f in the open interval (a,b).
- Evaluate f at each critical number and at both endpoints.
- The smallest value is the absolute minimum, and the largest value is the absolute maximum.
Worked Out Example
For example, suppose we want to find the following function’s global maximum and global minimum values on the indicated interval.
\begin{equation}
f(x)=3 x^{2}-18 x+5,[0,7]
\end{equation}
First, we find all possible critical numbers by setting the derivative equal to zero.
\begin{equation}
\begin{array}{l}
f^{\prime}(x)=6 x-18 \\
6 x-18=0 \\
x=3
\end{array}
\end{equation}
Now we substitute the critical number and both endpoints into the function to determine absolute extrema.
\begin{equation}
\begin{array}{l}
f(3)=3(3)^{2}-18(3)+5=-22 \\
f(0)=3(0)^{2}-18(0)+5=5 \\
f(7)=3(7)^{2}-18(7)+5=26
\end{array}
\end{equation}
See, wasn’t that easy?
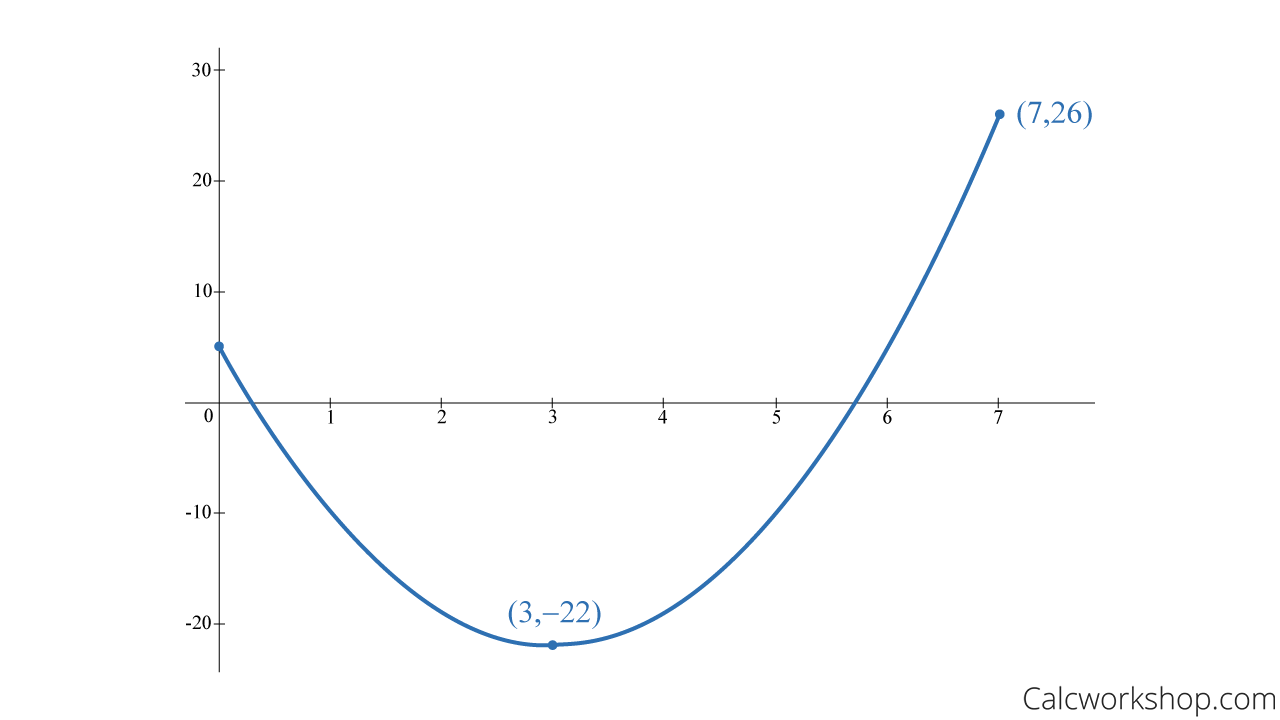
Absolute Extrema – Continuous Function Example
Okay, so together, we will begin our lesson exploring various graphs to locate both global and relative extrema. Then we will identify critical numbers by investigating the first derivative, and then we will use our knowledge to find all absolute extrema on a given interval.
Awesome! Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.