Did you know that inverse trig derivatives are sometimes referred to as the derivatives of arc-functions?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
For example, arcsin is the same thing as sin^(-1). Just as there are synonyms for different words in the English language, there are synonyms in math.
Inverse Trig Functions
And if we recall from our study of precalculus, we can use inverse trig functions to simplify expressions or solve equations.
For instance, suppose we wish to evaluate arccos(1/2).
First, we will rewrite our expression as cosx = 1/2.
Next, we will ask ourselves, “Where on the unit circle does the x-coordinate equal 1/2?”
Then, using our left-hand trick, we arrive at the answer of pi/3!
So, if inverses are so helpful, then it should be no surprise that they are used extensively in calculus to express the solutions to trig equations.
Circular Functions
But before we can learn the rules for differentiating inverse trig functions, we must first deal with a slight problem — trigonometric functions (circular functions) are not one-to-one.
Again, as we discovered in precalculus, trig functions do not pass the horizontal line test, so they don’t have inverses.
But thankfully, we also learned that if we restrict the domain of these trigonometric functions, we can create a one-to-one function, thus allowing us to find inverses!
All we have to do is focus on a portion of the graph that passes the horizontal line test (i.e., the parts that are in red), as seen in the images for sine, cosine, and tangent below.
Graphs – Sin Vs. ArcSin
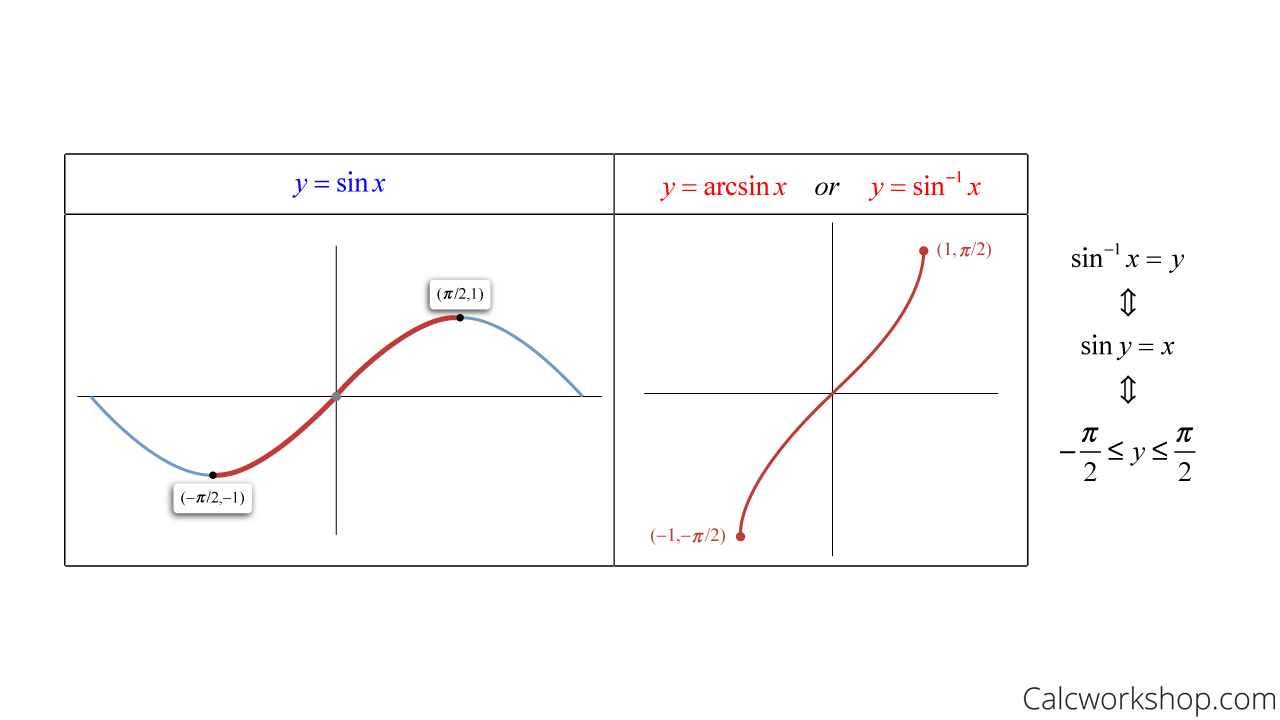
Sinx Vs Arc Sinx – Graph (Properties)
Graphs – Cos Vs. ArcCos
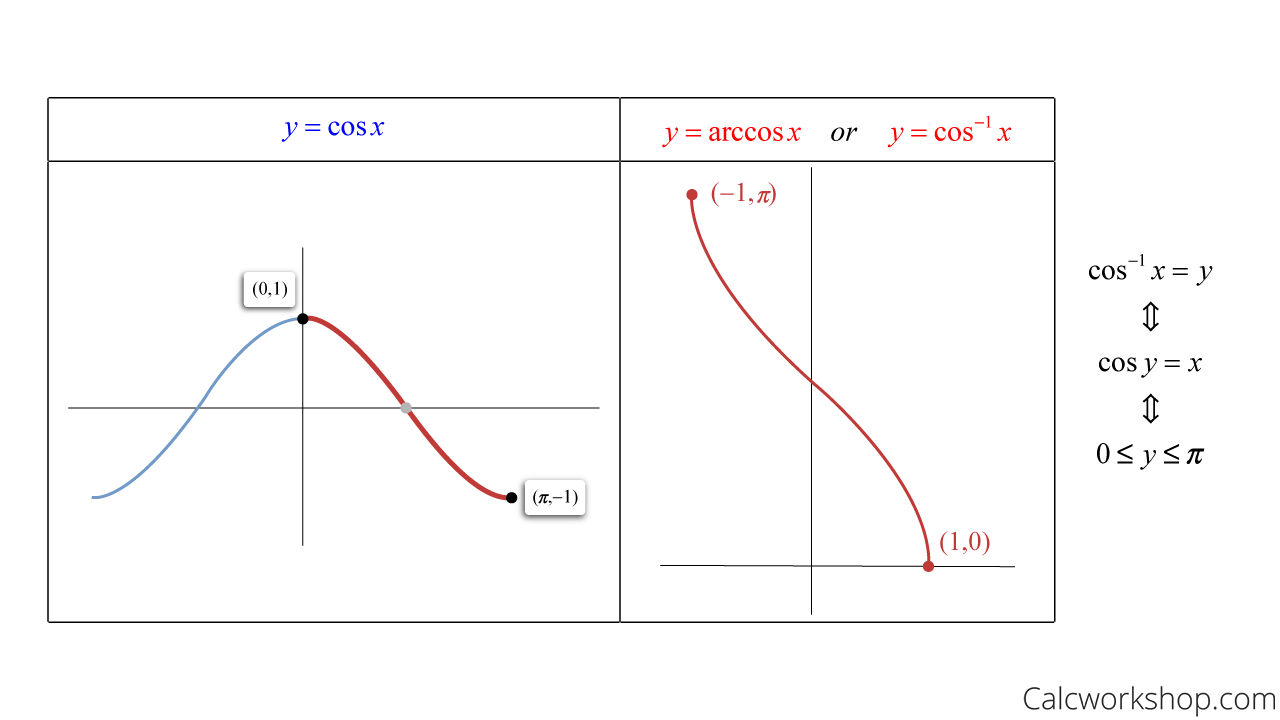
Cosx Vs Arc Cosx – Graph (Properties)
Graphs – Tan Vs. ArcTan
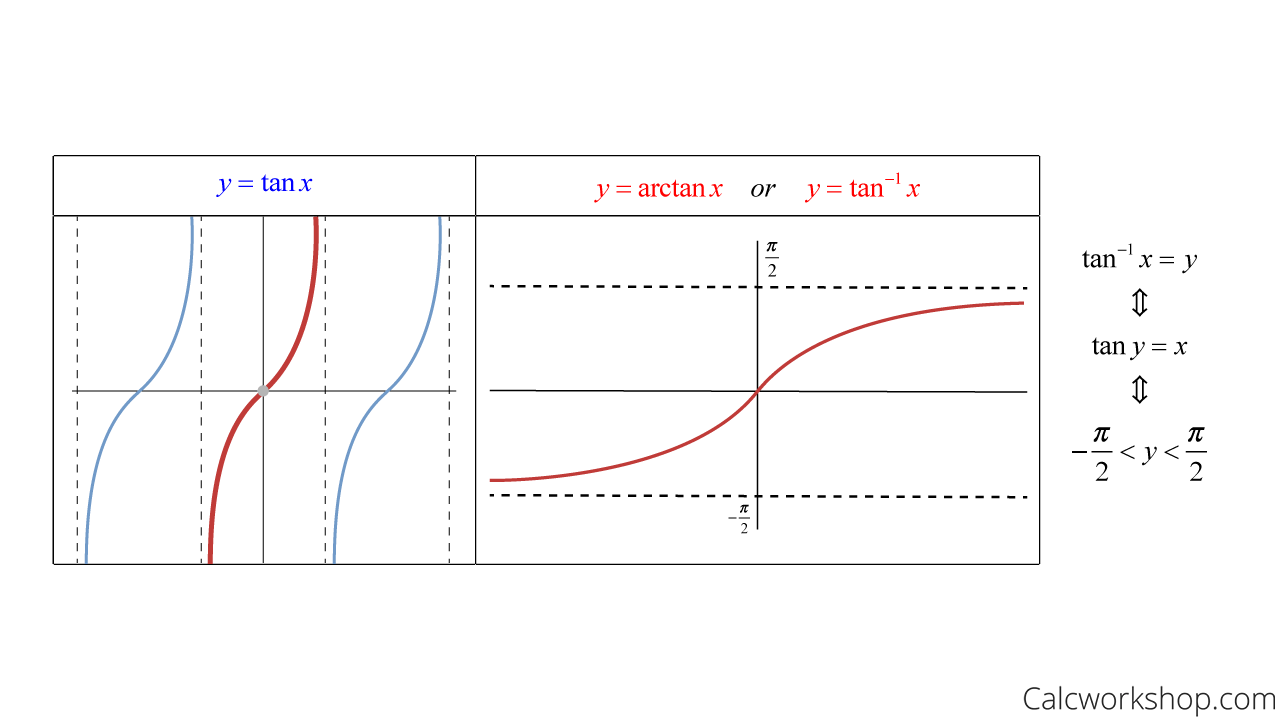
Tanx Vs Arc Tanx – Graph (Properties)
How To Find Inverse Trig Derivatives
Okay, so now that we know that we are only using the restricted domains for sine, cosine, and tangent, we can now calculate the derivatives for these inverse trigonometric functions!
Here is the table of derivatives for inverse trigonometric functions:
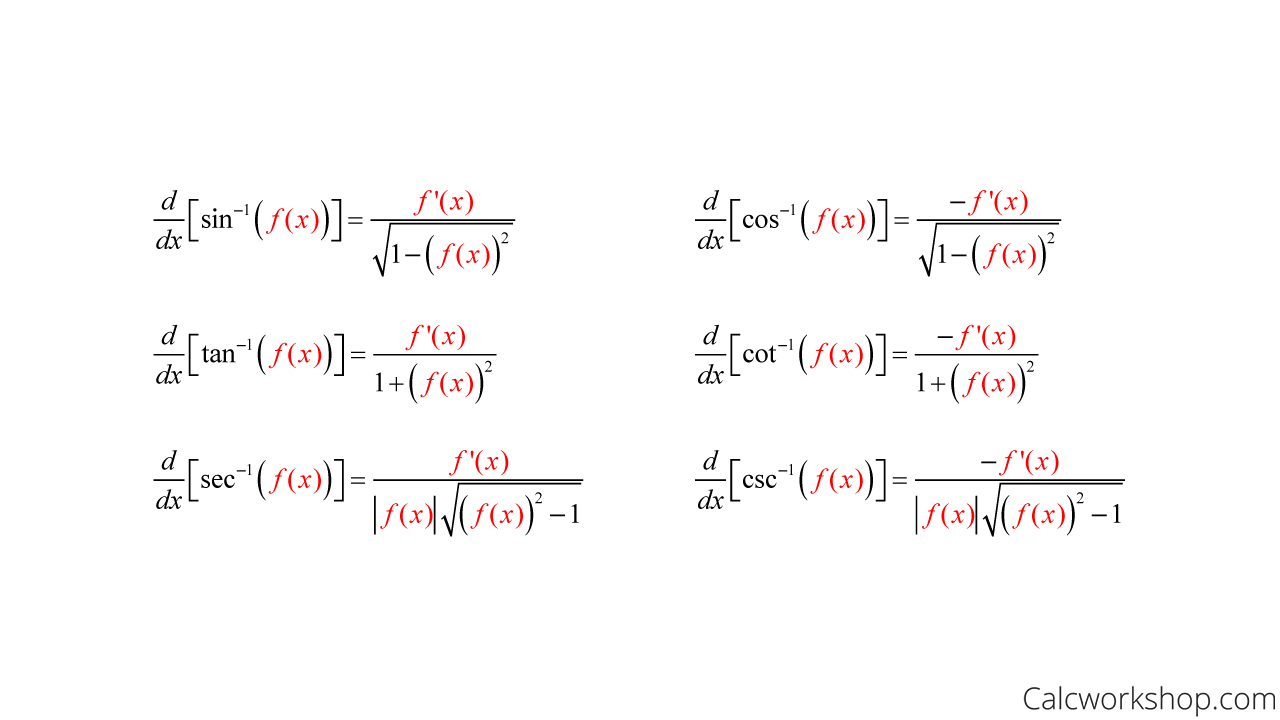
Derivatives Of Inverse Trig Functions
Arcsin Derivative (Proof)
But, before we work on a few examples, I want to take a moment to walk through the steps for proving the differentiation rule for y = arcsin(x).
Why?
Because these new derivative rules seem a little strange at first, as most of them contain square roots, so it’s essential to know where they come from, as it will make them feel less scary.
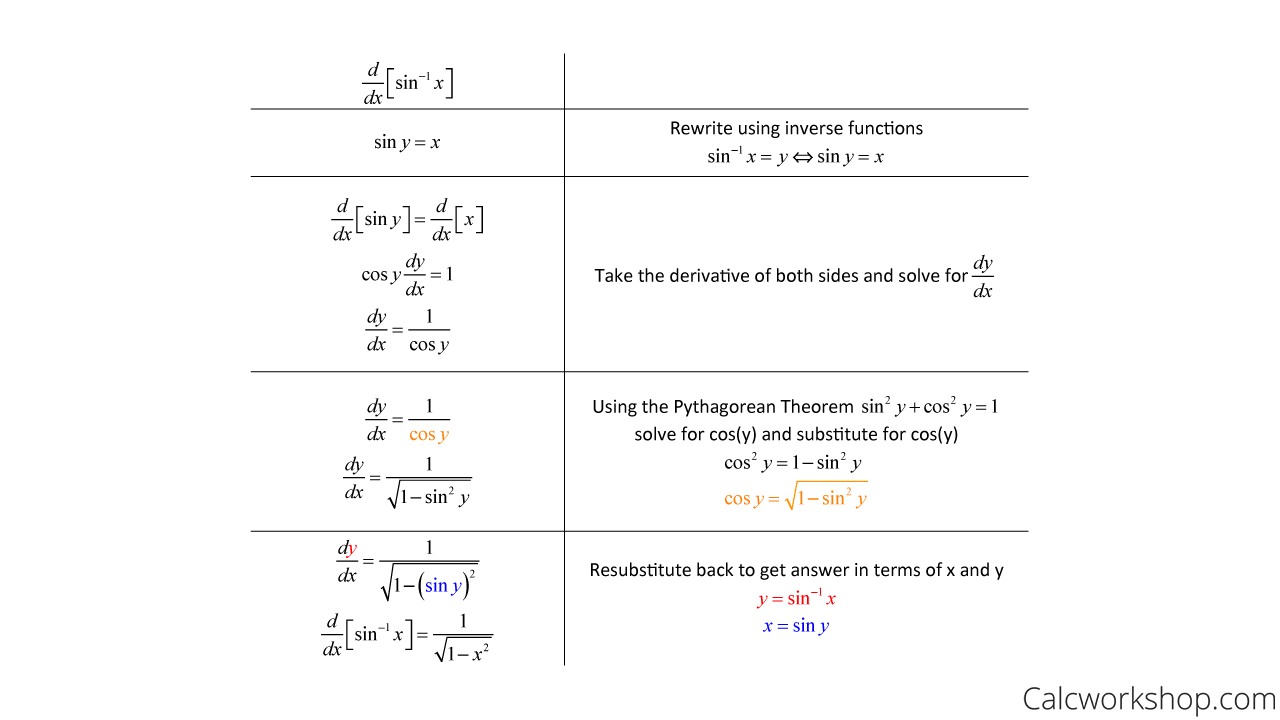
Derivative Of Arcsin – Proof
See how the Pythagorean Identity helped us in a big way!
But thankfully, we don’t need to derive each formula, as we can use the table of differentiation rules for inverse trig functions.
Examples
Now, let’s look at a few examples to see how these derivative rules work.
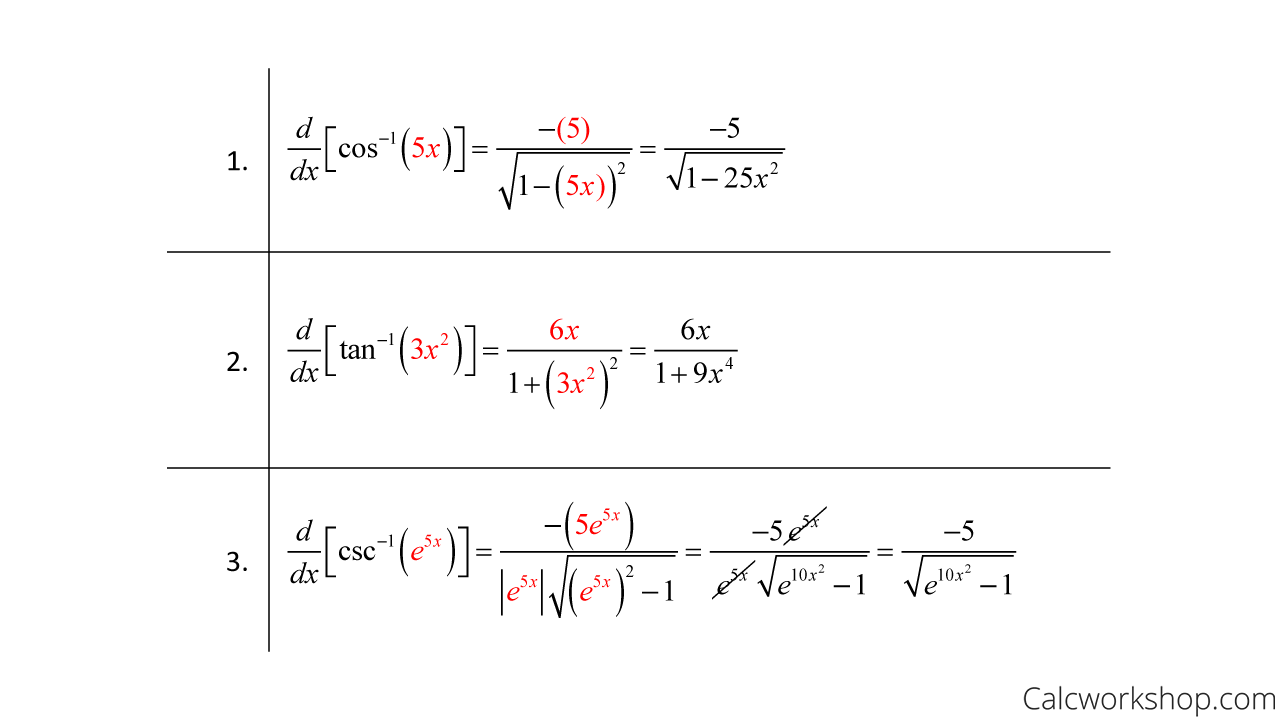
Derivatives Of Arc Trig Functions – Worked Out Examples
Summary
So, as long as we know our formulas, all we have to do is plug in and simplify!
And while the formulas may take a bit of time to get used to, I hope you can see a pattern that is very similar to regular trig derivatives, as well as the connections these rules have with the derivative rules for the other transcendental functions (i.e., exponential and logarithmic).
Together, we will walk through numerous examples in detail to better understand how to apply these derivative rules.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.