Derivatives & Integrals Of Vector Functions
How To w/ Examples!

How do we differentiate and integrate vectors?

How do we calculate the velocity and acceleration of a particle moving in space involving both magnitude and direction?

Thankfully, the same methods and techniques we used in single-variable calculus (i.e., differential calculus) still apply and allow us to define motion along a curve in a plane or space!

So, the calculus of vector-valued functions is largely concerned with how to find their respective derivatives and integrals, this in turn helps us answer questions related to:

• Velocity
• Acceleration
• Speed
• Curvature
• And More

Limit Of A Vector

You will quickly find that the methodology for evaluating the limit of a vector-valued function, which we learned in our previous lesson, can be applied to the calculus of space curves pertaining to derivatives and integrals.

If \(\vec{r}^{\prime}(t) \) is a vector function, then its derivative is defined as \(\frac{d \vec{r}}{d t}=\vec{r}^{\prime}(t)=\lim _{h \rightarrow 0} \frac{\vec{r}(t+h)-\vec{r}(t)}{h}\).

Vector Derivative

Which means, that if we write the vector function in component notation, denoted \(\overrightarrow{r(t)}=\langle f(t), g(t), h(t)\rangle\), where \(f\), (g\), and (h\) are differentiable functions, then \(\vec{r}^{\prime}(t)=\left\langle f^{\prime}(t), g^{\prime}(t), h^{\prime}(t)\right\rangle\).

Let’s see how easy this is by looking at an example.

Example – 1st & 2nd Derivatives

For instance, let’s calculate both the first, \(\vec{r}^{\prime}(t)\), and second derivative, \(\vec{r}^{\prime \prime}(t)\), of the vector-valued function if \(\overrightarrow{r(t)}=\left\langle\cos 2 t, t e^{t}, t-t^{2}\right\rangle\).

All we have to do is differentiate each component of vector \(\vec{r}(t)\).
\begin{equation}
\begin{aligned}
&\vec{r}^{\prime}(t)=\left\langle\frac{d}{d t}[\cos 2 t], \frac{d}{d t}\left[t e^{t}\right], \frac{d}{d t}\left[t-t^{2}\right]\right\rangle \\
&\vec{r}^{\prime}(t)=\left\langle-2 \sin 2 t, t e^{t}+e^{t}, 1-2 t\right\rangle
\end{aligned}
\end{equation}

So, the first derivative is \(\vec{r}^{\prime}(t)=\left\langle-2 \sin 2 t, e^{t}(t+1), 1-2 t\right\rangle\).

Now let’s find the second derivative by differentiating each component of vector \(\vec{r}^{\prime}(t)\).

\begin{equation}
\vec{r}^{\prime \prime}(t)=\left\langle\frac{d}{d t}[-2 \sin 2 t], \frac{d}{d t}\left[e^{t}(t+1)\right]+, \frac{d}{d t}[1-2 t]\right\rangle
\end{equation}

\begin{equation}
\vec{r}^{\prime \prime}(t)=\left\langle-4 \cos 2 t, e^{t}(t+2),-2\right\rangle
\end{equation}

And that’s it. Nothing to it!

Vector Differentiation Rules

And the differentiation rules for the real-valued function (i.e., the component functions (f\), (g\), and (h\) of the vector) are similar for the vector-valued function, as seen below in the following theorem.

Suppose \(\vec{a}\) and \(\vec{b}\) are differentiable vector functions, \(c\) is a scalar, and \(f\) is a real-valued function, then.

\begin{equation}
\begin{gathered}
\frac{d}{d t}[\vec{a}(t)+\vec{b}(t)]=\vec{a}^{\prime}(t)+\vec{b}^{\prime}(t) \\
\frac{d}{d t}[c \vec{a}(t)]=c \vec{a}^{\prime}(t) \\
\frac{d}{d t}[f(t) \vec{a}(t)]=f(t) \vec{a}^{\prime}(t)+\vec{a}(t) f^{\prime}(t) \\
\frac{d}{d t}[\vec{a}(t) \cdot \vec{b}(t)]=\vec{a}^{\prime}(t) \cdot \vec{b}(t)+\vec{a}(t) \cdot \vec{b}^{\prime}(t) \\
\frac{d}{d t}[\vec{a}(t) \times \vec{b}(t)]=\vec{a}^{\prime}(t) \times \vec{b}(t)+\vec{a}(t) \times \vec{b}^{\prime}(t) \\
\frac{d}{d t}[\vec{a}(f(t))]=f^{\prime}(t) \vec{a}^{\prime}(f(t))
\end{gathered}
\end{equation}

Vector Integration

And the definite integral of a continuous vector function is comparable to the definite integral of a continuous real function.

If \(\overrightarrow{r(t)}=\langle f(t), g(t), h(t)\rangle\), then \(\int_{a}^{b} \vec{r}(t) d t=\left\langle\int_{a}^{b} f(t) d t, \int_{a}^{b} g(t) d t, \int_{a}^{b} h(t) d t\right\rangle\).

So, just like derivatives of vector functions, all we have to do to find the definite integral of vector function is to integrate each component function separately.

Example – Definite Integrals

Evaluate \(\int_{0}^{2} \vec{r}(t) d t\) if \(\overrightarrow{r(t)}=\left\langle\cos 2 t, t e^{t}, t-t^{2}\right\rangle\).

To find the definite integral of the vector function, all we have to do is apply the fundamental theorem of calculus to each component function.

\begin{equation}
\int_{0}^{2} \vec{r}(t) d t=\langle\int_{0}^{2}(\cos 2 t) d t, \underbrace{\int_{0}^{2}\left(t e^{t}\right) d t}_{\begin{array}{c}
\text { use integration } \\
\text { by parts }
\end{array}}, \int_{0}^{2}\left(t-t^{2}\right) d t\rangle
\end{equation}

\begin{equation}
=\left.\left\langle\frac{1}{2} \sin 2 t, t e^{t}-e^{t}, \frac{1}{2} t^{2}-\frac{1}{3} t^{3}\right\rangle\right|_{0} ^{2}
\end{equation}

\begin{equation}
=\left\langle\frac{1}{2} \sin (4), 1+e^{2},-\frac{2}{3}\right\rangle
\end{equation}

See, evaluating an integral of a vector function is just as easy as differentiating!

Example – Indefinite Integrals

But what if we are given an indefinite integral? How do we find the antiderivative?

We simply integrate each component and add a “+C”

So, using our previous example, suppose \(\overrightarrow{r(t)}=\left\langle\cos 2 t, t e^{t}, t-t^{2}\right\rangle\).

Evaluate \(\int \vec{r}(t) d t\).

\begin{equation}
\int \vec{r}(t) d t=\langle\int(\cos 2 t) d t, \underbrace{\int\left(t e^{t}\right) d t}_{\begin{array}{c}
\text { use integration } \\
\text { by parts }
\end{array}}, \int\left(t-t^{2}\right)\rangle
\end{equation}

\begin{equation}
=\left\langle\frac{1}{2} \sin 2 t+C_{1}, t e^{t}-e^{t}+C_{2}, \frac{1}{2} t^{2}-\frac{1}{3} t^{3}+C_{3}\right\rangle
\end{equation}

Easy!

Alright, so evaluating the derivative and integral of a vector function is pretty straightforward, but what is the purpose of doing so?

To describe motion in a plane or space!

Unit Tangent Vector

Well, the geometric meaning of the derivative \(\vec{r}^{\prime}(t)\) is that \(\vec{r}^{\prime}(t)\) is tangent to the curve and the length of \(\vec{r}^{\prime}(t)\), denoted \(\left\|\vec{r}^{\prime}(t)\right\|\), is the speed. And since \(\vec{r}^{\prime}(t)\) points in the direction of motion and its length is the speed, we can call \(\vec{r}^{\prime}(t)\) the velocity vector and \(\vec{r}^{\prime \prime}(t)\) the acceleration vector.

And a particle whose position vector at the time \(t\) is \(\vec{r}(t)\) having velocity \(\vec{r}^{\prime}(t)\) and speed \(\left\|\vec{r}^{\prime}(t)\right\|\), the unit vector in the direction of \(\vec{r}^{\prime}(t)\) is:

\begin{equation}
T(t)=\frac{\vec{r}^{\prime}(t)}{\left\|\vec{r}^{\prime}(t)\right\|}
\end{equation}

This unit vector, \(T(t)\), called the Unit Tangent Vector, records the direction of motion.

Example

For example, if \(\overrightarrow{r(t)}=\left\langle\cos 2 t, t e^{t}, t-t^{2}\right\rangle\) let’s find the unit tangent vector at the point where \(t=0\).

Step 1

First, we will need to find \(\vec{r}^{\prime}(t)\). Thankfully, we calculated this earlier and found:

\begin{equation}
\vec{r}^{\prime}(t)=\left\langle-2 \sin 2 t, e^{t}(t+1), 1-2 t\right\rangle
\end{equation}

Step 2

Next, we will evaluate the velocity vector at the point where \(t=0\).

\begin{equation}
\vec{r}^{\prime}(0)=\left\langle-2 \sin 2(0), e^{0}(0+1), 1-2(0)\right\rangle=\langle 0,1,1\rangle
\end{equation}

Step 3

Now we will need to calculate the speed of \(\vec{r}(t)\) when \(t=0\), which is the magnitude of the velocity vector \(\vec{r}^{\prime}(0)\).

\begin{equation}
\left\|\vec{r}^{\prime}(0)\right\|=\sqrt{(0)^{2}+(1)^{2}+(1)^{2}}=\sqrt{2}
\end{equation}

Step 4

Now, let’s substitute our values into the unit tangent formula:

\begin{equation}
T(t)=\frac{\vec{r}^{\prime}(t)}{\left|\vec{r}^{\prime}(t)\right| \mid}
\end{equation}

\begin{equation}
T(0)=\frac{\vec{r}^{\prime}(0)}{\left|\vec{r}^{\prime}(0)\right| \mid}=\frac{\langle 0,1,1\rangle}{\sqrt{2}}=\left\langle 0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right\rangle
\end{equation}

Easy, right?

So, together we will learn how to find derivatives and integrals of vector functions and discuss the definition of smooth curves in 3-space. Additionally, we will represent the tangent vector, unit tangent vector, and antiderivative of vector-valued functions while given initial conditions.

There’s a lot to uncover, so let’s jump right in!

Video Tutorial w/ Full Lesson & Detailed Examples (Video)

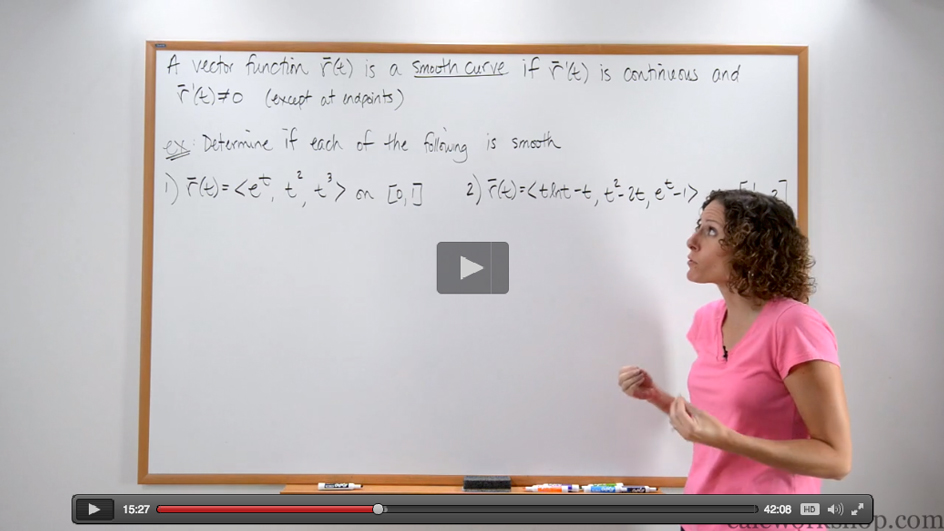
Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.