Did you know that the limit of a function helps us define continuity?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
As we’ve previously seen in our study of limits, a function is continuous if its graph can be drawn without picking up your pencil.
In other words, there are no gaps in the curve.
But while it may be obvious to the viewer who is looking at a graph to determine whether or not a function is continuous, a diagram isn’t considered to be sufficient or definitive proof.
How To Prove Continuity
So, how do we prove that a function is continuous or discontinuous?
A two-step algorithm involving limits!
Formally, a function is continuous on an interval if it is continuous at every number in the interval. Additionally, if a rational function is continuous wherever it is defined, then it is continuous on its domain.
Again, all this means is that there are no holes, breaks, or jumps in the graph. Otherwise, the function is considered discontinuous.
Recall that there are four types of discontinuity:
- Removable
- Infinite
- Jump
- Oscillating
The first three are the most common and the ones we will be focusing on in this lesson, as illustrated below.
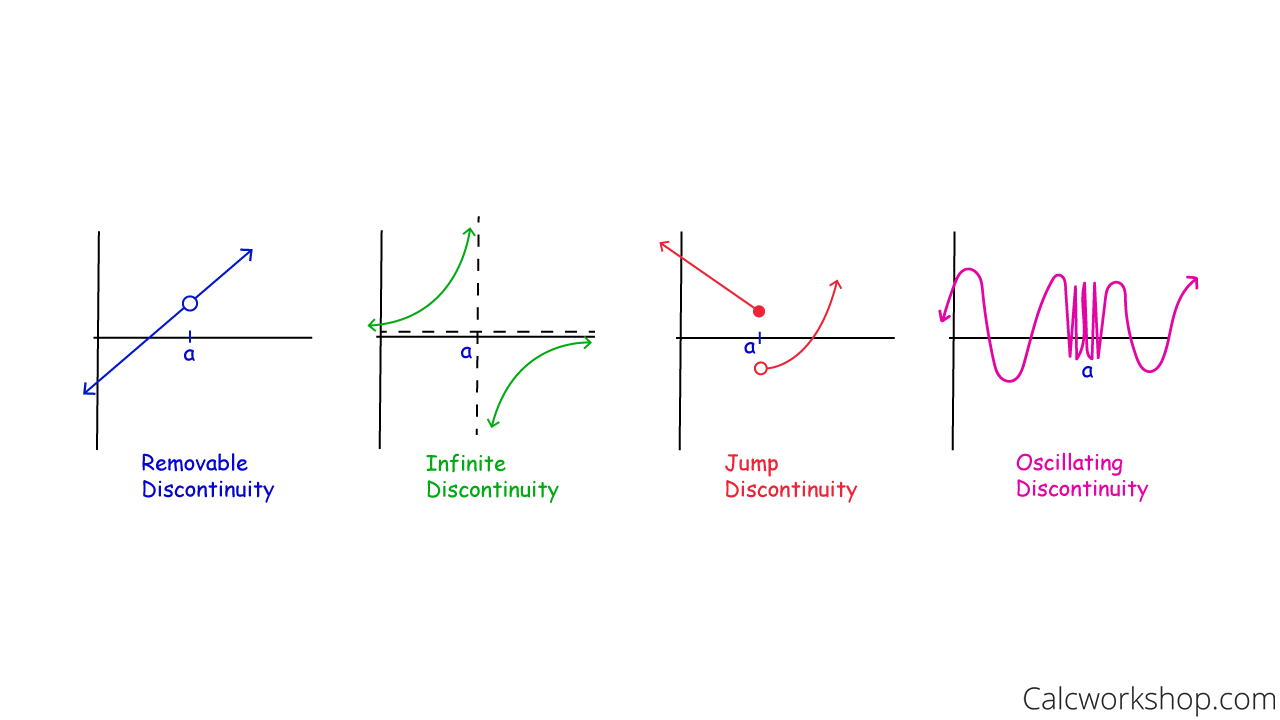
4 Types Of Discontinuity
- Limit exists as x approaches a.
- The function is defined at x = a.

Continuity Test Calculus
Continuous
For example, let’s prove that the following function is continuous.

How To Prove A Function Is Continuous
And this brings us to an important fact: Polynomial functions, Rational functions, Root functions, and Trigonometric functions are continuous at every number in their domains.
If f and g are continuous at a, and c is a constant, then the following functions are also continuous.

Properties Of Continuous Functions
Discontinuous
But what happens if a function is not continuous?
Will our algorithms still work? Yes!
Here’s how.
For example, let’s verify the following function is discontinuous using our two-step method.

How To Prove A Function Is Discontinuous
See. It’s pretty straightforward, and here’s what so amazing…
…Continuity is one of our gateways to understanding functions and the rate of change (i.e., derivatives).
Intermediate Value Theorem
In fact, as Paul’s Online Notes nicely states, with our understanding of limits and continuity, we can comprehend such concepts as the intermediate value theorem, which states that if you have two points connected along a continuous curve, then there is a point in-between.
Suppose that f is a continuous function on the closed interval [a,b] and let M be any number between f(a) and f(b). Then there exists a number c in (a,b) such that f(c) = M
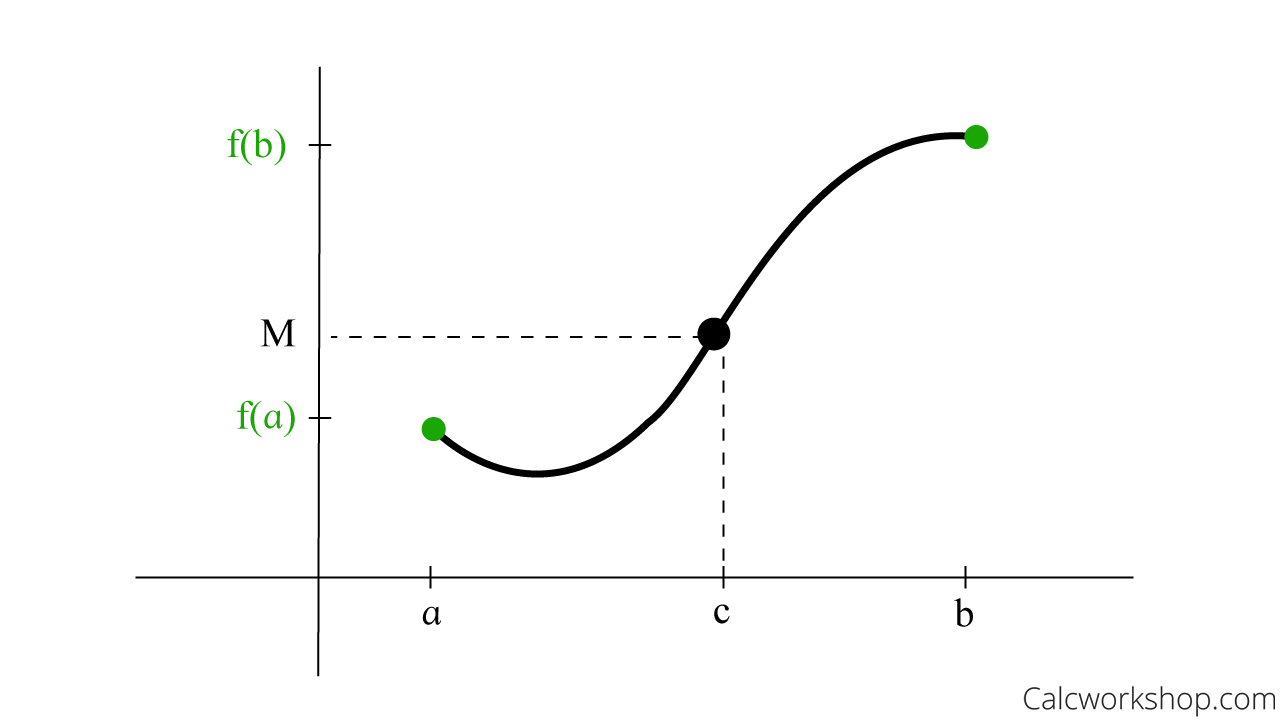
Intermediate Value Theorem — Definition
This means that if we have a closed interval and the function is continuous, so there are no gaps or holes or breaks, then we are guaranteed to find some x-value, c, within the interval with a y-value M, also within the interval.
Summary
Together we will begin our lesson by reviewing continuity and exploring the three types of discontinuity: jump, point (removable discontinuity), and infinite.
Then we will learn how to prove a function is continuous or discontinuous by applying a two-step algorithm involving limits.
So, let’s get started.
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.