What if I told you that there was a really easy way to remember the quotient rule for derivatives?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Anything to make calculus easier right?
Well then, let’s go!
What Is The Quotient Rule
The quotient rule is a method for differentiating problems where one function is divided by another.
The premise is as follows:
If two differentiable functions, f(x) and g(x), exist, then their quotient is also differentiable (i.e., the derivative of the quotient of these two functions also exists).
Discovered by Gottfried Wilhelm Leibniz and Isaac Newton, the formula goes like this:
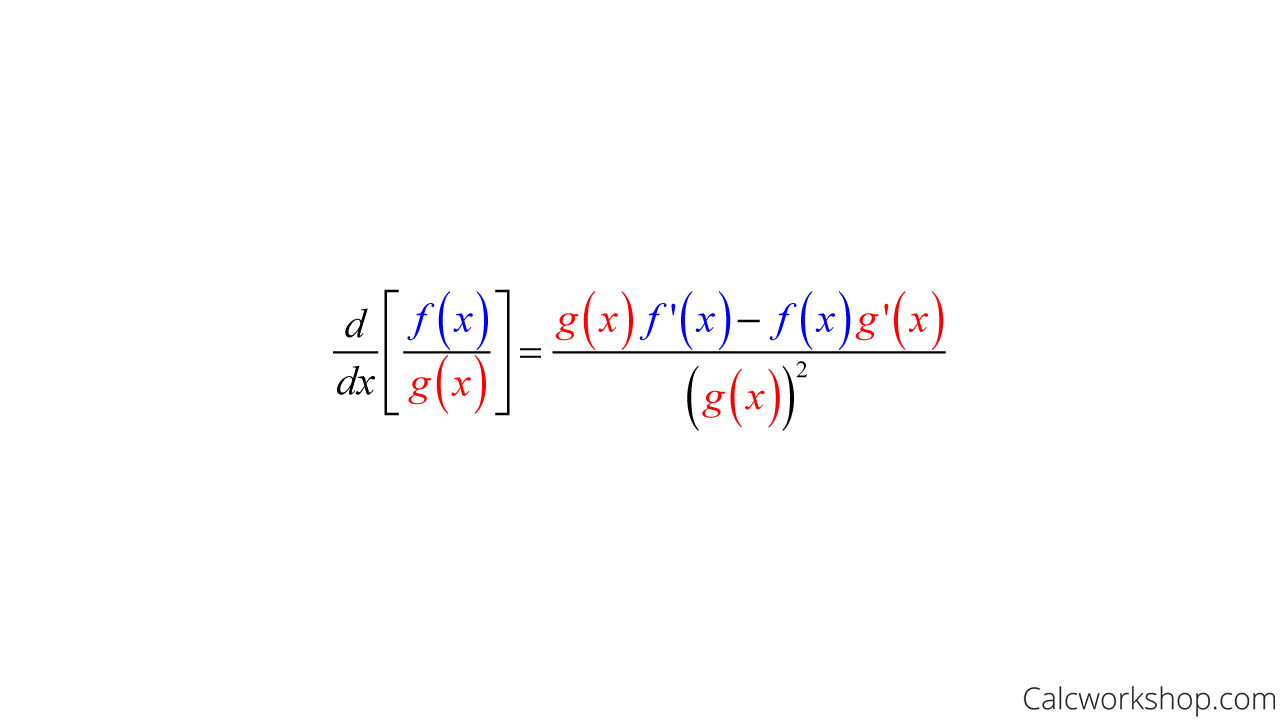
Quotient Rule Formula
Fun Mnemonic – Hi Dee Ho
Now, I have to admit that this formula looks a bit intimidating at first, but there’s an easy pattern to help us remember it and a fun saying that makes memorizing the steps super easy!
The trick is to always start with the bottom function and end with the bottom function squared. I like to call this function “Ho” because it’s “low,” and that means the top function is called “Hi” because it’s “high up.”
So, the saying goes something like this — Ho-Dee-Hi minus Hi-Dee-Ho over Ho-Ho!

Quotient Rule Mnemonic
See, isn’t it fun to say?
The “Dee” represents the derivative of the function, as the quotient rule is formally read as the bottom times the derivative of the top, minus the top times the derivative of the bottom, all divided by the bottom squared.
But let’s be honest, it’s much more fun to say “HoHo” than “bottom squared,” am I right?
Quotient Rule Examples
As always, it’s best to see how this formula works in practice, so let’s look at an example where we will use the quotient rule to differentiate the function below.
Ex) Derivative Of A Fraction
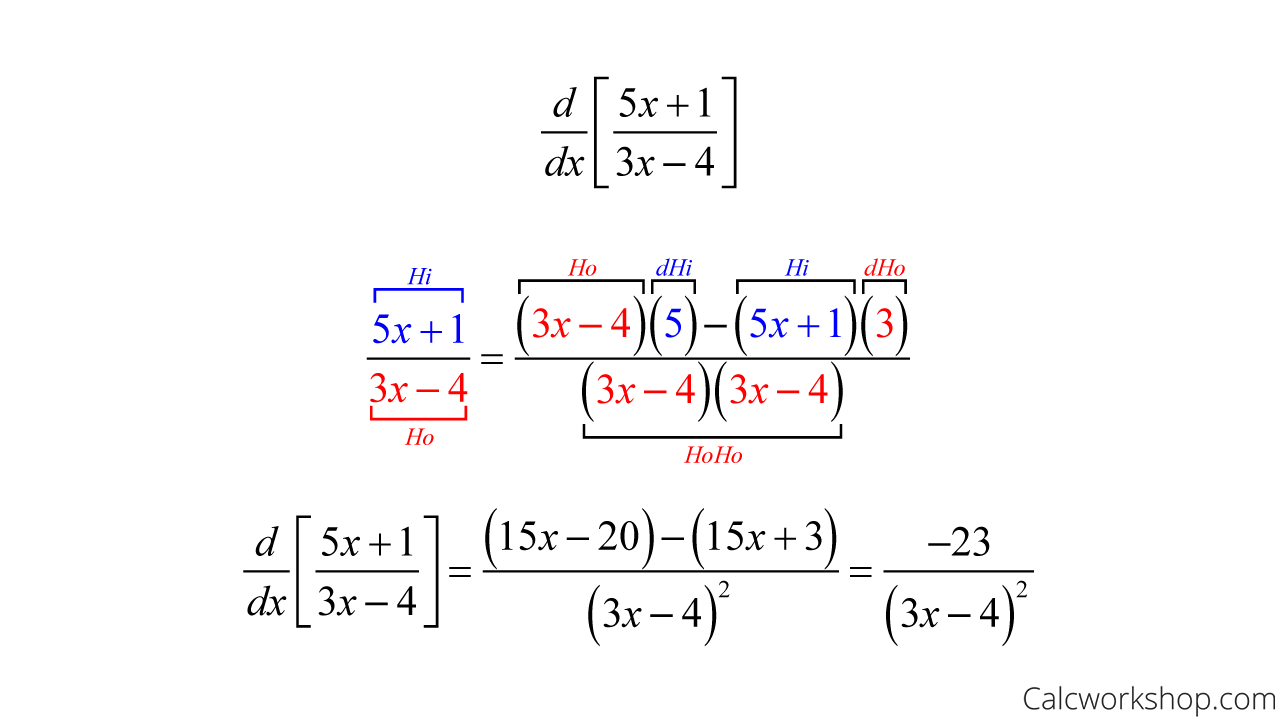
Quotient Rule Derivative
Ex) Common Mistake
And just as we saw with the product rule, I want to caution you and help you to avoid a common mistake.
The derivative of a quotient is not equal to the quotient of the derivatives, as the example below nicely demonstrates.
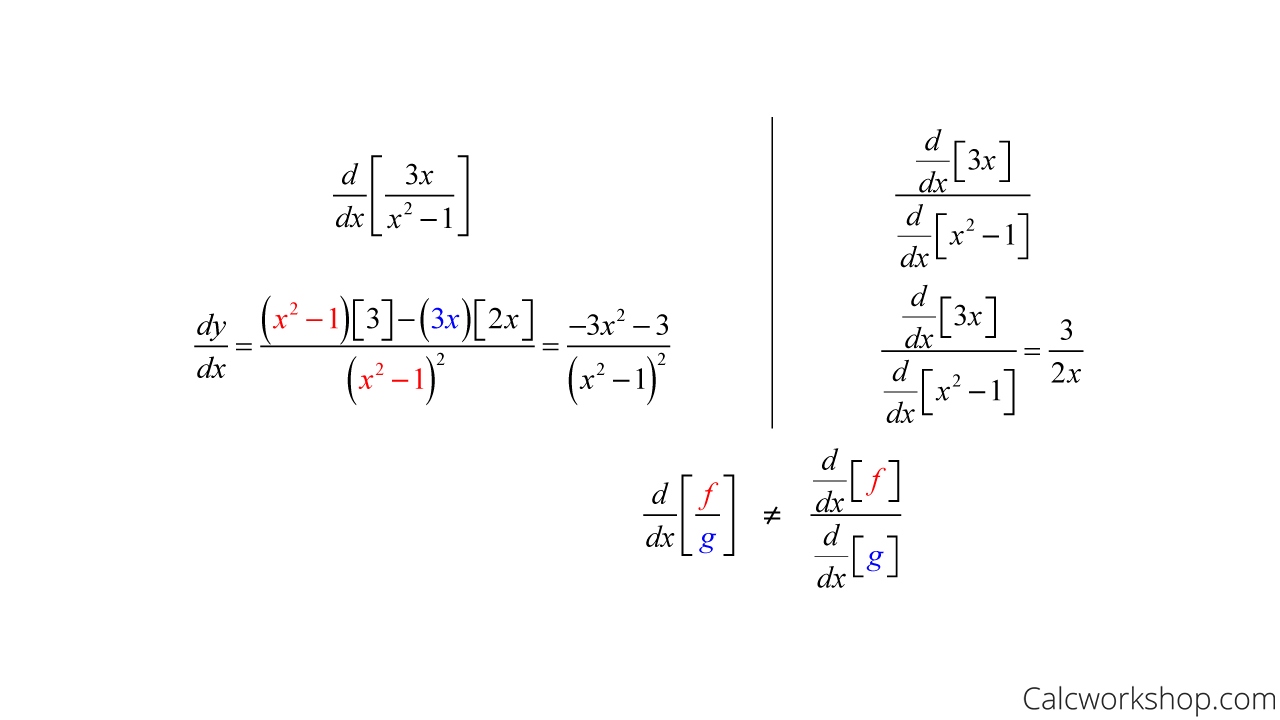
The Derivative Quotient Does NOT Equal The Quotient Derivative
What is so interesting about this derivative rule is how closely it relates to our understanding of the product rule, except for a minus instead of a plus.
But there is a small warning. While the quotient rule is super easy to remember, thanks to our fun saying, as Paul’s Online Notes so accurately states, the numerator of the quotient rule is very similar to the product rule. So please take your time and check your signs!
Ex) Instantaneous Rate Of Change
Let’s look at another example so you can get more comfortable with this new differentiation rule.
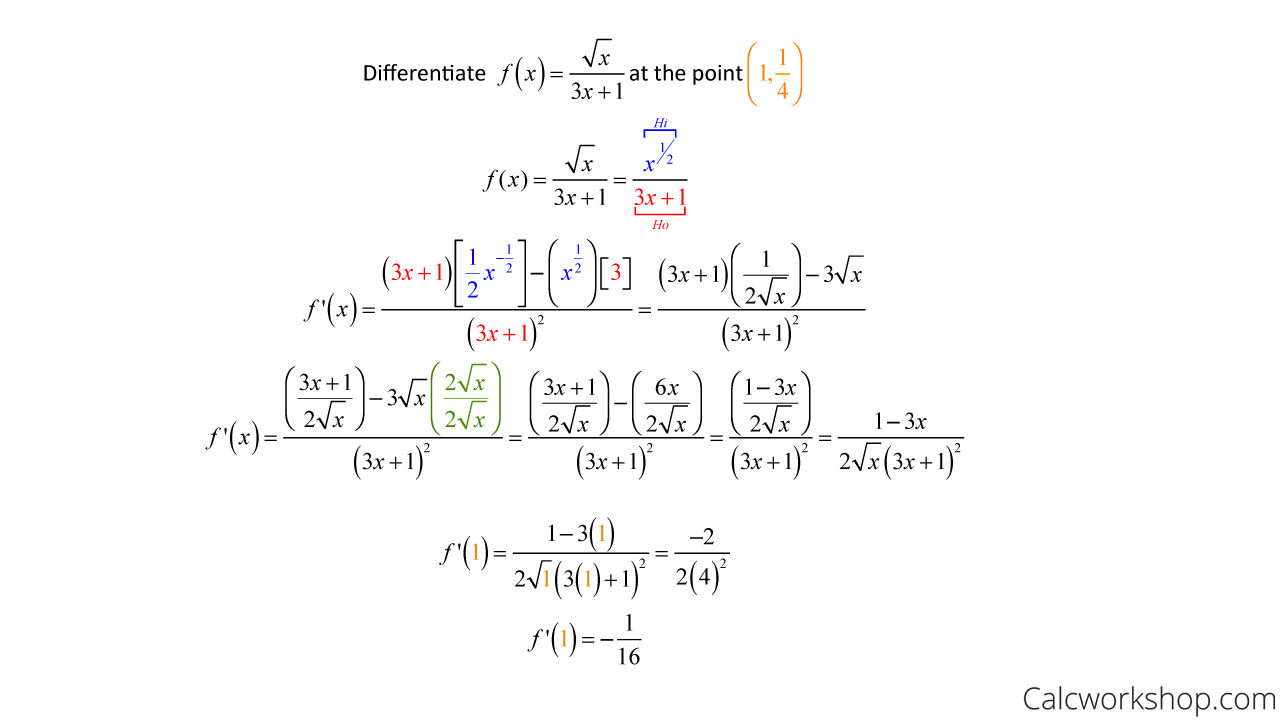
Evaluate The Derivative Of The Function At The Given Point
So, we just found the instantaneous rate of change for f(x) when x = 1, all thanks to our new rule!
Cool, huh?
Together we will work through several examples in detail, color coding, and chanting our fun Ho-dee-Hi jingle along the way, so you will quickly master this fantastic rule. And we will look at how to quotient rule helps us find the rate of change, or instantaneous velocity, of one function divided by another.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.