There are certain types of differential equations for which an explicit solution is attainable.
And the technique we will use is called separation of variables.
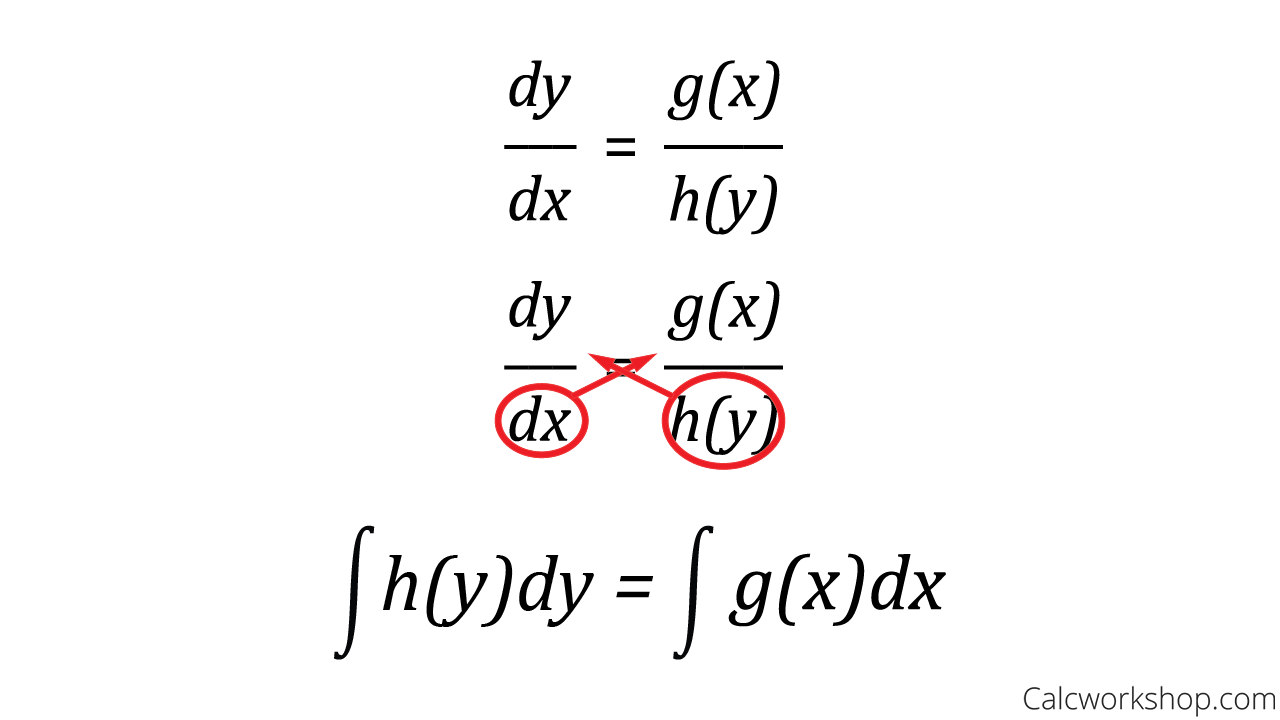
How to Separate Variables
In fact, there are only four basic steps for solving these first-order differential equations, in which the expression for the slope can be factored or separated into a function of x times a function of y.
In other words, we are going to be given a derivative where all the x’s and y’s are intermixed (i.e., implicit differentiation) and we are going to have separate and integrate the x values and y values separately.
Paul’s Online Notes, emphasizes this fact when stating that for a differential equation to be separable, all the y’s in the differential equation must be multiplied by the derivative, and all the x’s in the differential equation must be on the other side of the equal sign.
We will begin by learning the steps for solving a separable equation and then practice by solving nine different examples.
Together, we will solve for the General Solution, the Particular Solution given an initial constraint, and remember how to use our algebra skills to simplify our answers given exponents.
Separable Differential Equations Video

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.