Did you know that the derivative and antiderivative of an exponential function are strikingly similar?
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In fact, the only difference is whether we multiply or divide the coefficient!
Let’s take a look.
Derivative of an Exponential Function
In our derivatives lessons, we learned the three easy steps for taking the derivative of an exponential function:
- Rewrite
- Multiply by the natural log of the base
- Multiply by the derivative of the exponent
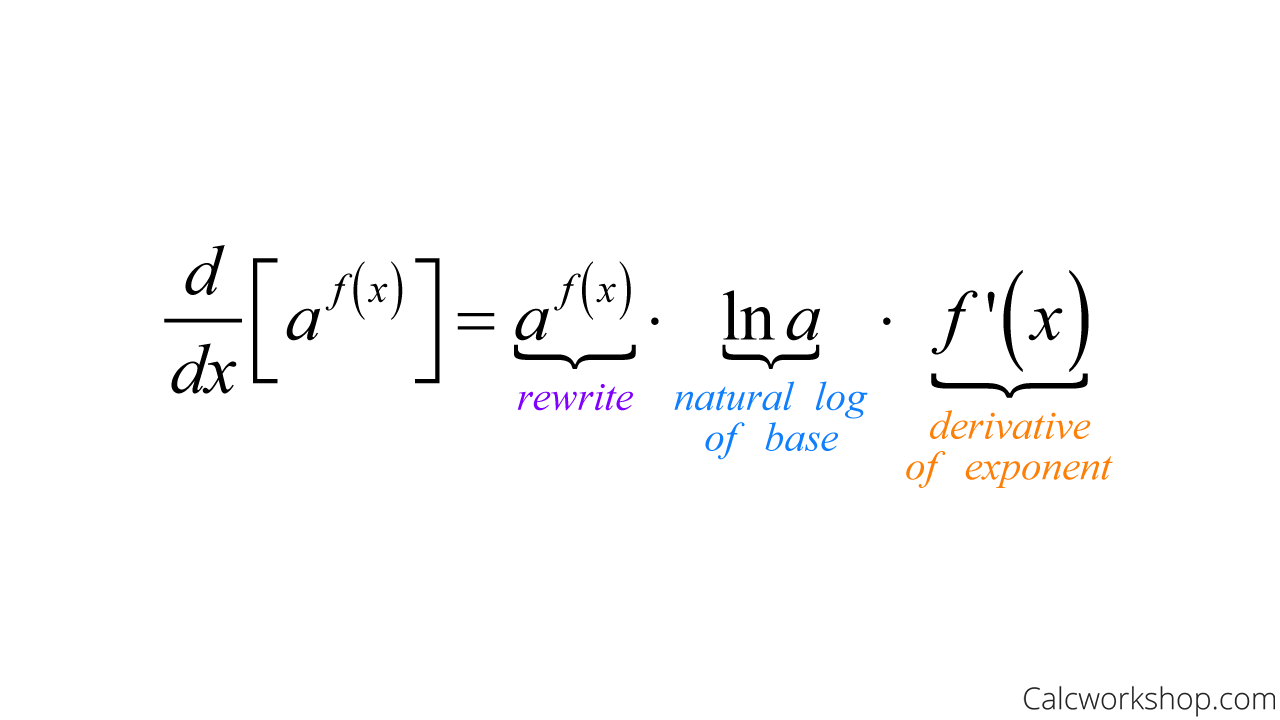
Derivative Of Exponential
Antiderivative (Integral) of an Exponential Function
Well, to find the antiderivative (integral) of an exponential function, we will apply the same three steps, except instead of multiply, we will divide!
- Rewrite
- Divide by the natural log of the base
- Divide by the derivative of the exponent
\begin{equation}
\int \color{red}a^{\color{blue}b \color{black}x} \, \color{black}d x = \frac{\color{red}a^{\color{blue}b \color{black}x}}{\color{blue}b(\color{black}\ln \color{red}a\color{black})} + \color{black}C
\end{equation}
\(\color{red}a\): The base of the exponential function.
\(\color{blue}b\): The constant that multiplies the variable ‘x’ in the exponent. This coefficient determines the growth or decay rate of the exponential function.
\(\frac{1}{\color{blue}b(\color{black}\ln \color{red}a\color{black})}\): The term that is the division of the derivative of the exponent and the natural log of the base.
Integrating Exponential Functions with Base ‘e’
But what happens if the base ‘a‘ is Euler’s number ‘e‘? Do we need a different formula?
So glad you asked!
You will find that the most common base in calculus is the irrational number e.
e=2.718281828459045…
But here’s what is so amazing!
The process of integrating base e functions is exactly the same as integrating any other exponential curve. The only difference is that we can simplify the result.
How?
By remembering that the natural log of e is equal to one: ln(e) = 1.
\int \color{red}a^{\color{blue}b \color{black}x} \color{black}d x = \frac{\color{red}a^{\color{blue}b \color{black}x}}{\color{blue}b\color{black}(\ln \color{red}a\color{black})}+\color{black}C
\end{equation}
\begin{equation}
= \frac{\left(\color{red}a^{\color{blue}b}\color{black}\right)^{\color{black}x}}{\color{blue}b\color{black}(\ln \color{red}a\color{black})}+\color{black}C
\end{equation}
\int \color{red}e^{\color{blue}b \color{black}x} \color{black}d x = \frac{\color{red}e^{\color{blue}b
\color{black}x}}{\color{blue}b(\color{black}\ln \color{red}e\color{black})}+\color{black}C
\end{equation}
\begin{equation}
= \frac{\color{black}1}{\color{blue}b} \color{red}e^{\color{blue}b \color{black}x}\color{black}+\color{black}C
\end{equation}
And that’s why base e is the “natural choice” in calculus!
Now, it must be noted that the derivative of the exponent must be a constant for us to use this rule. If the derivative of the exponent is something other than a constant (number), then we will have to utilize more advanced integration techniques, which we will learn about in future lessons.
Alright, so let’s look at a few examples to help see how easy this formula is to use.
Examples of Integrating Exponential Functions
Problem #1
Evaluate \(\int e^{2 x} d x\)
All we have to do is identify the pieces of the integrand and match them to our formula.
\int e^{2 x} d x
\end{equation}
\begin{equation}
=\frac{e^{2 x}}{2(\ln e)}+C
\end{equation}
\begin{equation}
=\frac{1}{2} e^{2 x}+C
\end{equation}
\int \color{red}e^{\color{blue}b \color{black}x} \, \color{black}d x
\end{equation}
\begin{equation}
= \frac{\color{red}e^{\color{blue}b \color{black}x}}{\color{blue}b(\color{black}\ln \color{red}e\color{black})}+\color{black}C
\end{equation}
\begin{equation}
= \frac{\color{black}1}{\color{blue}b} \color{red}e^{\color{blue}b \color{black}x}\color{black}+\color{black}C
\end{equation}
Simple, right?
Let’s look at another example.
Problem #2
Evaluate \(\int 4^{-x} d x\)
Okay, so once again, we just need to identify the pieces of the integrand and match them to our formula and simplify.
\begin{equation}
\int 4^{-1 x} d x
\end{equation}
\begin{equation}
=\frac{4^{-1 x}}{-1(\ln 4)}+C
\end{equation}
\begin{equation}
=\frac{\left(4^{-1}\right)^x}{-1(\ln 4)}+C
\end{equation}
\begin{equation}
=\frac{-\left(\frac{1}{4}\right)^x}{(\ln 4)}+C
\end{equation}
See! Nothing to it.
Applications of Exponential Functions
While it is most certainly cool how the exponential function is its own derivative and integral, why is the antiderivative of exponential functions important?
Because it has an amazing connection to Power Series and the Laplace Transform.
At the end of Calculus 2, you will learn about power series and Taylor polynomials. And you will learn how the exponential function’s power series plays a significant role in understanding convergence.
And for those continuing in their math education, a widely used tool in engineering and applied mathematics is the Laplace Transform, where the integration of exponential functions stars in a key role.
Next Steps
In the video, you’ll…
- Practice integrating various indefinite and definite integrals involving exponential functions to build your skills.
- Use your knowledge of exponent and logarithmic properties to simplify integrands and solutions effectively.
- Dive in and start working through examples to gain a deeper understanding of integrating exponential functions.
Video Tutorial w/ Full Lesson & Detailed Examples
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.