Calculus is a subject that many people find intimidating. Some students are scared to take their first calculus class, and others might be terrified by the prospect of teaching themselves.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
The good news is that there’s no need to worry!
Because after teaching calculus for the past 15 years, I’m going to give you the best way to approach learning the material.
Let’s go…
Why Learn Calculus?
In some cases, the decision may have already been made for you…
- As in order to pursue higher-level science and engineering courses, you will need calculus, as it is required.
- If it’s just a challenge you crave, perhaps you just want to prove to yourself that you can do it.
- Or maybe you have a passion for math, and you want the adventure of learning a new ‘language.’
With that said…
…did you know that few people realize the beauty and power of calculus. This branch of mathematics is one of the most important and widely used branches in the world. It enables us to understand change in various real-world situations, finds maxima and minima, optimizes functions, and understands rates of change.
For instance, Youtube and TikTok employ calculus in their algorithms to determine which video should be displayed next by optimizing for view time.
In addition, optimization strategies are used by FedEx and UPS to get shipments to you on time. And don’t forget hedge funds studying stock market behavior (i.e., how things change over time).
Whether it’s for school, a career, or simply because you’re interested in learning more about the world around you, I’m a firm believer that anybody can learn calculus if they have access to the proper tools and resources.
So, Where Do I Start?
If you’re gearing up to learn calculus this semester, then you’ll need a few essential tools.
First and foremost, you’ll need a graphing calculator. This is an absolute must for doing any sort of math, but it will be especially important in calculus class. The TI-89 is my personal favorite. However, if your professor doesn’t allow the 89, you may use a TI-84+ or computer software like Mathematica instead.
However, if you’re learning on your own or just need extra resources, then I would suggest obtaining a James Stewart Calculus book (any edition) as it’s the most widely used calculus text available and contains great examples and practice problems.
And finally, if you want to get the most out of your learning experience, it’s always helpful to have someone who can teach you directly — preferably in person! But if that’s not an option, you’ll be happy to know that there are lots of great calculus video series available online.
How Long Will It Take?
Keep in mind that everyone learns differently and at different speeds. Don’t get discouraged if you don’t understand something right away – just take a step back, review the material, and try again.
What Is The Big Picture Of Calculus?
It’s the course that makes all your other math classes make sense — maybe for the first time.
But Calculus does more than just explain patterns and relationships between algebra, geometry, trigonometry and the countless formulas we were forced to memorize, it also explains real-world phenomena.
- How to evaluate and solve equations and formulas.
- Graph a line on the coordinate plane.
- And understand slope as the rate of change.

Plotting Points And Graphing A Line
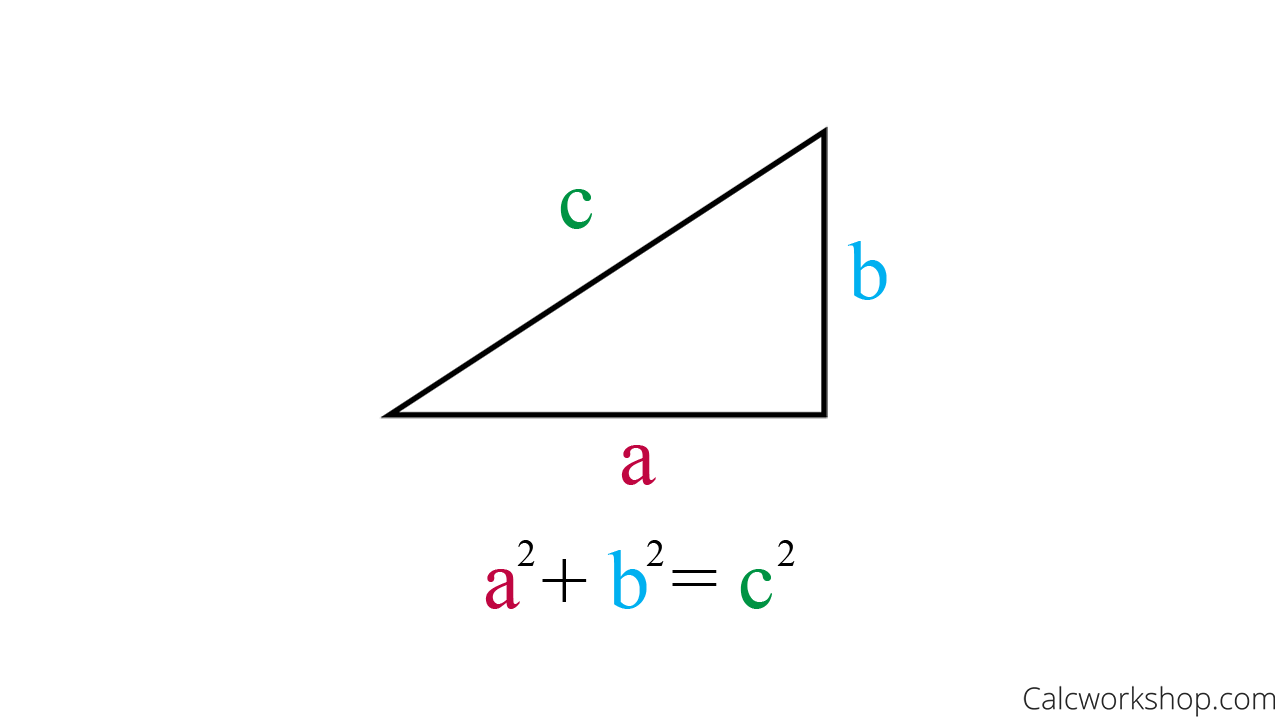
Pythagorean Theorem – Formula
And we saw how trigonometric identities and properties helped to describe motion and waves along with vector projection.
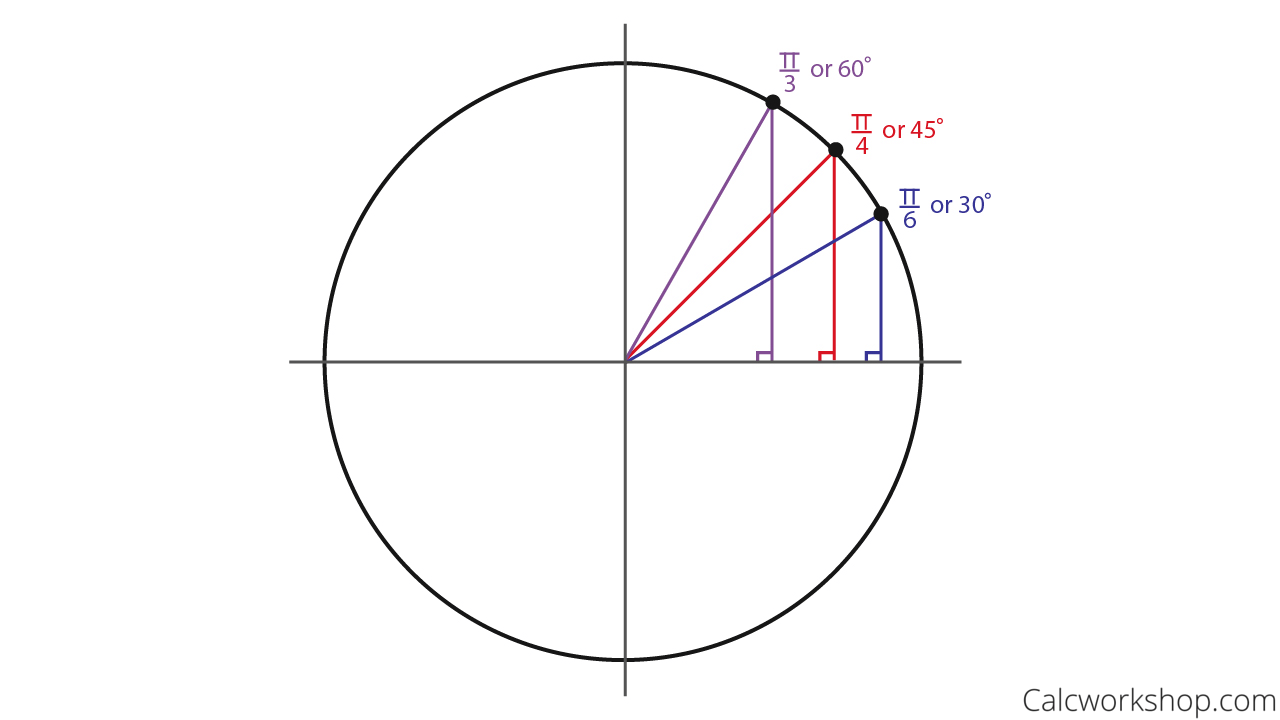
Unit Circle with Special Right Triangles
But did you know that our knowledge of slope, area, and trigonometric ratios can all be explained using calculus? And how calculus is the glue that links all of these incredible ideas and topics together?
It’s true!
So, if Calculus can explain why we learned the skills we gained in previous courses, maybe we should know a bit more about what it entails?
Alright, so there are only three major topics in calculus.
That may surprise you because most people think Calculus is this daunting, vastly complex course. But in reality, it’s just a study of limits, derivatives, and integrals.
Let’s take a quick look at each, so you have a big-picture idea of what Calculus is all about.
The Limit
A limit is the idea of closeness. As we approach a value along the x-axis, what is the y-value approaching?
Formally we say that the limit of a function, f(x), as x approaches some value a, equals L, provided that as we get sufficiently close to a, from both sides without actually equaling a, we can make f(x) as close to L.
Why is this idea of closeness important?
Because a limit allows us to investigate functions without having to be defined and can help us examine asymptotes, continuity, tangent lines, and so much more.
And if you’re the curious type, here’s my introduction video for finding limits graphically.
The Derivative
A derivative measures how a function changes with respect to a variable. It calculates the rate of change, or slope of a function.
Yes, but we only learned about the constant, never changing slope of a line. But what about every other curve out there in the world?
Think about it.
Just driving to the store or school tells you that the road changes and curves, so there has to be a way to measure this, right?
The derivative is equivalent to finding the slope of the tangent line to a curve at a point and helps us explain such things as velocity, acceleration, speed, and distance. Differentiation describes how things change over time.
Integrals
In contrast, integration (also called antidifferentiation) reverses the derivative process to help us understand
- Areas
- Volumes
- Probabilities
- Accumulation
- Displacement
- And Distance
Generally speaking, an integral is a way to calculate the area under a curve.
And by using our previous skills for finding the area and volume of basic geometric shapes such as rectangles and trapezoids, we can determine the area and volume of more complex or oddly shaped regions.
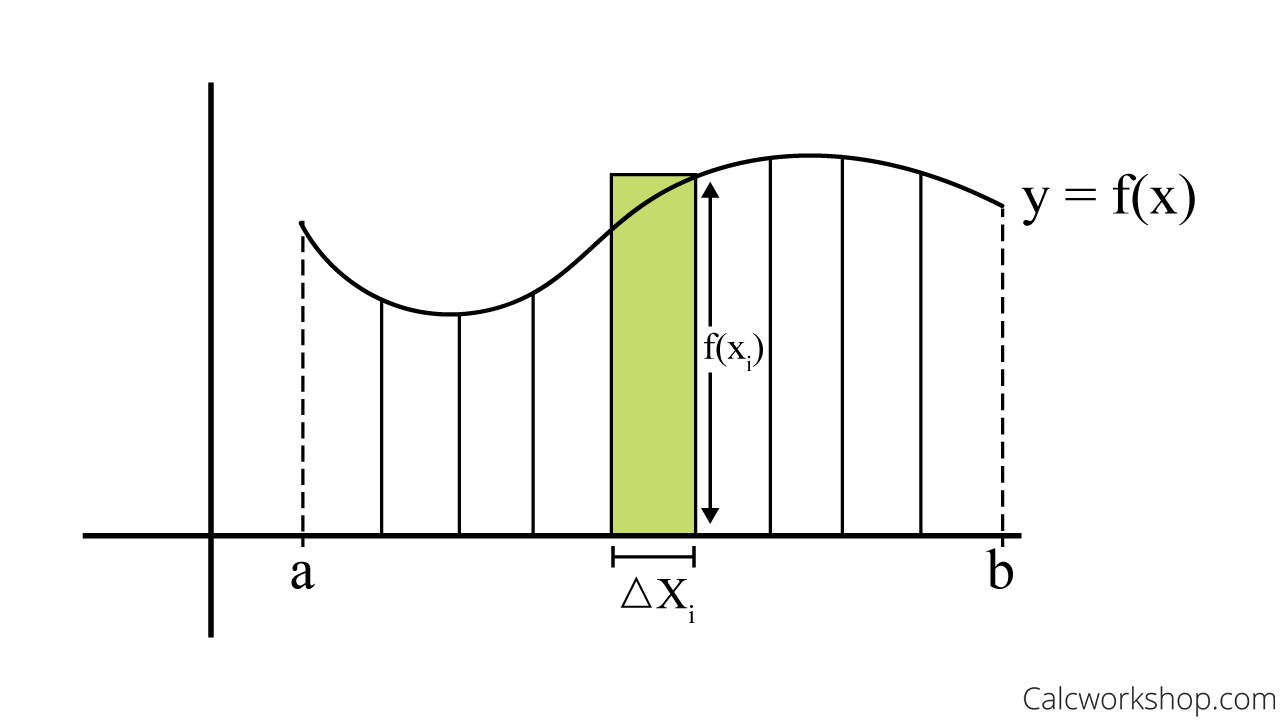
Estimating Area Under A Curve Riemann Sum
Additionally, integration also helps us to determine distance and displacement.
Think of it this way. If differentiation calculates the rate of change over an interval of time and helps us understand such things as velocity and acceleration and speed, then integration does the opposite and helps us find the total distance traveled.
These are the three fundamental ideas in calculus.
As you progress in your studies, you will learn various techniques, formulas, and theorems that will give you a deeper understanding of the subject. Still, everything you learn in calculus will fall under one of these three umbrella concepts.
Some Pitfalls Of Learning Calculus
I’ve been teaching calculus for over 15 years, so I know that it can be a difficult subject to learn. But if I could go back to talk to my former self and share some of the tips I have learned along the way, this is what I would say…
- Don’t Give Up – Even When It’s Hard.
- Find The Right Resources.
- It’s Not The Calculus That Gets You. It’s The Algebra.
- Know Your Functions – It’s Critical!
- How to graph and solve polynomial functions either using the quadratic formula, factoring, or synthetic or long division.
- How to graph and solve exponential and logarithmic functions. You absolutely want to review your exponential and logarithmic properties as you will use them extensively in both engineering calculus and business calculus.
- How to simplify and graph rational functions (i.e., functions with vertical and horizontal asymptotes) to find domain and range.
Your tenacity is what will propel you to succeed in calculus. Yes, there are going to be difficult moments. Yes, you’re going to struggle from time to time. But struggling is not a sign of weakness — it is a sign of participation in a worthy battle.
With any endeavor, you need practice and perseverance. You need to practice in order for the concepts to stick, and you need to be determined enough to keep trying.
You can not master calculus in just a few short hours of cramming before a test. It takes perseverance and daily effort. Learning something new can sometimes feel like an uphill battle, but don’t lose heart and be willing the keep trying.
Remember, you don’t want to be in this situation…
Don’t feel like you are an island unto yourself. Help is available if you know where to look.
The first place to look is your math textbook. In high school, you probably only opened your math textbook to complete the exercise problems at the end of each section. That’s not going to cut it anymore. You actually need to embrace your math textbook, read the sections, and work through the example problems.
And don’t forget about those online resources to help you make sense of those tricky concepts…
…watching a video and seeing someone walk you through a tough problem or even explaining a theorem or definition can make all the difference in the world.

Getting Help At The Campus Tutoring Center
By the time you’ve reached calculus, you have forgotten more math than most people have ever learned. Therefore, it’s possible that you might not remember all those skills you learned along the way.
But never fear. It won’t take long to bounce back and remember all that you have forgotten, so you won’t be left making any more silly algebraic mistakes.
So, what type of algebra skills do I need?
Fractions and Factoring.
I know you’re smiling and rolling your eyes, but hear me out.
You will need to know how to simplify expression continuously in calculus, and the biggest problem students face is how to simply fractions or factor.
Being able to obtain common denominators with polynomials, factor and reduce fractions, solve polynomial equations using factoring or radicals, etc., are all necessary skills in calculus.
Think about it. Calculus is tricky by itself, therefore you don’t need to waste precious brain power trying to remember how to simplify a complex fraction when you should be focusing on how to integrate. Review your basics because it will set you apart from your peers.
Functions play a huge role in calculus. You will not only be expected to know how to solve various functions but you will be required to know how to find their domain and range.
Wait! What’s a function again? And what type of functions are we talking about?
A function is a relation where each input is related to exactly one output. We used the vertical line test to help us determine whether a graph was a function, and we found that for each x-value (domain), there was one y-value (range).
As for the types of functions, you will need to remember:
Reviewing these concepts ahead of time will save you countless hours of frustration and heartache. Remember, calculus is the study of how functions change, so you have to know your functions in order to succeed!
You can pass calculus and avoid these common pitfalls by getting ahead, reviewing your algebra, finding a study group, and never giving up.
Final Thoughts
For anyone who has ever read a challenging book like the Illiad, Plato’s Republic, or a Shakespearean play, you know that task may be challenging at times. But if you stick with it, the understanding and insights you gain are unparalleled. Not to mention the fact that you now have some serious bragging rights.
The same thing is true with learning calculus. Yes, it will take hard work at times, but the numerous benefits you’ll obtain when you master it are unrivaled. It will reveal things to you that are hidden from most people’s eyes.
So, take a deep breath, get started, and be ready to expand your mind.
You’ve got this!
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.


