What if I told you that every time you take a trip to the store, you experience the second derivative test in action?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Let me explain.
Every week, I make a trip to our local grocery store. Along the way, I encounter several traffic lights. If the light ahead has just turned red, I must shift my foot from the gas pedal to the brake so I can slow down and stop.
In the moment my foot makes the switch from the gas to the brake, a point of inflection is created, as it signals my speed changing from fast to slow.
And it’s the second derivative test that is the key to finding these moments of change and helps us confirm whether critical values are maximums or minimums.
Alright, so let’s break down some keywords and get to the bottom of concavity, points of inflection, and the second derivative test.
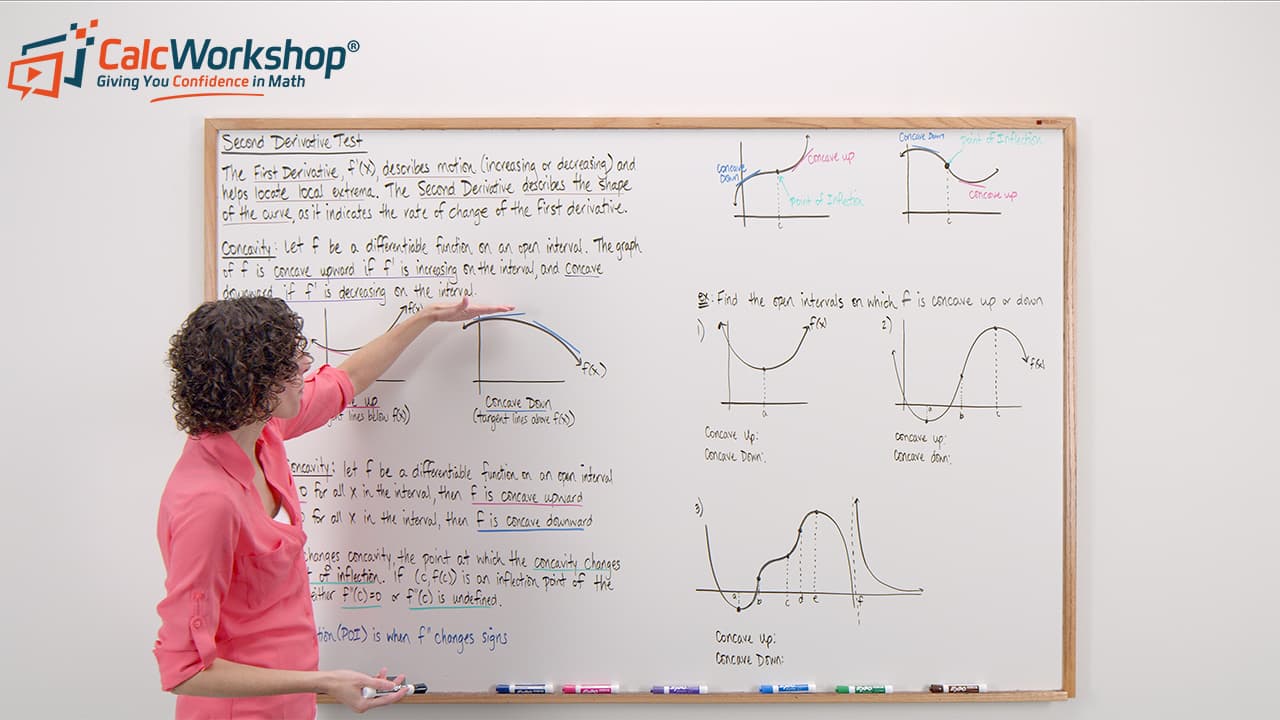
Concavity describes the rate of change of a function’s derivative. If f’ is increasing then the graph is concave up, and if f’ is decreasing, then the graph is concave down.
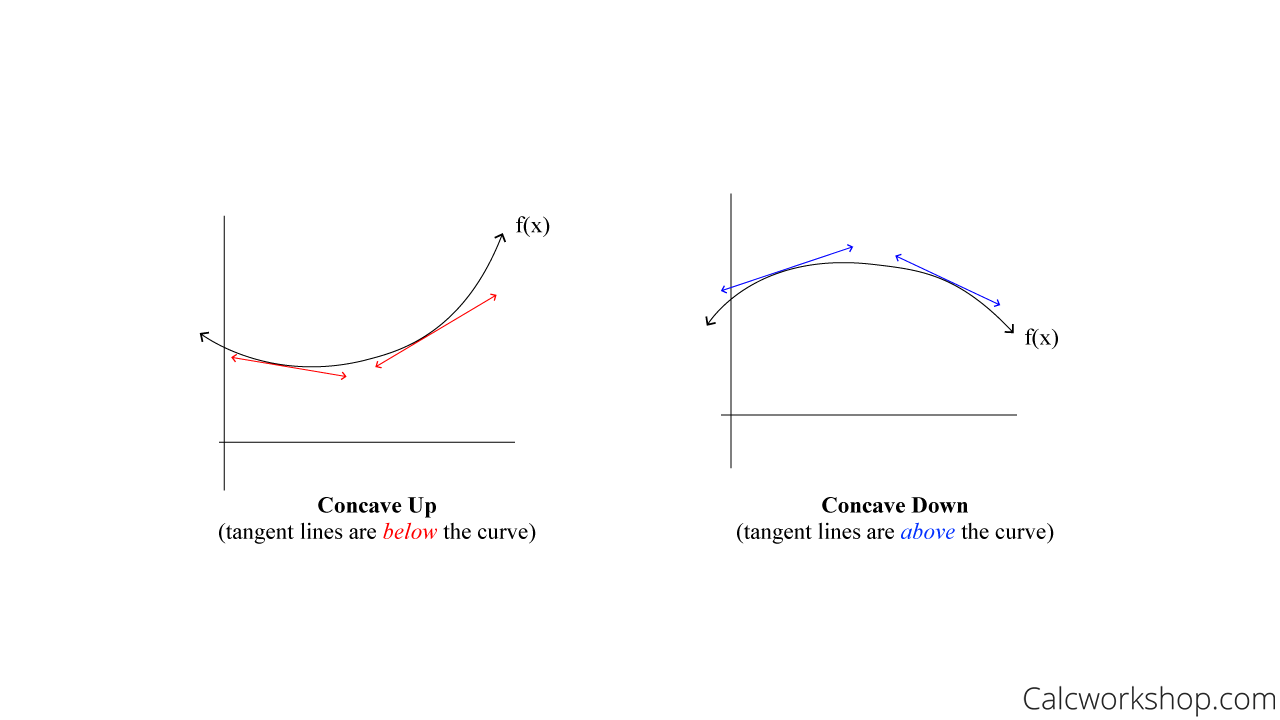
Concave Up And Down
To test for concavity, we have to find the second derivative and determine whether it is positive or negative.
If \(f^{\prime \prime}(x)>0\) for all x in the interval, then f is concave upward.
If \(f^{\prime \prime}(x)<0\) for all x in the interval, then f is concave downward
And if a graph changes concavity, the point at which the concavity changes is called the point of inflection.
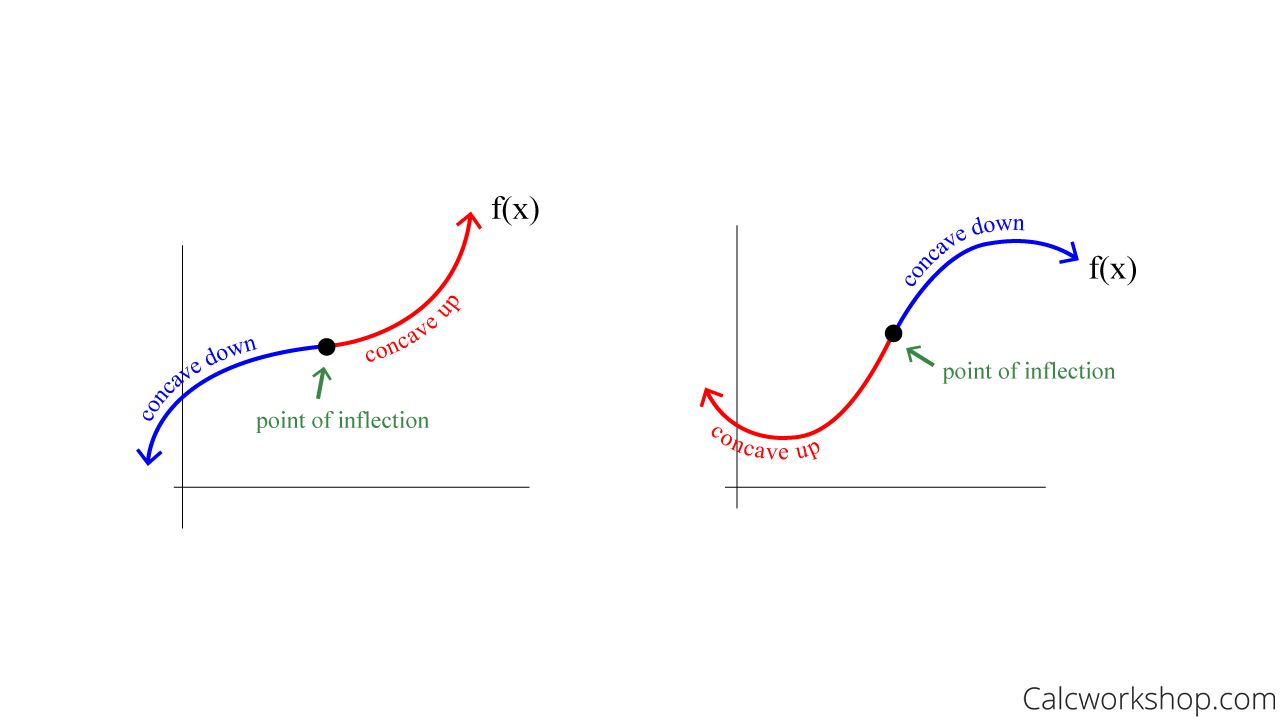
What Is An Inflection Point
Example
So, let’s apply our theorem for testing concavity and find any inflection points with the following example.
Suppose we wish to determine the open intervals on which the graph of f(x) is concave upward or downward as well as any inflection points.
\begin{equation}
f(x)=\frac{x^{3}}{4}-3 x
\end{equation}
First, we must locate the x-values at which \(f^{\prime \prime}(x)=0\) or \(f^{\prime \prime}(x)\) is undefined.
\begin{equation}
\begin{array}{l}
f^{\prime}(x)=\frac{3}{4} x^{2}-3 \\
f^{\prime \prime}(x)=\frac{3}{2} x \\
\frac{3}{2} x=0 \\
x=0
\end{array}
\end{equation}
Next, we will create test intervals. We do this by selecting values to the left and right of this x-value we located into our second derivative and identify whether the sign is positive or negative.
Let’s choose x = -1 and x = 1 for our test intervals.
\begin{equation}
\begin{array}{l}
f^{\prime \prime}(-1)=\frac{3}{2}(-1)=\frac{-3}{2}<0 \\
f^{\prime \prime}(1)=\frac{3}{2}(1)=\frac{3}{2}>0
\end{array}
\end{equation}
Because the sign of the second derivative to the left of zero is negative, the graph is concave down, and because the sign of the second derivative to the right of zero is positive, the graph is concave up.
Concave Upward: \(x=(0, \infty)\)
Concave Downward: \(x=(-\infty, 0)\)
Moreover, because the concavity changes from concave down to concave up, we also know that is a point of inflection.

How To Find Inflection Points
Cool, right?
But there’s more!
Not only can the second derivative describe concavity and identify points of inflection, but it can also help us to locate relative (local) maximums and minimums too!
Second Derivative Test Defined
Let f(x) be a function such that and the second derivative of f(x) exists on an open interval containing c.
If \(f^{\prime \prime}(c)>0\), then \(f(c)\) is a local minimum.
If \(f^{\prime \prime}(c)<0\), then \(f(c)\) is a local maximum.
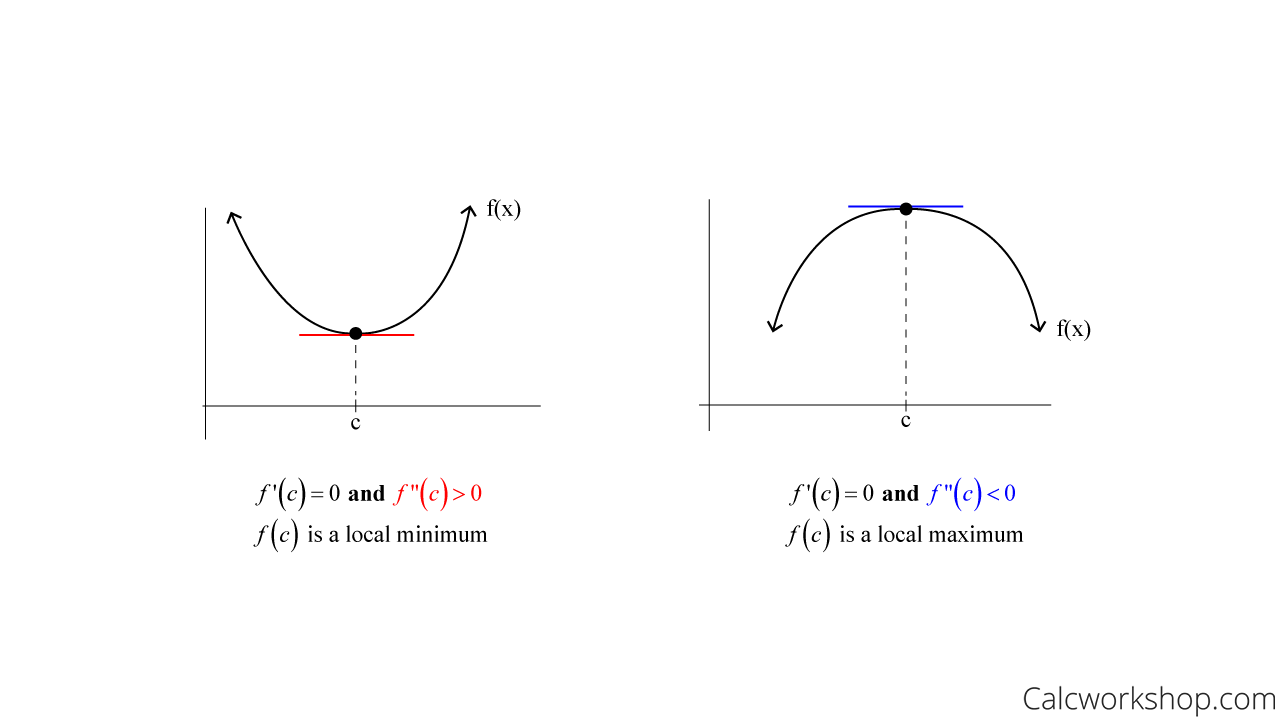
Second Derivative Test Local Extrema
And if \(f^{\prime \prime}(c)=0\), then the second derivative test fails, and in such cases, we must rely on the first derivative test only to determine relative extrema.
Okay, so let’s use this newfound skill to find relative extrema.
Use the second derivative test to find all relative extrema for \(f(x)=\frac{1}{4} x^4-\frac{2}{3} x^3-\frac{11}{2} x^2+12 x\).
We begin by finding the critical numbers of f(x) by finding the first derivative and setting it equal to zero.
\begin{equation}
\begin{aligned}
&f^{\prime}(x)=x^3-2 x^2-11 x+12 \\
&x^3-2 x^2-11 x+12=0 \\
&(x+3)(x-1)(x-4)=0 \\
&x=-3,1,4
\end{aligned}
\end{equation}
Next, we calculate the second derivative.
\begin{equation}
f^{\prime \prime}(x)=3 x^2-4 x-11
\end{equation}
Now we apply the second derivative test by substituting our critical numbers of \(x=-3,1,4\) into our second derivative to determine whether it yields a positive or negative value.
\begin{equation}
\begin{aligned}
&f^{\prime \prime}(-3)=3(-3)^2-4(-3)-11=28>0 \\
&f^{\prime \prime}(1)=3(1)^2-4(1)-11=-12<0 \\
&f^{\prime \prime}(4)=3(4)^2-4(4)-11=21>0
\end{aligned}
\end{equation}
Because the second derivative is positive (concave up) when x = -3 and when x = 4, this means that these critical numbers are both relative minimums. And because the second derivative is negative (concave down) when x = 1, this indicates that this critical number is a relative maximum.
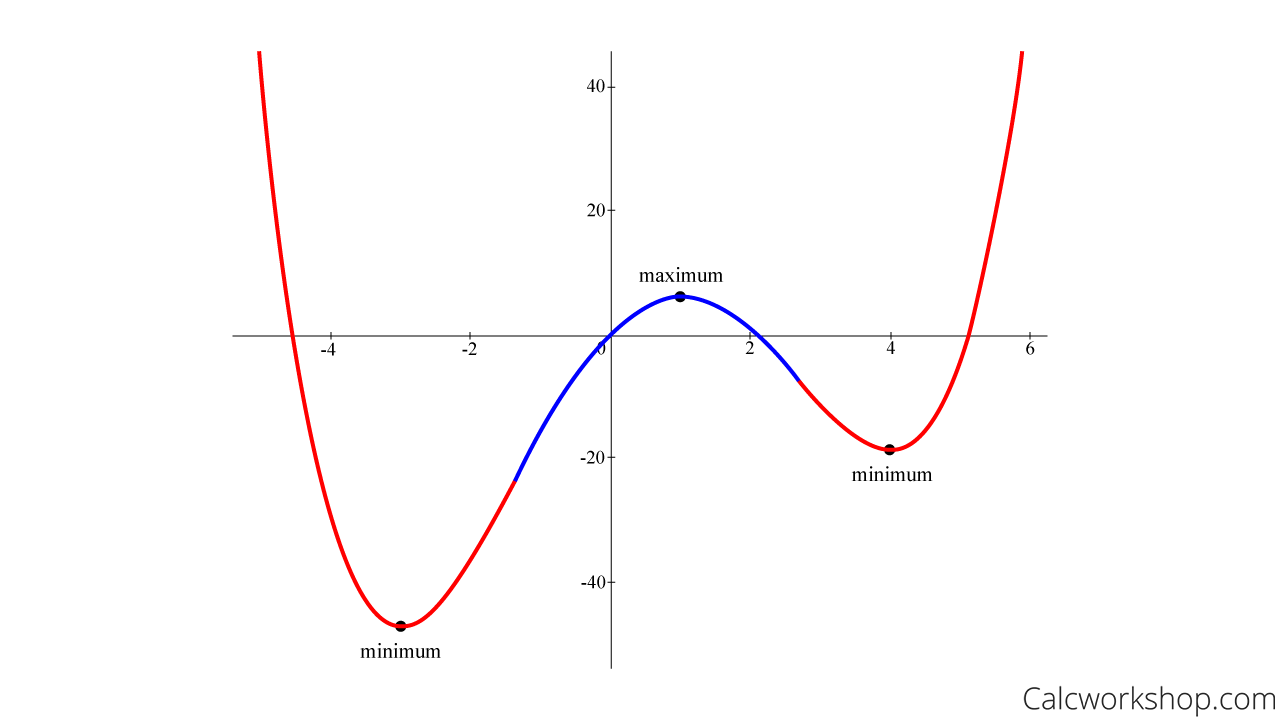
How To Find Relative Extrema Using Second Derivative Test
So, by determining where the function is concave up and concave down, we could quickly identify a local maximum and two local minimums.
Nice!
In this video lesson, we will learn how to determine the intervals of concavity (concave upward and downward), locate inflection points, and use the second derivative test to identify relative extrema.
It’s going to awesome! So, let’s get after it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.