What is the calculus formula for arc length?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Excellent question, and it’s the we’re going to cover in today’s class.
Let’s go!
What do the following scenarios all have in common?
- The distance a soccer ball takes as it soars through the air on its way to the back of the net.
- The length of a rope bridge over a raging river.
- The exact perimeter of a vase of flowers.
They all describe the distance traveled between two points along a section of a curve.
Using Steps To Approximate Curve Length
But how do find the arc length of a curve that isn’t straight?
What if I said that, if you zoom in far enough on any curve, it will always appear straight.
This means that we can apply our knowledge of the Pythagorean Theorem to find the arc curve quickly!
How?
By dividing the curve into a small number of parts, we can approximate the length by calculating the change in y and the change in x and adding up each segment.
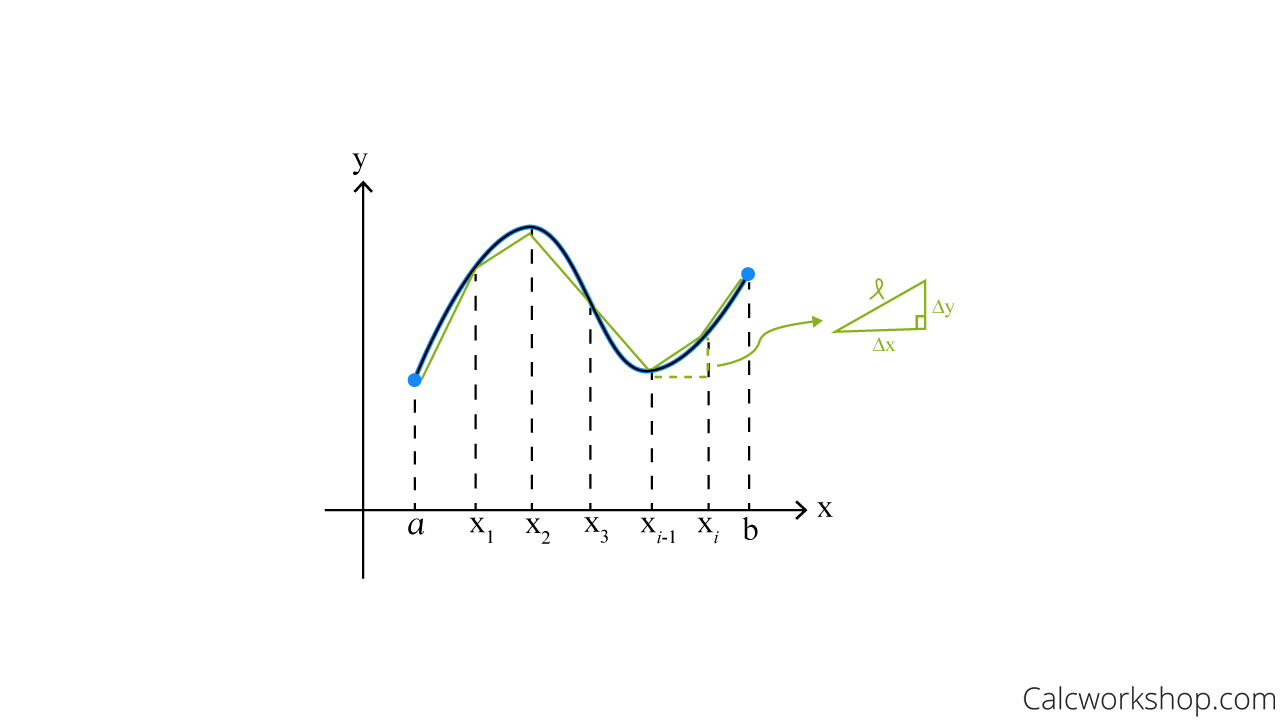
Arc Length Approximation
Isn’t it extraordinary how the method for finding the curve’s length is similar to finding the area between two curves and the volume of a solid of revolution?
We divide the curve into an infinite number of small distances, as Harvey Mudd College nicely states, and then sum their distances.
Using The Formula
Consequently, if f is a smooth curve and f’ is continuous on the closed interval [a,b], then the length of the curve is found by the following Arc Length Formula:
\begin{equation}
L=\int_{a}^{b} \sqrt{1+\left(f^{\prime}(x)\right)^{2}} d x
\end{equation}
Setup Only
Let’s see this formula in action by working on a few examples.
Suppose we are asked to set up an integral expression that will calculate the arc length of the portion of the graph between the given interval.
Example 1: \(y=5+x^{3}, 1 \leq x \leq 4\)
\begin{equation}
L=\int_{1}^{4} \sqrt{1+\underbrace{\left(3 x^{2}\right)^{2}}_{y^{\prime}(x)}} d x=\int_{1}^{4} \sqrt{1+9 x^{4}} d x
\end{equation}
Example 2: \(x=y^{5},-2 \leq y \leq 2\)
\begin{equation}
L=\int_{-2}^{2} \sqrt{1+\underbrace{\left(5 y^{4}\right)^{2}}_{x^{\prime}(y)}} d y=\int_{-2}^{2} \sqrt{1+25 y^{8}} d y
\end{equation}
See, it’s just that easy!
All we have to do is take the derivative of the function and toss it right into the formula!
Solve By Integration
Alright, so now that we know how to utilize the formula, let’s calculate the arc length using our integration skills!
\begin{equation}
\text { Find the length of the curve } y=\ln (\sec x) \text { from }\left[0, \frac{\pi}{3}\right]
\end{equation}
\begin{equation}
\text { First, we will find the derivative of the function: } \frac{d y}{d x}=\frac{\sec x \tan x}{\sec x}=\tan x
\end{equation}
Next, we substitute the derivative into our arc length formula, simplify, and integrate!
\begin{equation}
\begin{array}{l}
L=\int_{0}^{\pi / 3} \sqrt{1+(\tan x)^{2}} d x \\
L=\int_{0}^{\pi / 3} \sqrt{1+\tan ^{2} x} d x \quad \text { Pythagorean Identity } 1+\tan ^{2} x=\sec ^{2} x\\
L=\int_{0}^{\pi / 3} \sqrt{\sec ^{2} x} d x \\
L=\int_{0}^{\pi / 3}(\sec x) d x=\left.\ln (\sec x+\tan x)\right|_{0} ^{\pi / 3}=\ln \left(\sec \left(\frac{\pi}{3}\right)+\tan \left(\frac{\pi}{3}\right)\right)-\ln (\sec (0)+\tan (0)) \\
L=\ln (2+\sqrt{3})
\end{array}
\end{equation}
Not too terrible, right!
Arc Length And Surfaces Of Revolution
Okay, now let’s see how we can take our newfound knowledge of arc length and apply it to the rotation.
Did you know that a surface of revolution is formed when a curve is rotated about a line?
Imagine we have a curve, and we wish to revolve it about an axis. What would it look like?
Well, it will create a thin layer, similar to a cylinder.
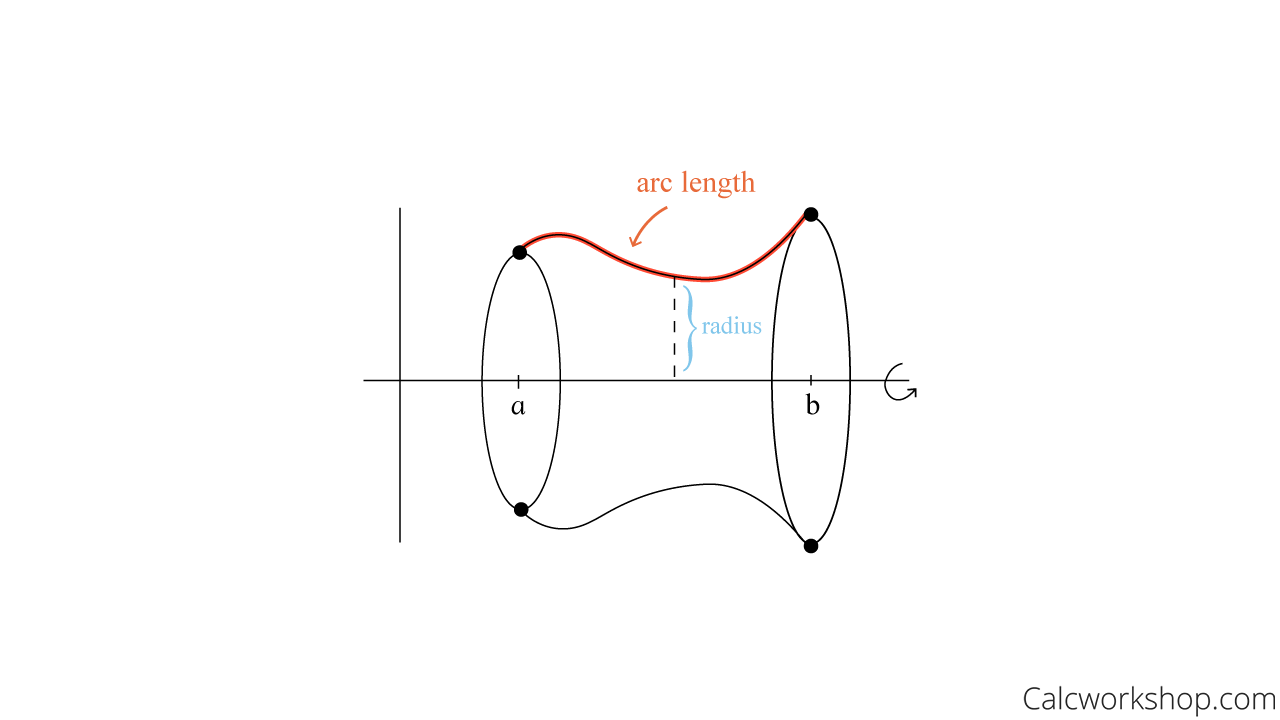
Find The Area Of The Surface Generated By Revolving The Curve
That means we can apply our knowledge of cylindrical shells and adapt it to create the area of a surface of revolution formula!
\begin{equation}
\begin{array}{l}
S A=2 \pi r l_{\Delta x}=2 \pi(\text { radius })(\text { length })(\text { thickness }) \\
S A=\int_{b}^{a} 2 \pi r(x) L(x) d x \\
S A=\int_{b}^{a} 2 \pi r(x) \sqrt{1+\left(f^{\prime}(x)\right)^{2}} d x
\end{array}
\end{equation}
Example
Let’s suppose we have the curve.
\begin{equation}
f(x)=\sqrt{4-x^{2}},-1 \leq x \leq 1
\end{equation}
And we wish to find the area of the surface obtained by rotating this arc about the x-axis.
First, we will graph our curve and identify the derivative of the function and radius.
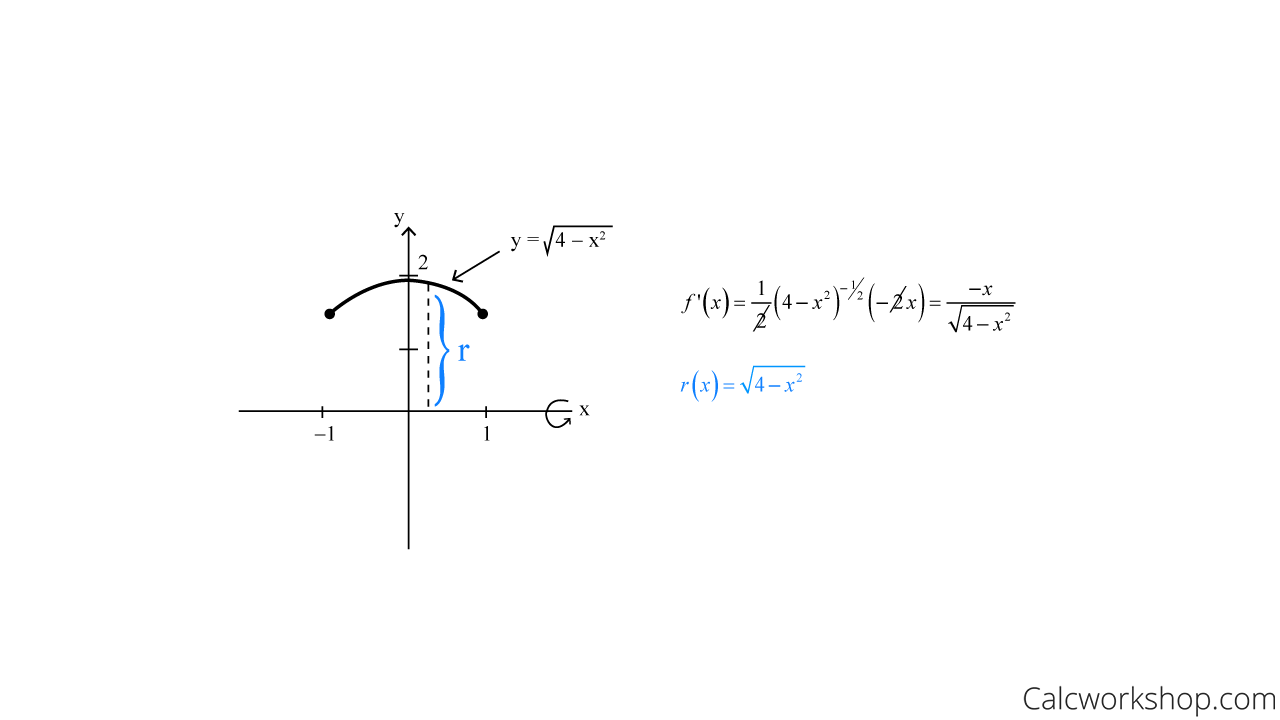
Arc Length And Surface Area Of Revolution
Next, we substitute everything into our surface area formula and integrate!
\begin{equation}
\begin{array}{l}
S A=\int_{-1}^{1} 2 \pi \underbrace{\left(\sqrt{4-x^{2}}\right)}_{\text {radius }} \underbrace{\sqrt{1+\left(\frac{-x}{\left.\sqrt{4-x^{2}}\right)^{2}}\right.}}_{\text {length }} d x \\
S A=\int_{-1}^{1} 2 \pi\left(\sqrt{4-x^{2}}\right) \sqrt{1+\left(\frac{x^{2}}{4-x^{2}}\right)} d x \\
S A=\int_{-1}^{1} 2 \pi\left(\sqrt{4-x^{2}}\right) \sqrt{\frac{\left(4-x^{2}\right)+x^{2}}{4-x^{2}}} d x \\
S A=\int_{-1}^{1} 2 \pi\left(\sqrt{4-x^{2}}\right) \frac{\sqrt{4}}{\sqrt{4-x^{2}}} d x \\
S A=\int_{-1}^{1} 4 \pi d x=\left.4 \pi x\right|_{-1} ^{1}=4 \pi(1)-4 \pi(-1) \\
S A=8 \pi
\end{array}
\end{equation}
Wow!
So we combined our knowledge of solids of revolution with arc length and calculated the surface area of an arc.
Summary
Together in this lesson, we will explore arc length and the area of a surface of revolution by developing their formulas and working through some rather challenging questions, all while applying our skills of integration.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.