Now that we understand that a set is just a collection of elements and have learned the properties involved for set operations, such as union, intersection, etc., it’s time to turn our attention to proving set identities.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
But first, we need to compile a list of all our set identities, sometimes called set properties.
Our first batch of set identities deals with subset relations, where one set is a subset of another.
The second group of properties explain the domination and complementation (negation) laws. In essence, they are rules that explain the null set and universal set as they relate to the intersection and union of a nonempty set, A.
And the third list of identities deals with equivalence, similar to those properties we used in propositional logic, such as the associative laws, distributive laws, De Morgan’s laws, etc.

Properties Subset Relations

Universal Empty Set Properties

Set Identities Discrete Math
Now let’s see how we can use our set identities to prove set theory.
There are styles of proofs for sets that we will look at:
- Venn Diagram
- Membership Table
- Proofs For Set Relations
- Proofs For Set Identities
Venn Diagram
Proofs using Venn diagrams are visual and typically quick to complete. However, there are some drawbacks. Venn diagrams are only practical for a small number of sets under consideration and are not considered robust or readily accepted in some academic circles.
Example
In this problem, we will use Venn diagrams for both the left-hand side and the right-hand side to demonstrate equivalence.
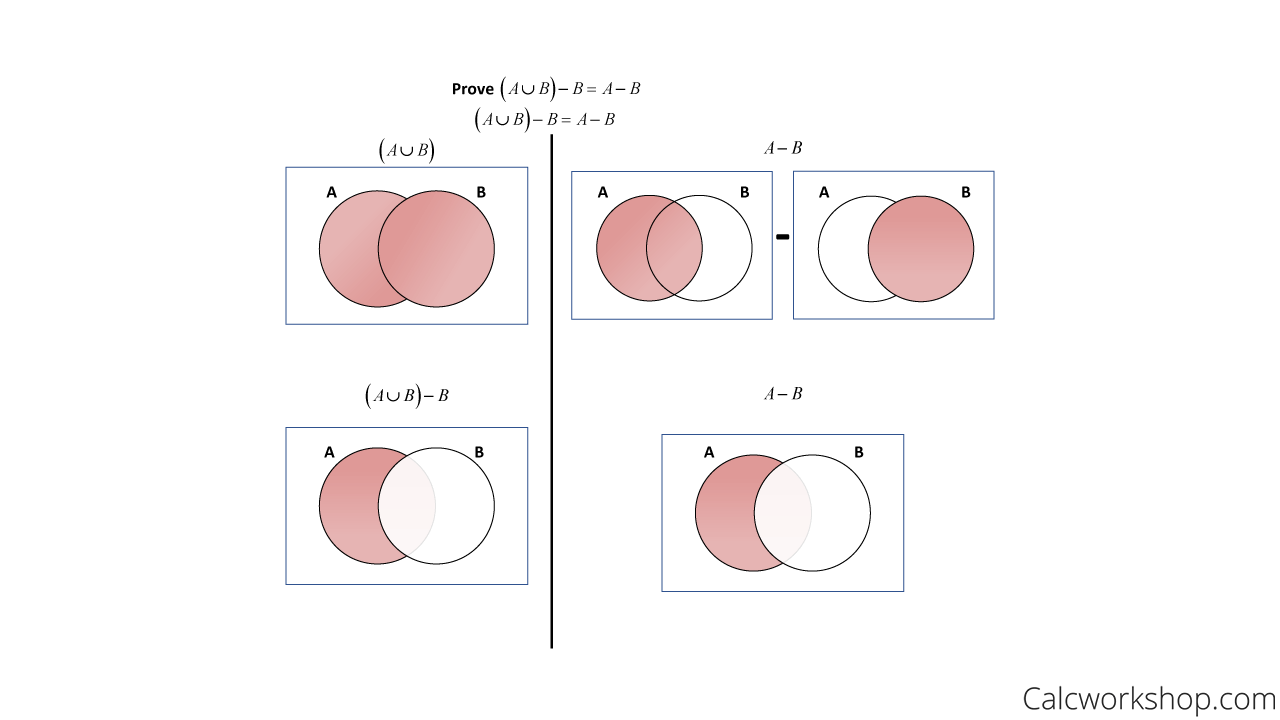
Prove Venn Diagrams Example
Membership Table
A proof by membership table is just like a proof by truth table in propositional logic, except we use 1s and 0s in place of T and F, respectively. Again, this proof style is straightforward to create, but it loses effectiveness as the number of sets increases.
Example
In this question, we will use a membership table, similar to a truth table, to verify equivalence. Notice that the red column is exactly the same as the blue column, showing the left-side is equivalent to the right side.
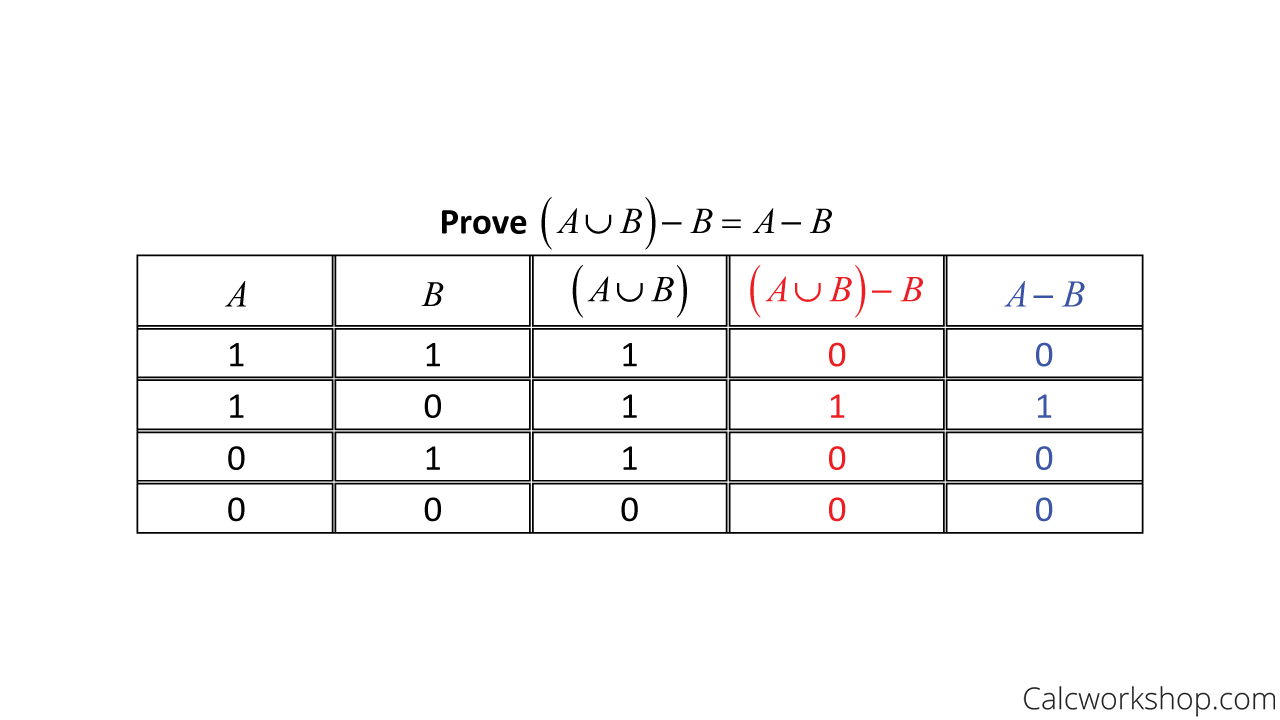
Set Membership Table
Our two remaining proof techniques involving set relation and set identities apply either direct or indirect proof methods. In fact, using either proof technique is the preferred method in set theory.
Proofs For Set Relations
When proving set relations, we wish to show that one set is a subset of another. We will use a direct proof style that involves what some textbooks refer to as the element method or the double inclusion method. The process is simple in nature as we seek to prove the left-hand side is a subset of the right-hand side or vice versa.
In other words, we want to show that a given object is an element of the set.
Example
In this problem, let’s prove the transitive property of subsets. Suppose A is a subset of B and B is a subset of C, show that A is a subset of C.

Verify Subset Transitivity Example
Proofs For Set Identities
And for proving set identities, we will utilize a style that is sometimes called proof by definition. For these types of proofs, we will again employ all of our proof strategies like direct, indirect (contraposition and contradiction), and cases along with our set identities and definitions and either write our proof in paragraph form or as a two-column proof with justifications.
Example

Prove Set Identities Example
Doesn’t this remind you of how we prove propositional logic?
Yes, the similarities are striking!
So, together we will walk through numerous examples of how to prove sets using various techniques while emphasizing and reinforcing our definition and set properties.
Let’s get to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)
1 hr 39 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.