Did you know that the term graph in mathematics can refer to a group of connected objects?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In fact, there are two types of graphs of importance in discrete mathematics:
- Directed Graphs.
- Undirected Graphs.
Directed Vs Undirected Graph
Now, we’ve already seen directed graphs when we studied relations, but let’s quickly review the main points here:
A directed graph, or digraph, is when the edges in a graph have arrows indicating direction, as illustrated below.
Similarly, an undirected graph occurs when the edges in a graph are bidirectional, meaning they represent motion in both directions (i.e., a to b and b to a). And some undirected graphs are called networks.
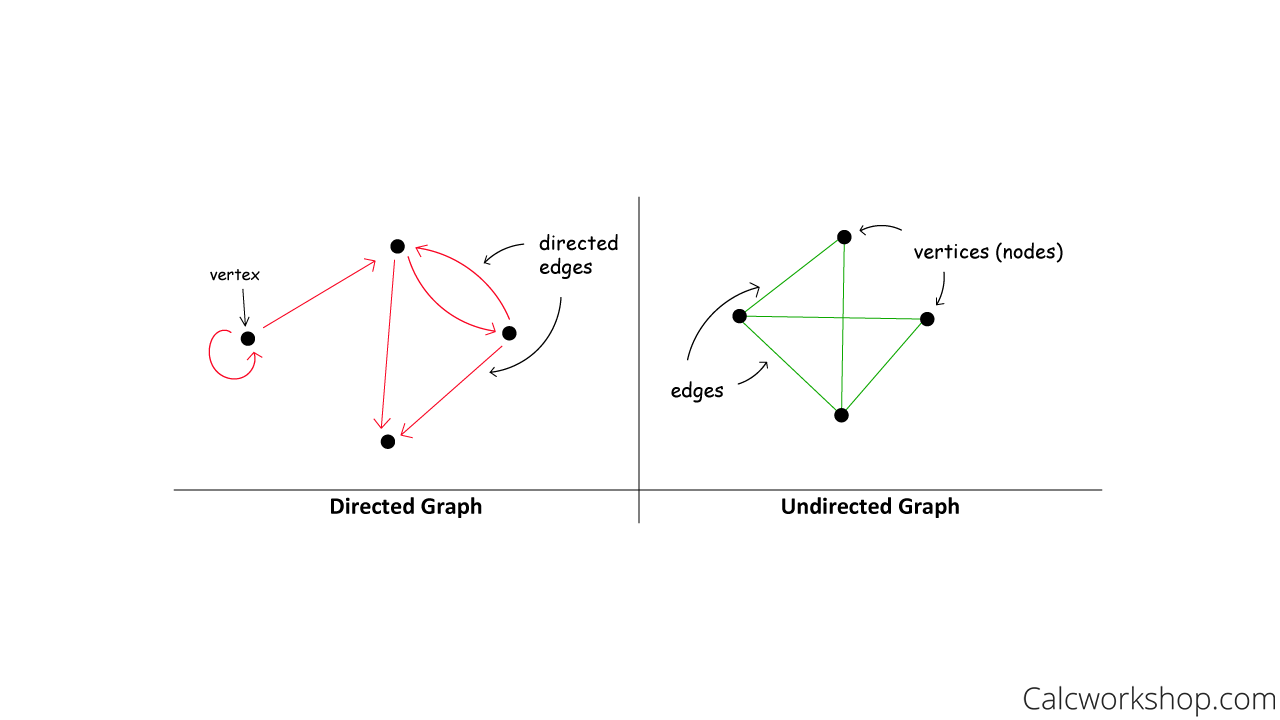
Directed Vs Undirected Graph
Formally, a graph G = (V, E) consists of a set of vertices or nodes (V) and a set of edges (E). Each edge has either one or two vertices associated with, called endpoints, and an edge is said to connect its endpoints.
And there are special types of graphs common in the study of graph theory:
- Simple Graphs
- Multigraphs
- Pseudographs
- Mixed Graphs
Their properties are illustrated in the following table.
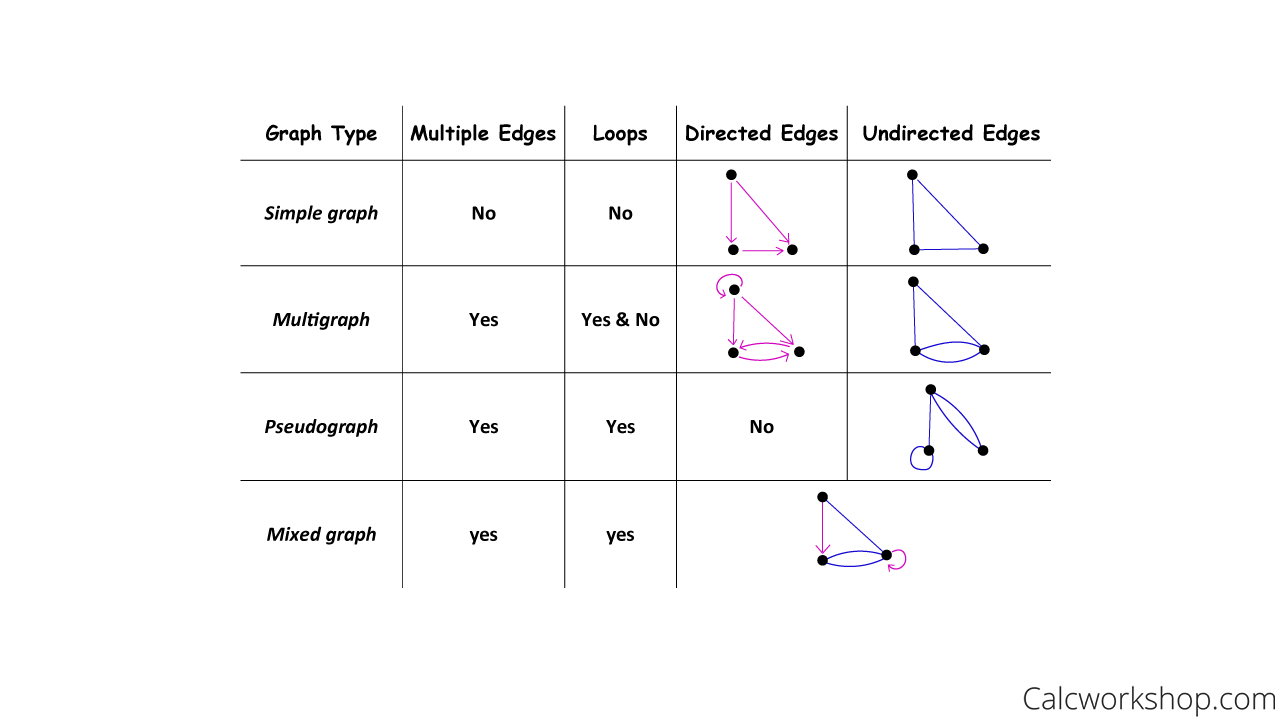
Graph Type: Simple, Multi, Pseudo, Mixed
Vertices are called adjacent or neighbors, denoted N(V) if they are endpoints of the same edge. Such an edge is called incident with the vertices, or more simply, the edge connects the two vertices as noted by Whitman College.
Additionally, the degree of a vertex in an undirected graph is the number of edges incident with it and where all loops are counted twice. A vertex with a degree of zero is considered isolated, and a vertex of degree 1 is regarded as a pendant.
Example
Using the undirected graph below, let’s identify the degree and neighborhood for each vertex.

Identify Degree and Adjacent Vertices
Handshake Theorem
And this now leads us to a fundamental idea called the Handshake Theorem, which states that the sum of the degrees of the vertices of an undirected graph is equal to twice the number of edges.

Handshake Theorem In Discrete Mathematics
Examples
Let’s look at an example of this in action.
Suppose there are 9 people in a room, and they all shake hands with everyone else. This means that each person will shake hands with 8 other people (you wouldn’t shake hands with yourself because that would be strange).
Anyway, that means that each vertex (person) has a degree of 8, and if we add up all of these degrees, we get:
- 8+8+8+8+8+8+8+8+8 = 72
If we apply the handshake theorem, this means:
- 2m = 72 or m = 36 handshakes (edges)
Key Point: There’s a hidden implication within the handshake theorem, as we can also determine if a particular combination of handshakes (edges) is impossible.
For example, suppose we asked these same 9 people only to shake hands with exactly 5 people.
This suggests that the degree of each vertex (person) is 5, giving a sum of:
- 5+5+5+5+5+5+5+5+5 = 45
But after applying the handshake theorem:
- 2m = 45 yields an answer of 22.5
Which is impossible as we can’t have “half” of a handshake or edge.
Walk Trails Paths
Okay, so now let’s talk about some cool attributes that are special so some types of graphs.
In discrete mathematics, a walk is a finite path that joins a sequence of vertices where vertices and edges can be repeated. In other words, every time you “traverse” a graph, you get a walk.
Now a trail is a walk in which all the edges are distinct, but a vertex can be repeated.
Next a path is a trail that joins a sequence of vertices and distinct edges where no vertex nor edge is repeated, and vertices are listed in order.
And a graph is said to be connected if every pair of vertices in the graph is linked. This means that there is a path between every pair of vertices.
The graphs below nicely highlight the differences between a walk, trail, and path.

Identify Walk, Trails, and Paths
Completed Graphs
Moreover, suppose a graph is simple, and every vertex is connected to every other vertex. In that case, it is called a completed graph, denoted K. In fact, completed graphs are sometimes considered regular. Below are a few examples of completed graphs.

Complete Graph Example
Cycles And Circuits
A cycle denoted C is a path that begins and ends at the same vertex, whereas a circuit is a closed trail, meaning no edges are repeated, but just like a cycle, you start and stop and the same place. In fact, cycles are also circuits. Below are some examples of cycles and circuits.

Cycle Vs Circuit Graph Theory
Wheels
And a wheel denoted W is obtained by adding an additional vertex to a cycle. In other words, it looks like spokes on a wheel. The graphs below are a few examples of wheels.

Wheel Graph Example
Bipartite Graphs
Now it’s time to talk about bipartite graphs.
A bipartite graph is when the set of vertices can be partitioned into two disjoint subsets such that each edge connects a vertex from one subset to a vertex of the other.
To determine whether a graph is bipartite, we use a coloring system. A simple graph is bipartite if and only if it is possible to assign one of two colors to each vertex so that no two adjacent vertices are the same color.
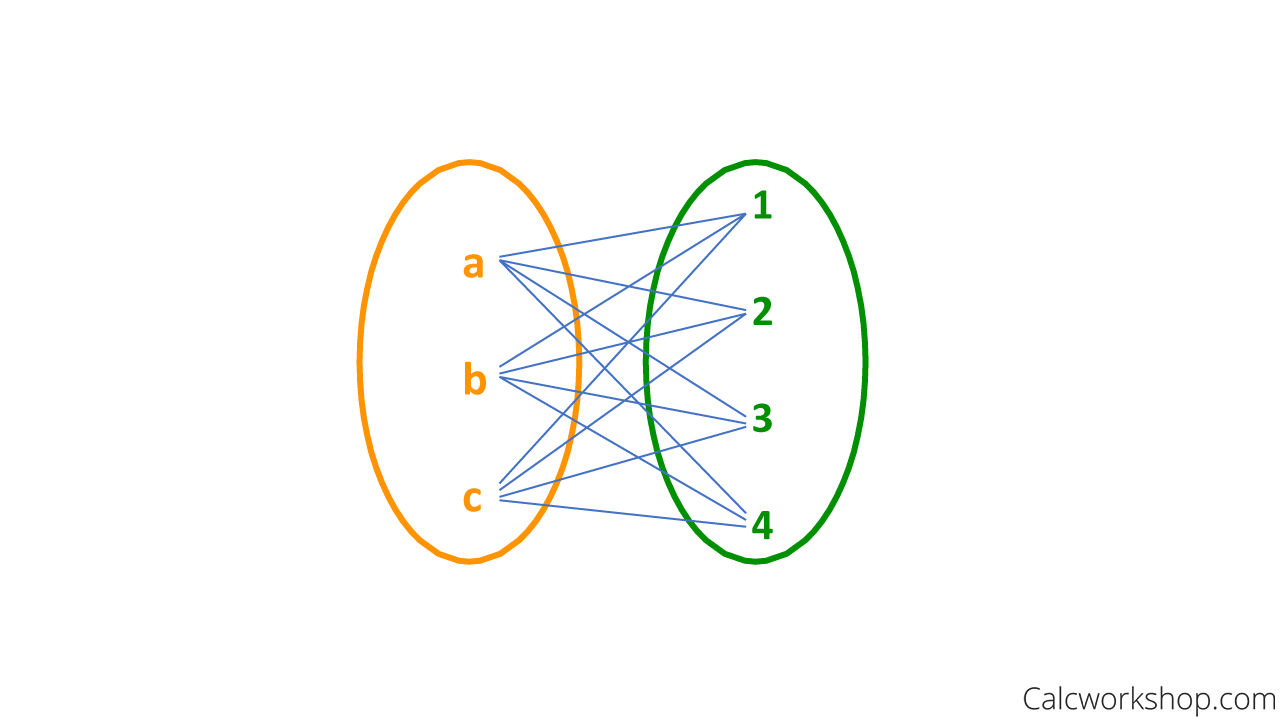
Bipartite Set Example
How To Tell If A Graph Is Bipartite
- Pick two colors (i.e., orange and green)
- Choose a vertex to start at and color that vertex Orange.
- Color all the adjacent vertices Green (all vertices that are in the neighborhood of your first orange vertex).
- Now color all the adjacent neighbors of the Green vertices Orange and continue this pattern until all vertices are colored.
If every adjacent vertex is a different color, then the graph is bipartite. Otherwise, not bipartite.
Example
For example, in the graph below on the left, every vertex alternates orange then green. However, the graph on the right shows green vertices adjacent (connected); thus, the right graph is not bipartite.
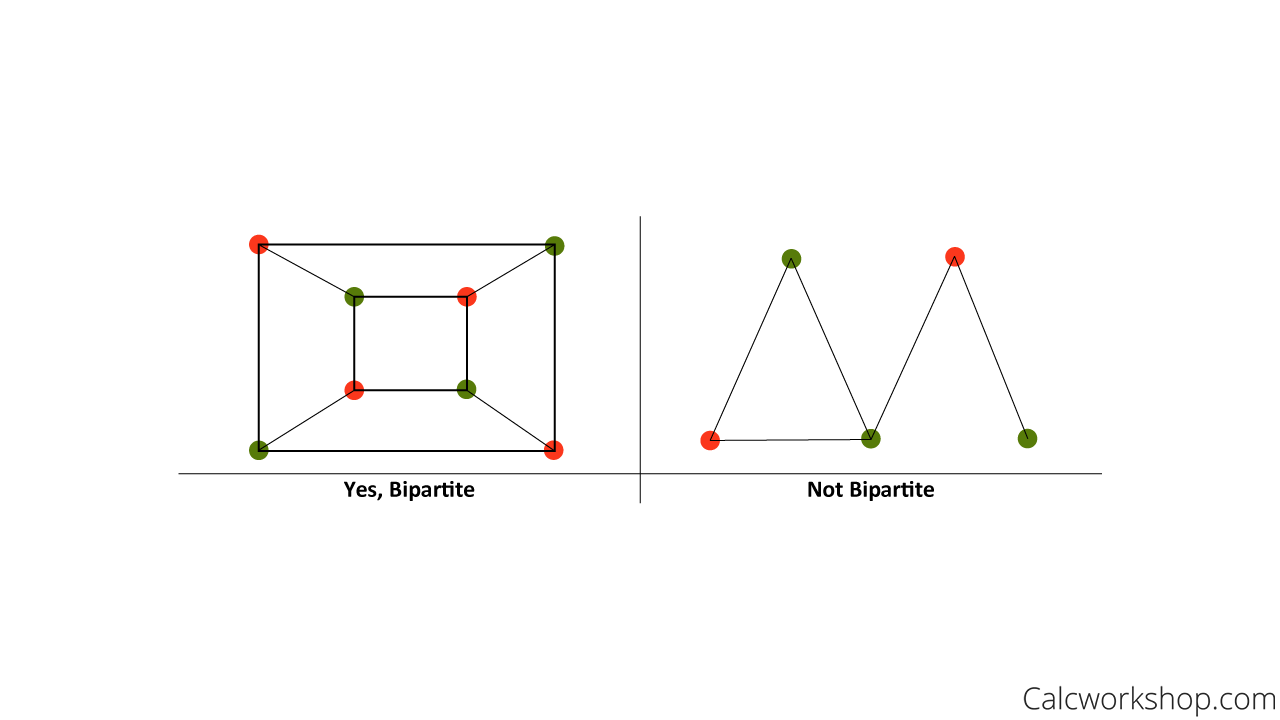
Bipartite Color Technique
Summary and Path Forward
In this video lesson, we will learn how to identify the types of graphs, degrees, and neighborhoods. As well as special simple graphs such as walks, trails, paths, circuits, cycles, wheels, and connected graphs. Additionally, we will successfully apply the handshake theorem to determine the number of edges and vertices of a graph, learn how to create subgraphs and unions of graphs, and determine if a graph is bipartite.
There’s a lot to explore, so let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.