Did you know that a function is also called a transformation or mapping?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
The notion of functions is not new to us, as we studied them in high school algebra and precalculus, but in discrete mathematics we want to take that understanding and adapt it to set theory.
What Is A Function
A function, f, from set A to set B, is a rule that assigns each element of A to exactly one element in B, and we write f(a)=b and say f maps a to b.
To indicate that f is a function from A to B we write:

Function Notation
Characteristics Of Functions
Additionally, a function is not complete unless we specify its domain, codomain, range, and rule. So, let’s look at a few definitions that will be extremely important to us:
- Relation: Set of ordered pairs.
- Domain: Set A on which f is defined. It represents the set of inputs or first elements and is called the preimage.
- Codomain: Set B in which f takes its values. It represents the set of possible outputs or second elements.
- Range: While the codomain is the set of possible outcomes, the range is the set of actual outcomes, and is called the image.
The range is a subset of the codomain of f, as the arrow diagram below nicely illustrates.
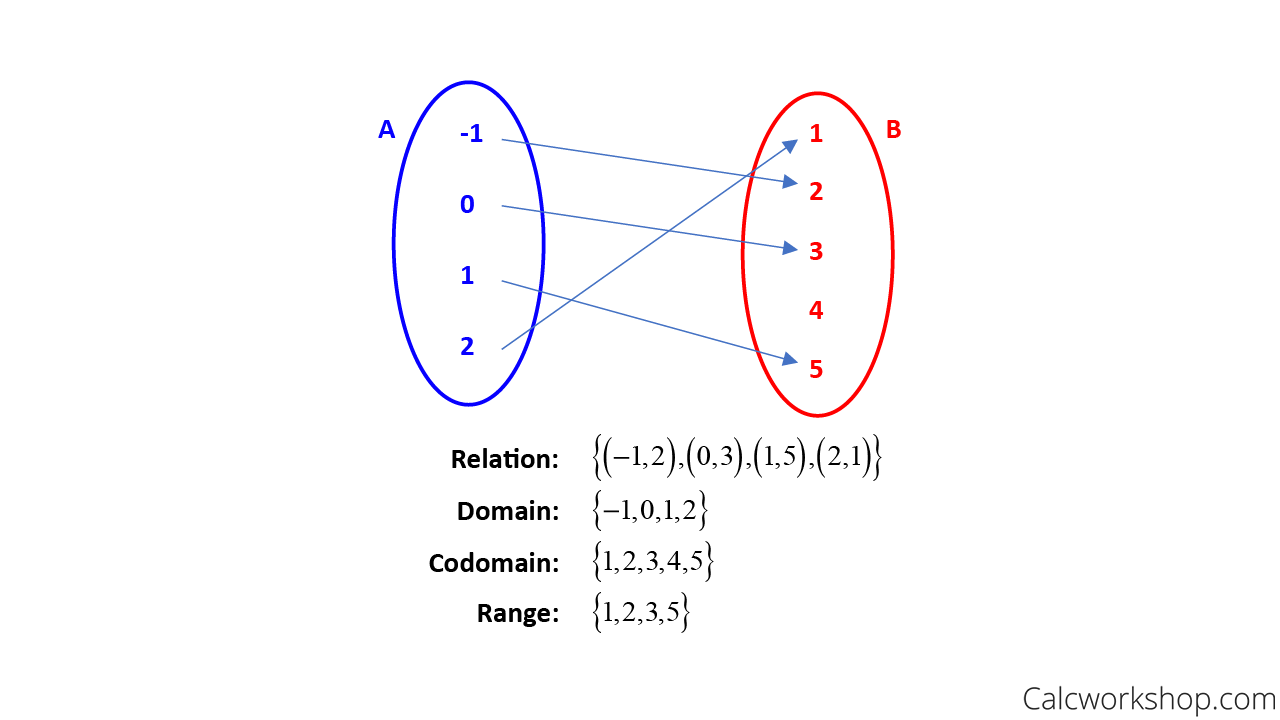
Domain Codomain Range Relation — Example
Notice that the codomain represents all the possible y-values, and the range indicates all the “actual” y-values.
Real Vs Integer Valued Functions
Seeing as in algebra and precalculus we only dealt with functions whose domains and ranges were contained in the Real Numbers the range and codomain were synonymous, and that is why most instructors only used the phrase “range” when discussing output values. Such functions are called real-valued functions, as its codomain is the set of real numbers.
But for discrete mathematics we will be looking at functions in terms of mappings of sets whose elements may be contained in the integers, not real numbers, these functions are called integer-valued as their codomain is the set of integers.
But thankfully, regardless of the number system we are working in, what you learned back in precalculus is still true for discrete mathematics — a function is a special type of relation where each x-value is unique, therefore we can and will still apply the vertical line test!
The Vertical Line Test says that if you draw a vertical line through a graph and it intersects the graph only once, then the graph is a function. For example, let’s look at the line y = –x and determine if it is a function, as well as identify the domain, codomain, and range.
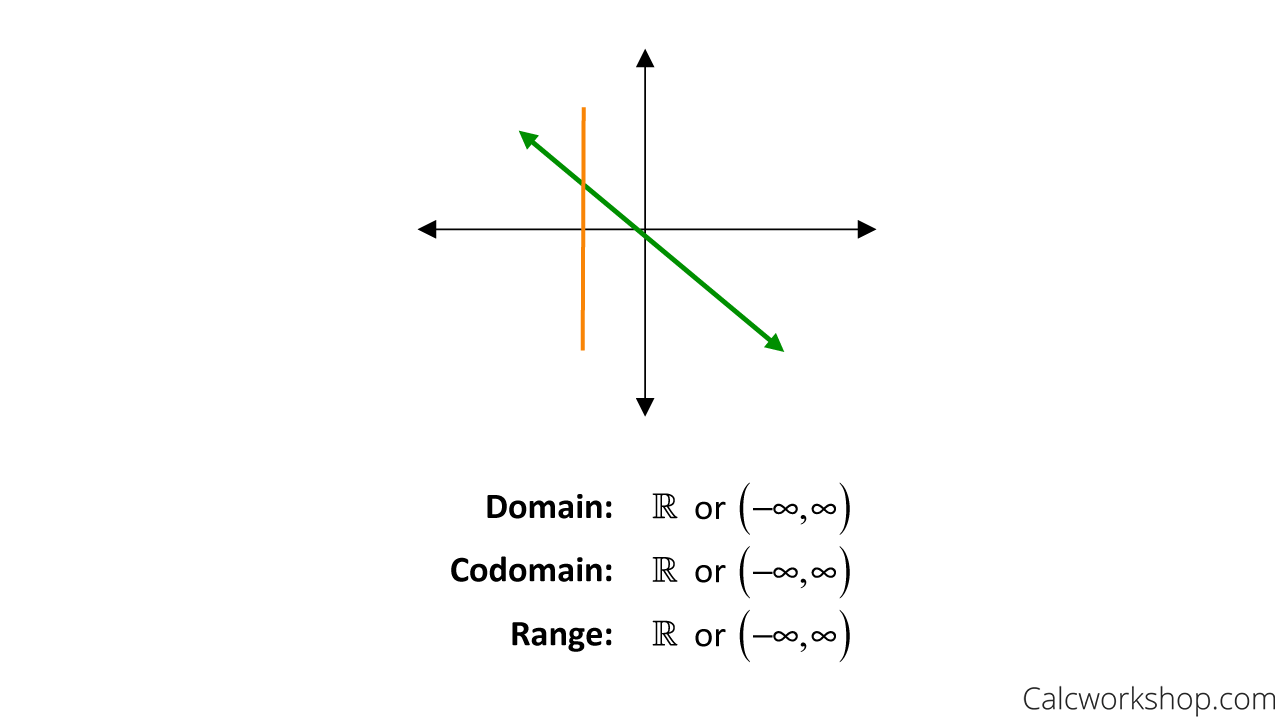
Vertical Line Test Function
Types Of Functions
Now, there are some special types of functions and operations that we want to highlight as they are vital to understanding functions on sets.
Identity Function
In other words, the identity function assigns each element to itself and is denoted:

Identity Function Definition
Binary Relation
A functional relation is a binary relation between sets A and B. For example, suppose set A = {a,b,c} and set B = {1,2,3,4} then the relation, R, from A to B is a subset of the Cartesian product A x B. Thus, if we could possibly say R = {(a,1),(b,2),(c,4)}.

Binary Relation Definition
Sum And Product Functions
Now sum and product functions are combinations of two or more functions under the operators of addition and multiplication.
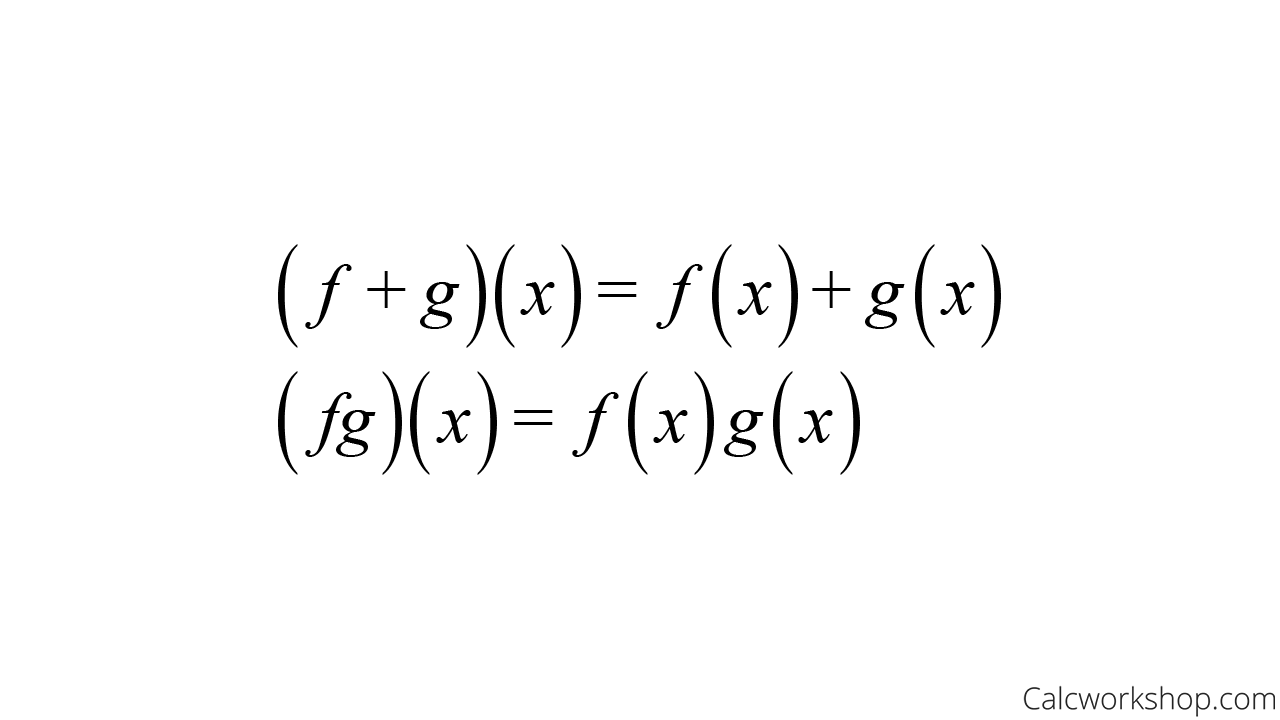
Sum Product Function Definition
For example, assume:
\begin{equation}
f(x)=7-2 x
\end{equation}
\begin{equation}
g(x)=(5 x+1)
\end{equation}
Where both f and g are defined from the real numbers, let’s find (f+g) and (fg).
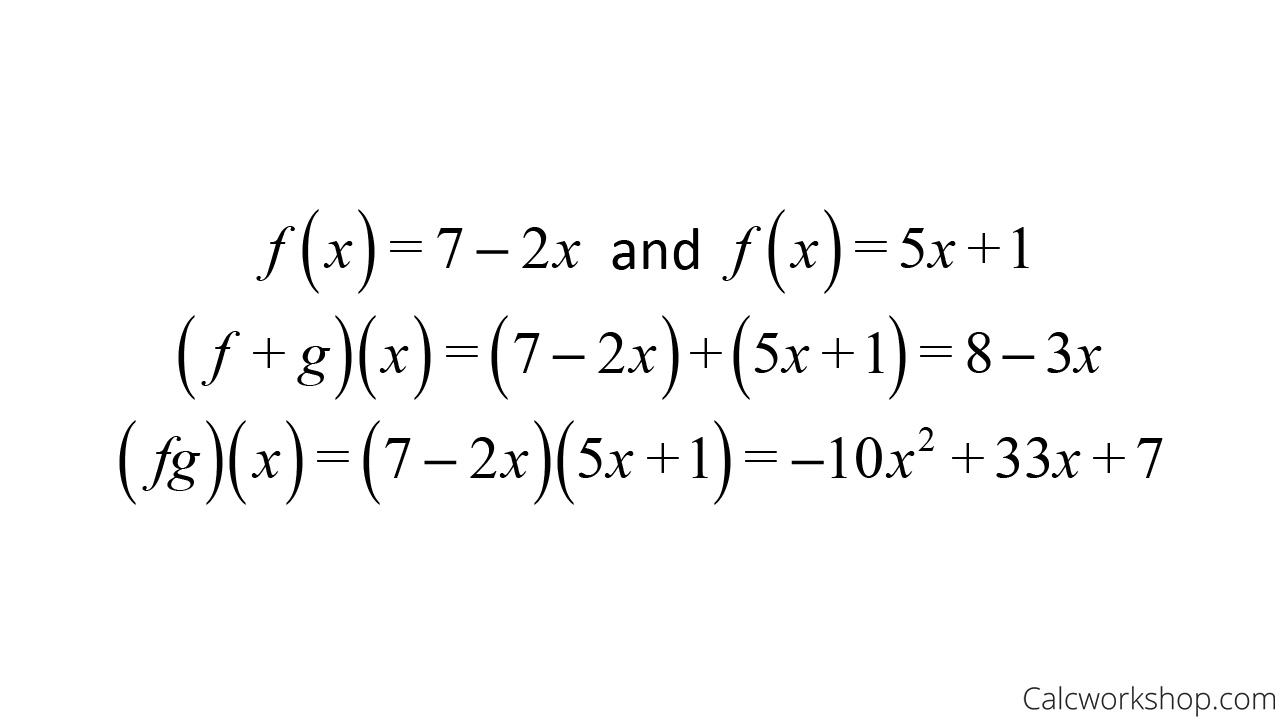
Operations Functions — Example
Composite Function
Likewise, we have the composite function that says if f and g are functions, then the composition of g and f is g(f(x)) for all x in the domain of f such that f(x) is in the domain of g. But this definition is a bit limited as it applies to real-valued functions only.
How can we adapt this to sets?
Using our example from above, assume:
\begin{equation}
f(x)=7-2 x
\end{equation}
\begin{equation}
g(x)=(5 x+1)
\end{equation}
Then
\begin{equation}
g(f(x))=5(7-2 x)+1=35+10 x+1=36-10 x
\end{equation}
Let A, B, and C be sets and suppose f is a function that maps A to B and g is a function that maps B to C, then composition of g and f is the function A to C defined by

Composite Functions Definition
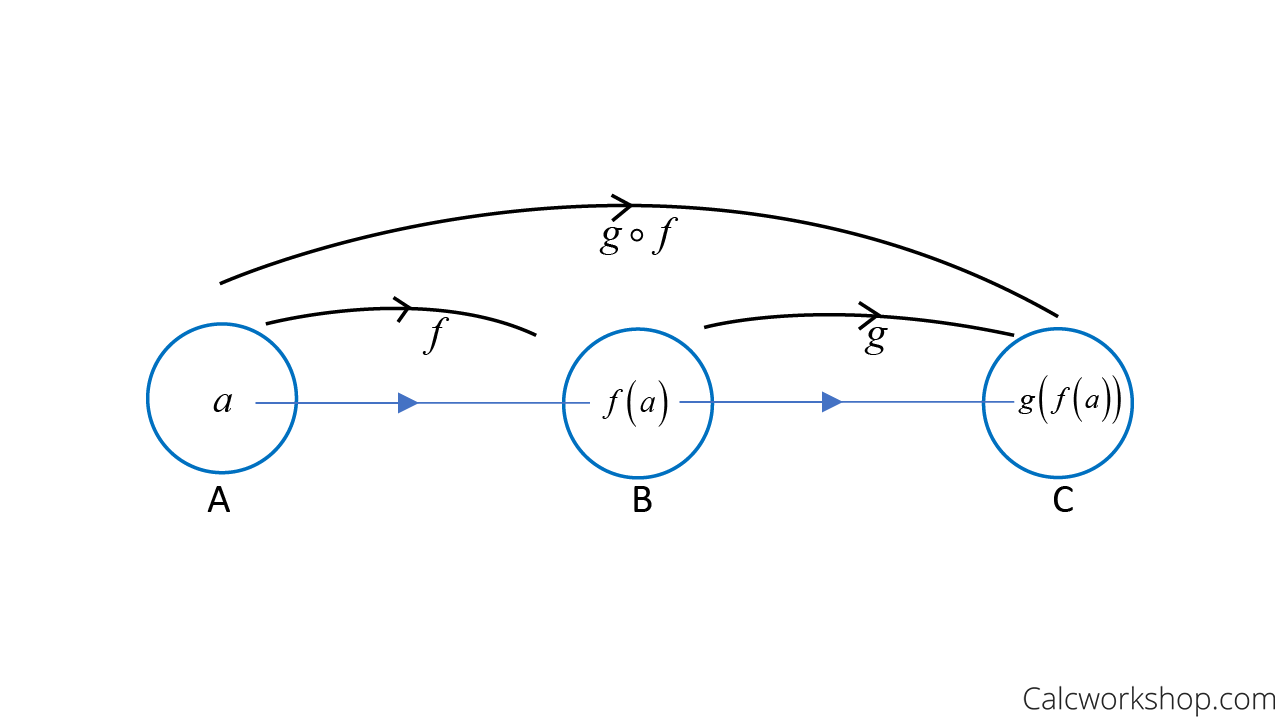
Composite Function Sets Diagram
Let’s look at an example.
Suppose
\begin{equation}
\begin{array}{l}
A=\{a, b, c\} \\
B=\{1,2,3,4\} \\
C=\{x, y, z\}
\end{array}
\end{equation}
Find the composite function of g(f(x)) if f is a function that maps A to B and g is a function that maps B to C such that:
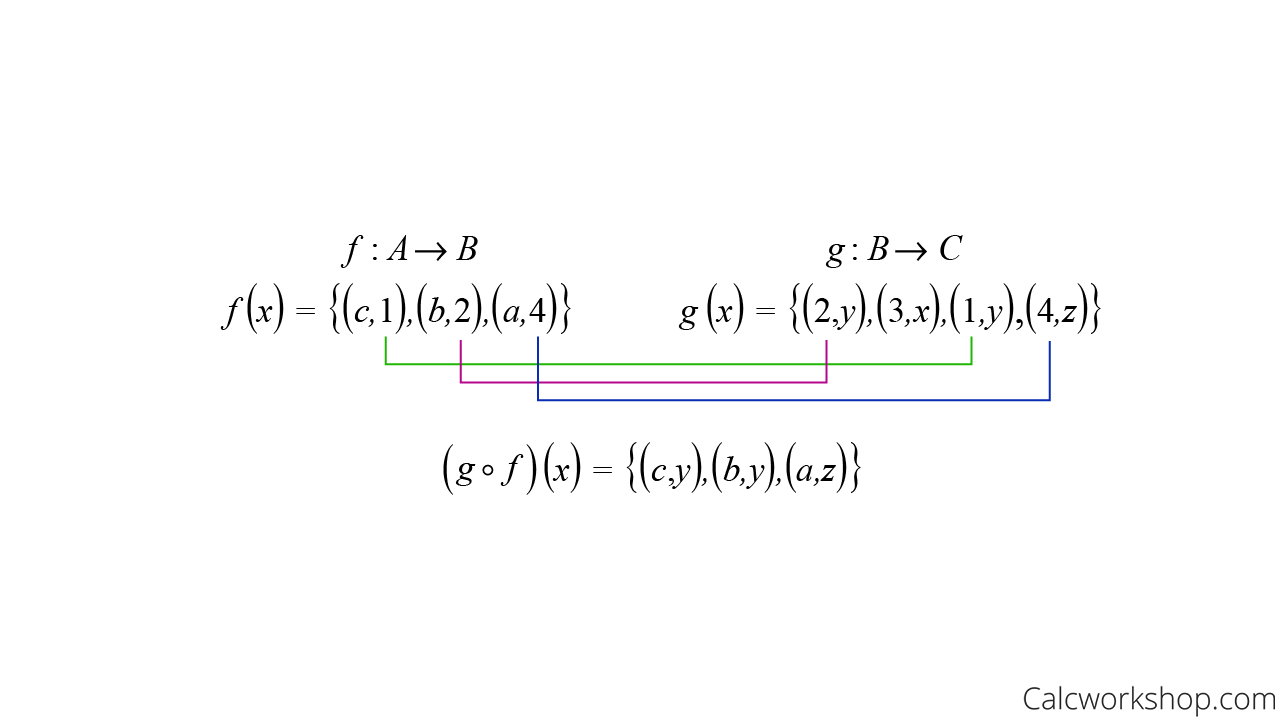
Composite Function Sets — Example
Notice that all we did was match the second elements of function f with the first elements of the function g to find our composite function. And here’s a big hint… we will use this process again when we combine relations to find composition and powers of relations in a future lesson!
Floor And Ceiling Functions
Lastly, we need to discuss two extremely useful functions called the Floor Function and Ceiling Function.
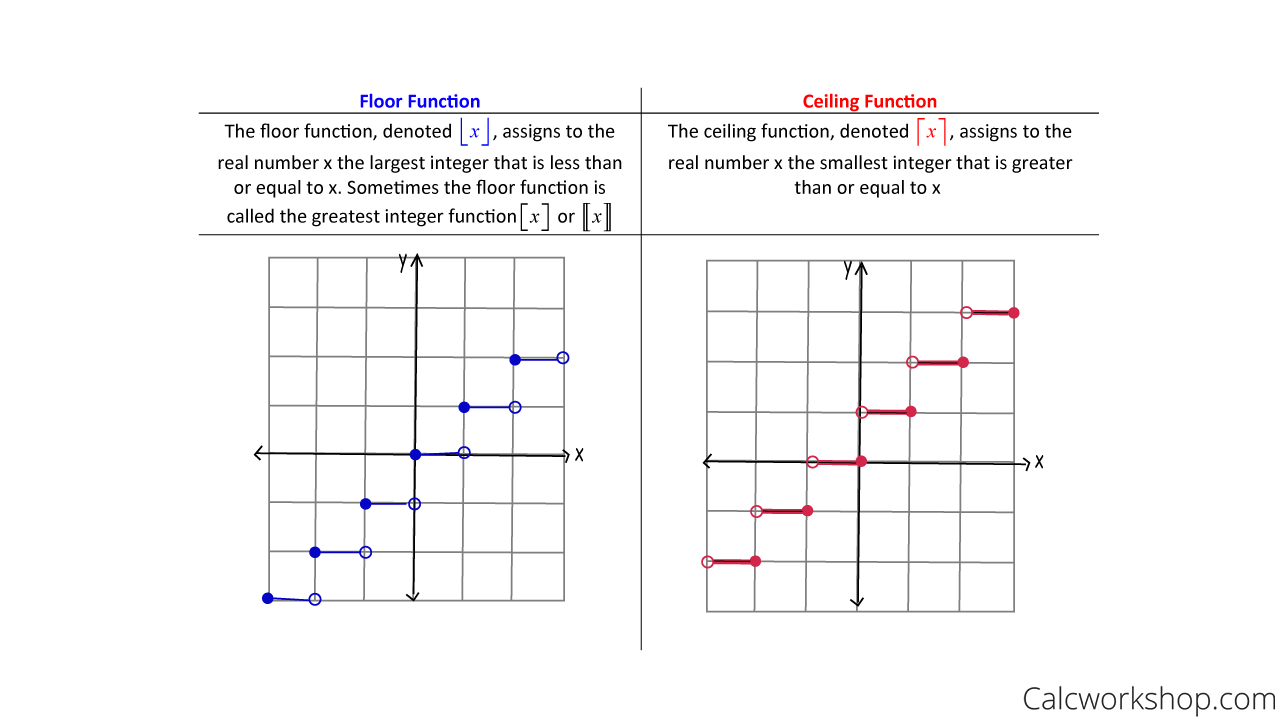
Floor And Ceiling Functions
What does this really mean?
The floor of a real number x, is the largest integer that is no larger than x, whereas the ceiling of a real number x, is the smallest integer no smaller than x.
So, suppose we are given the real number 5.6. The floor of 5.6 is 5 because it is the largest integer that isn’t larger than 5.6. And the ceiling of 5.6 is 6 because it’s the smallest integer that isn’t smaller than 5.6
Hmmm, that means on a number line, the floor assumes the integers to the left of x and the ceiling takes on the value of the integers to the right of x. And if x just so happens to be an integer already, then the floor and ceiling will just be x itself!
Alright, so let’s practice this idea with a few problems.

Evaluate Using Floor Ceiling
Not too difficult, right?
Okay, so together we will review our vocabulary and understanding of mapping, learn how to specify the domain, codomain, range, and rule for functions, as well as how to perform special function operations such as sum, product and composition. Additionally, we will explore the ceiling and floor functions as they will enable us to perform counting calculations in future combinatorics lessons.
Let’s jump to it!
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 4 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.