What does a divides b mean?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Great question!
And it’s exactly what you’re going to learn in today’s discrete lesson.
Let’s jump in!
Notation
One of the most important concepts in discrete mathematics and the study of number theory is the notion of divisibility.
Likewise, if an integer a does not divide evenly into a second integer b, then we say that “a does not divide b”

A Divides B Notation
This is to say that a is a factor or divisor of b, and that b is a multiple of a.

A Divides B Definition
Example
For example, let’s determine whether 5 | 15 and whether 5 | 21.

Does A Divide B — Example
As we can see, 5 divides 15 seeing as 15 is a multiple of 5. But 5 does not divide 21 evenly as 21/5 is not a positive integer.
Divisibility Of Integers And Their Properties
And just like we would expect, there are some basic properties of divisibility of integers. If a b and c are integers and a does not equal zero, then:
- If a|b and a|c, then a|(b + c)
- If a|b, then a|bc
- If a|b and b|c, then a|c
- If a|b and a|c, then a|(mb + nc) whenever m and n are integers
Together we will prove each of these properties in our lesson, but for now let see how these rules help to develop the division algorithm.
What Is The Division Algorithm
The Division Algorithm states that if we let a be an integer and d a positive integer, then there are unique integers q and r, such that if d divides a then
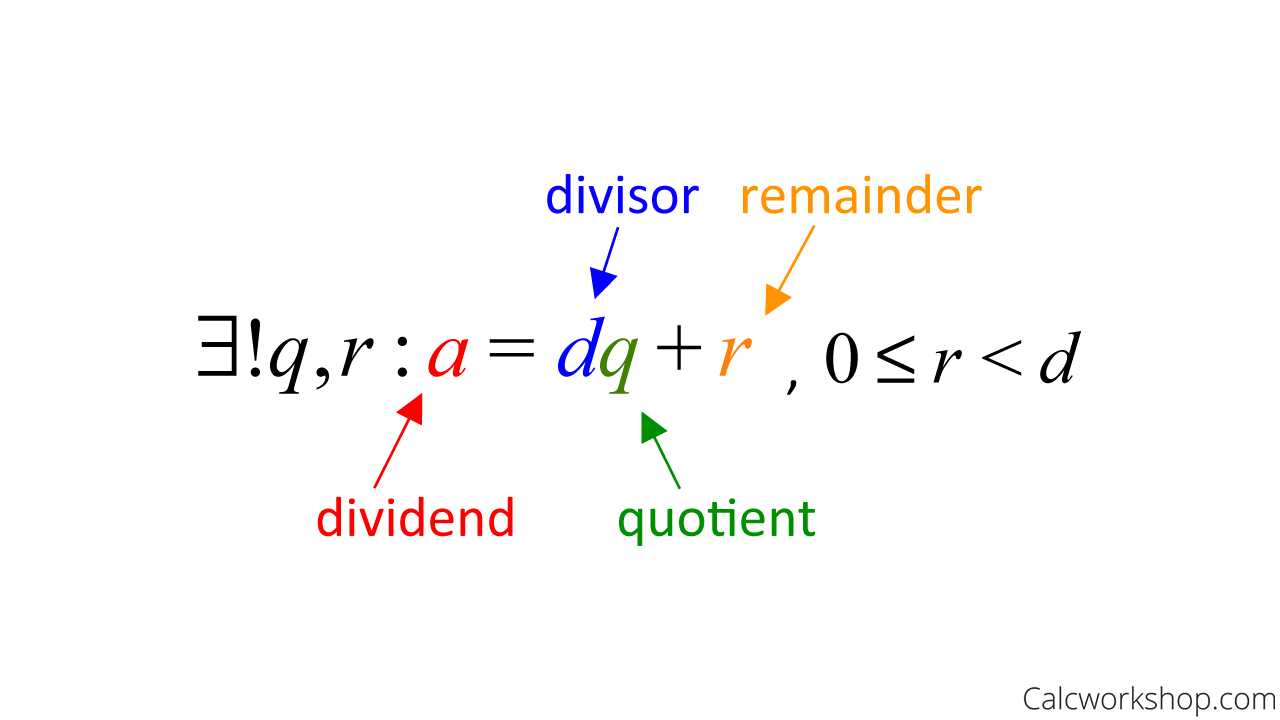
Division Algorithm — Discrete Math
In the above stated algorithm, a is the dividend, d is the divisor, q is the quotient and r is the remainder as noted by the University of Victoria.
Note that modulo, or modulus or mod, is the remainder after dividing a by d.
We will be studying modulo operations in great depth in our next lesson, but for now we will learn the basics of how to write our remainder using mod operators.
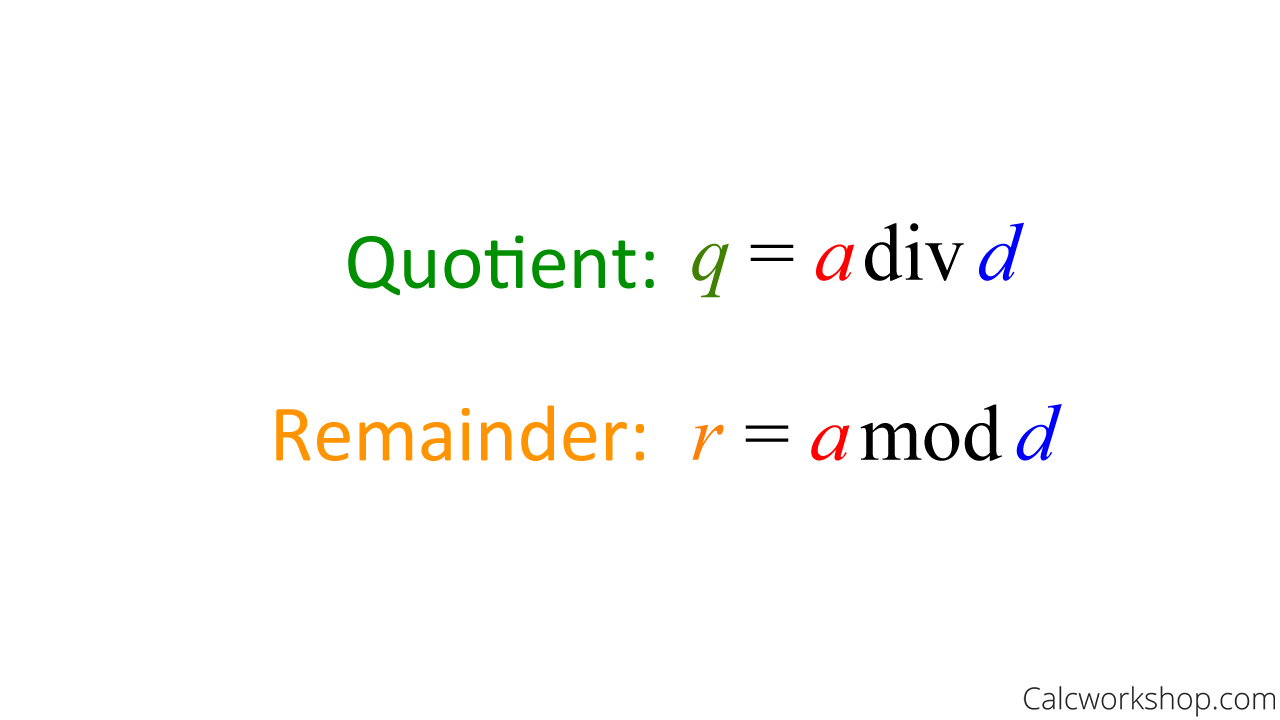
Discrete Math Quotient Remainder Theorem
Example
For example, what are the quotient and remainder when 19 is divided by 7?

Find Quotient Remainder — Example
Throughout this lesson we will verify the basic properties of divisibility and learn how to express the quotient and remainder following the division algorithm.
Let’s jump right in.
Video Tutorial w/ Full Lesson & Detailed Examples
57 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.