Did you know that one of the most fundamental concepts in mathematics is a set?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Set Definition
A set is a collection of well-defined, unordered objects called elements or members. All this means is that it is clear which pieces belong in the set, and their order in the set isn’t important.
For example, let’s say we have a bowl of fruit on the table, and inside the bowl, there is an apple, orange, pear, and banana.

Set Analogy – Fruit Bowl
The bowl represents the set, as it contains the fruit. And each fruit represents the elements or members of the group. Now, I want you to notice that it doesn’t matter which order we list the members, as we can say {apple, orange, pear, banana} just as easily as we can say {orange, banana, apple, pear}. But what is essential is that we can see that these four fruits belong in this particular set.
Set Notation
It is common to use braces, or as I like to call them, wiggle or curly brackets, to enclose a set. Additionally, we use capital letters to represent or name a set. Notice how we used “B” for the bowl in our example above.
Types Of Sets
Moreover, there are three ways we can describe a set mathematically:
- Roster Method
- Words
- Set-Builder Notation
The roster method lists all the elements or members in the set, whereas a description in words explains what elements are in the set using a sentence. And set-builder notation expresses how elements are given membership in the set by specifying the properties that define the collection of objects.
For example, suppose we wish to describe the set A = {1, 2, …, 5}.

Roster Method Vs Set Builder Notation
Equal Vs Unequal Sets
Now, if two sets contain precisely the same elements, regardless of the order or possible repetition, then they are considered equal.
Suppose set A = {1,3,5} and set B = {5,5,3,3,1,1}. Sets A and B are equal because they contain the exact same elements, namely 1, 3, and 5. Remember, order and multiplicity of elements don’t matter.
Let’s look at another example. Determine if the sets A and B are equal
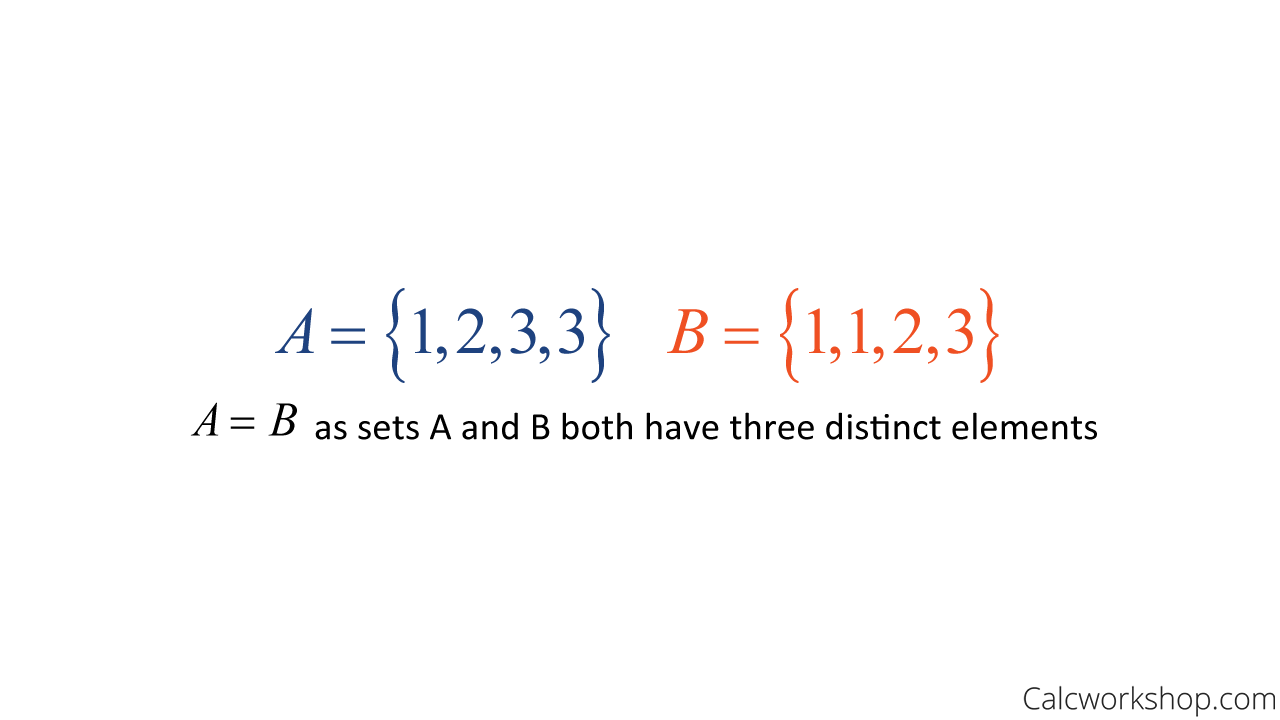
Equal Sets Example
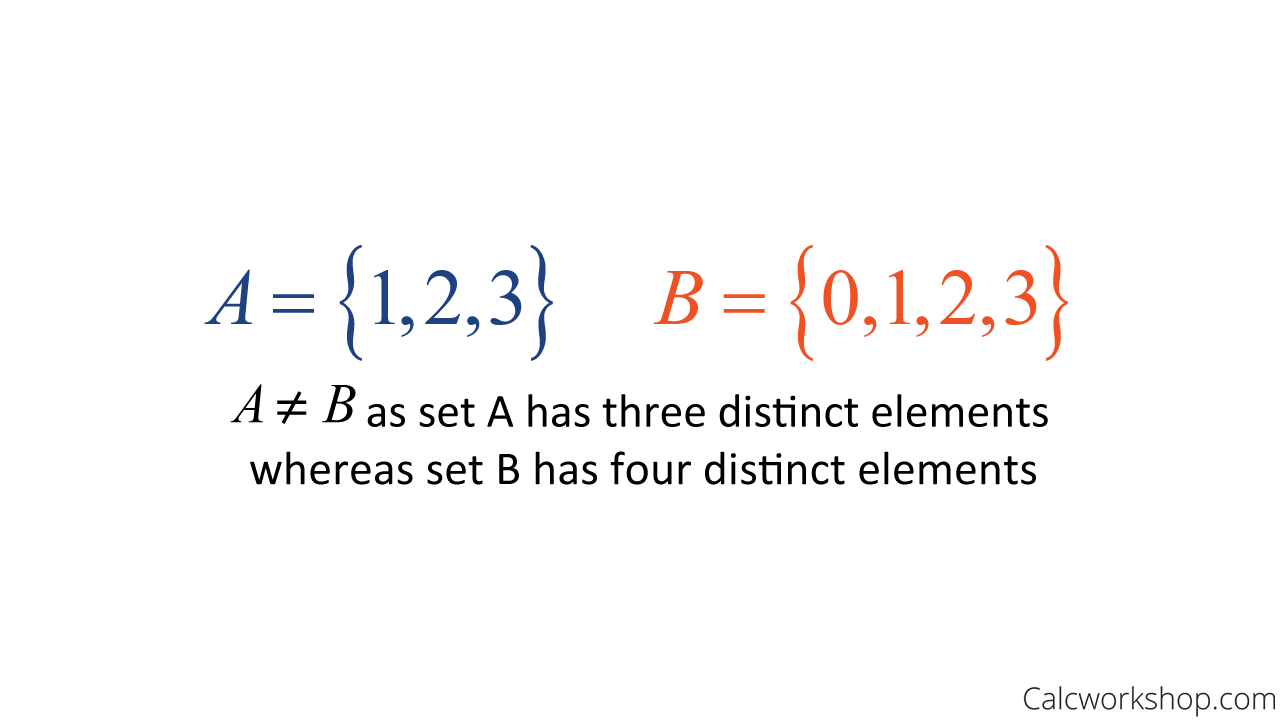
Unequal Sets Example
Equivalent Set
Now, sometimes two sets may not be equal but are equivalent. An equivalent set contains the same number of distinct elements, not necessarily the same elements.
Suppose set A = {1,3,5} and set B = {a, b, c}. While sets A and B are not equal, as they do not contain any of the same elements, they are considered equivalent, as both sets contain three distinct elements.
And now this brings us to some unique sets:
- Universal Set
- Empty Set
- Subsets
- Proper Subsets
To better help us illustrate these ideas, we will use a Venn Diagram.
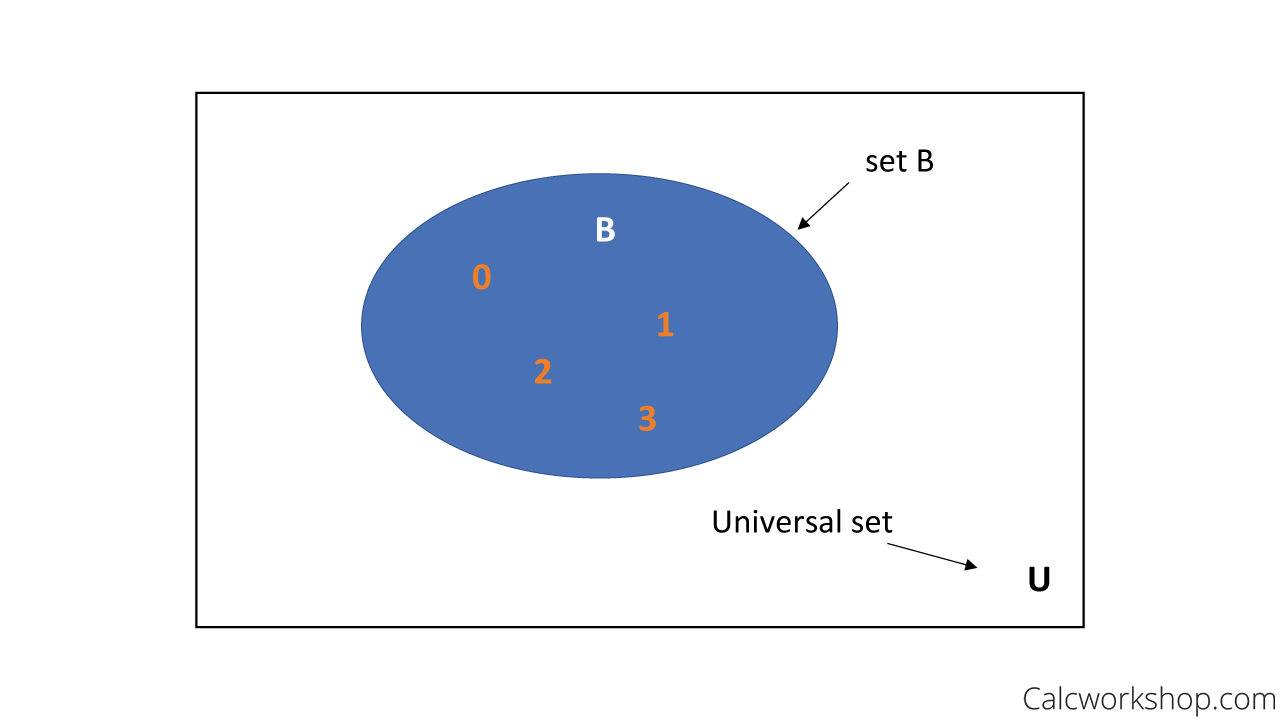
Universal Set Venn Diagram
The universal set contains all the objects or elements under consideration and the empty set, sometimes called the null set, is the set that contains no elements.

Empty Set Symbol
A subset is when the elements of one set are also elements of another collection. For example, set A is a subset of B if and only if every element of A is also an element of B as noted by Lumen Learning.
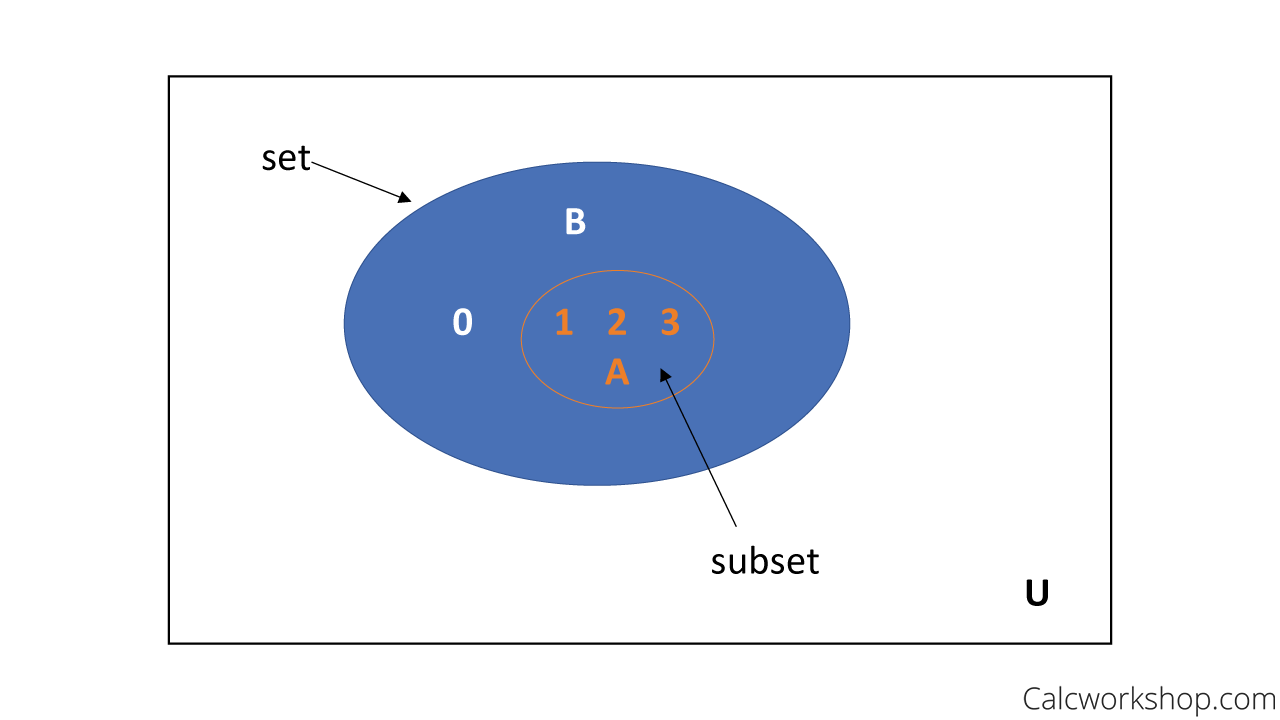
Subset Of Another Set Venn Diagram
Using an example from above, suppose set A = {1, 2, 3} and set B = {0, 1, 2, 3}, then set A is a subset of B because it is a piece of the broader set.

Subset Symbol
And now we’re going to put our thinking caps on as you focus on set A above. Notice that we can say that every element of A is in A. In other words, A is a subset of itself. This means that every set is a subset of itself! Cool, huh?
Now, let’s look at both sets A and B from above. Set A is a subset of A, and B is a subset of B. Furthermore, as we’ve already asserted, set A is a subset of set B.
And this brings us to our next definition… subsets and proper subsets.
A subset is when every element of A is also an element of B. And A is a proper subset of B if and only if every element of A is also in B, as long as A does not equal B. Consequently, using our two sets for A and B above, we can say that A is a proper subset of B because A does not equal B.
Let’s look at another example. Suppose set A = {1, 2, 3} and set B = {0, 1, 2, 3}. Because set A is a subset of B and set A does not equal B, we say that A is a proper subset of B, as there is at least one element in B that is not in A.

Proper Subset Symbol
And did you know that the empty set is a subset of every set? And the empty set is a proper set of every group, except the empty set itself?
Cool!
And now we’re going to focus our attention on the number of subsets. Namely, we are going to discuss cardinality and power sets.
Cardinality
The size of a set is called the cardinality. If there are exactly n distinct elements in A, then the cardinality of A is denoted |A| = n
For example, suppose set V represents the vowels in the English language V = {a, e, I, o, u}. Because there are five distinct letters in the set, we say the cardinality of set V is |V|=5.
So, what is the cardinality of the empty set?
Well, because the empty set represents zero elements, the cardinality of the null set is 0.
Power Set
Now, the formal definition of a power set is to say that the power set considers all combinations of elements of a group. But what does this really mean?
A power set is nothing more than the list of all possible subsets!
In other words, for a given set A, the power set of A is the set of all subsets of A, and is denoted P(A). And we can determine the number of distinct subsets using the formula 2^n, where n represents the number of elements in a set.
For example, let’s find all the subsets of and proper subsets of set S, where S = {winter, spring, summer, fall}. We have to find all the different ways we can create a piece of the broader set.

Power Set Vs Proper Subset
Notice how set S is a subset of itself; hence, the last subset on the left-hand column. In contrast, we do not include set S under the column for proper sets.
Why?
As discussed above, a set is a proper subset as long as it does not equal the collection itself. And that is why there are only 15 possibilities instead of 16.
Additionally, we must note that for set S = {winter, spring, summer, fall}, because there are four distinct elements, the cardinality of S is |S| = 4, and this is what we used to find the number of subsets and proper sets for S.
Cartesian Products
Finally, let’s discuss the concept of Cartesian Products.
Let A and B be two sets. Then the Cartesian Product of A and B, denoted A x B is the set of ordered pairs (a,b) where a is an element of A and b is an element of B.
All this means is that we take each element of the first set and pair it with every element of the second set to form ordered pairs.
For example, suppose for sets A = {apple, banana} and B = {winter, spring, fall}, the A x B and B x A are found as follows.

Cartesian Product Of Sets
Throughout this lesson, we will build upon our knowledge of sets and set the necessary foundation for how we make, define, and distinguish sets and subsets, all while working on numerous examples.
Let’s jump right in!
Video Tutorial w/ Full Lesson & Detailed Examples
1 hr 28 min
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.