In statistical testing, also referred to as hypothesis testing, our goal is to show the credibility of a claim regarding the population.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
What Is Hypothesis Testing
Now it would be unreasonable to assume that we can test the entire population to determine the feasibility of every claim one might have.
Thus, we need a way to conclude an assumption is true or false by taking an appropriate sample and calculating a relevant statistic.
And knowing that we must expect that there will be some variation between the sample statistic that is calculated and the true population parameter, leads us to the understanding of statistical inferences (hypotheses).
Hypothesis Testing Steps
First, we must identify the parameter of interest.
Remember that a parameter always points to the population so that it will be either a population mean, population proportion, population slope, or some other population parameter.
Types of Hypothesis Tests
Then we will write a declaration of our significance test, which will include a null hypothesis statement and an alternative hypothesis.
The null hypothesis is the expected value of the population parameter, similar to the status quo, whereas the alternative hypothesis is a statement of negation of the null hypothesis as discussed by Penn State.
Next, we will calculate the desired test statistic from our random sample. This test statistic is a numerical quantity that measures the difference between the observed value and the expected value, divided by the standard error, which is the sample standard deviation.
Then we will compare this test statistic with a specified level of significance (alpha), just like we did with confidence intervals.
If the probability of yielding the sample statistic is as extreme or more extreme is smaller than our significance level, then we declare the sample statistic to be significant and reject the null hypothesis in favor of the alternative. In other words, if the probability is inside our shaded critical region then it is considered more extreme; thus, rejecting the hypothesis. But if it is outside the critical region, we will fail to reject our claim in favor of the alternative.
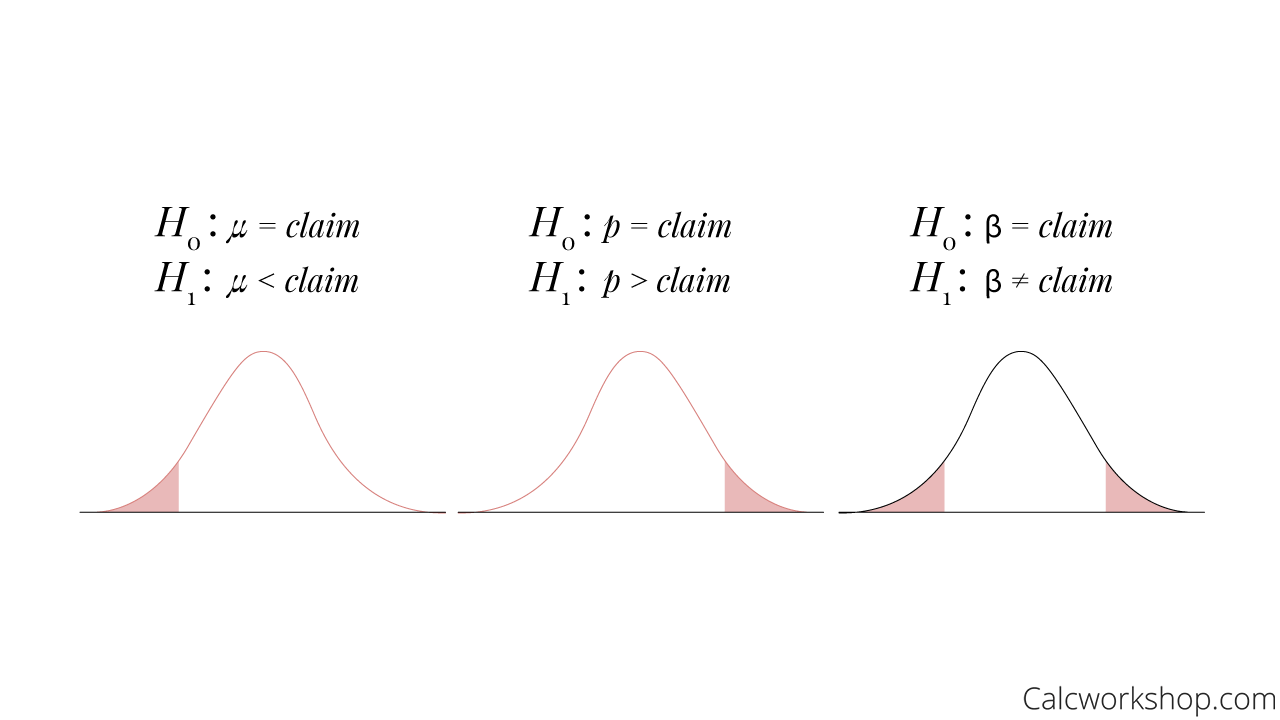
Null and Alternative Hypothesis
Additionally, we will also learn how to determine whether our study calls for a one or two-tailed test.
Type 1 And Type 2 Errors
Now, with all inferences and tests of significance, there is always room for error. A Type I error occurs if we reject the null hypothesis, when in actuality, the null hypothesis is true. Similarly, if we fail to reject the null hypothesis when, in reality, the null hypothesis is false, this is considered a Type II error.

Type 1 Vs. Type 2 Error
Imagine you are in a court of law, where a defendant is presumed innocent until proven guilty. What possible errors could a jury make regarding the outcome of the trial?
First, let’s state the following:
- The Null Hypothesis: The defendant is innocent.
- The Alternative Hypothesis: the defendant is guilty.
Now, a Type I Error would happen if the jury rejects the null hypothesis as false when, in reality, the null hypothesis is true. In other words, the jury finds the defendant guilty of a crime they didn’t commit.
And a Type II Error is when a jury accepts the null hypothesis as true when, in reality, the null hypothesis is false. Meaning, the defendant is found innocent of a crime they did commit.
Let’s look at an example where we put all of these ideas together.
Worked Example
Imagine we have a textile manufacturer investigating a new yarn, which claims it has a thread elongation of 12 kilograms with a standard deviation of 0.5 kilograms.
Using a random sample of 4 specimens, the manufacturer wishes to test the claim that the mean thread elongation is less than 12 kilograms.
Write a hypothesis statement for this scenario and using a normal distribution, find the Type 1 error if the sample mean is less than 11.5 kilograms.
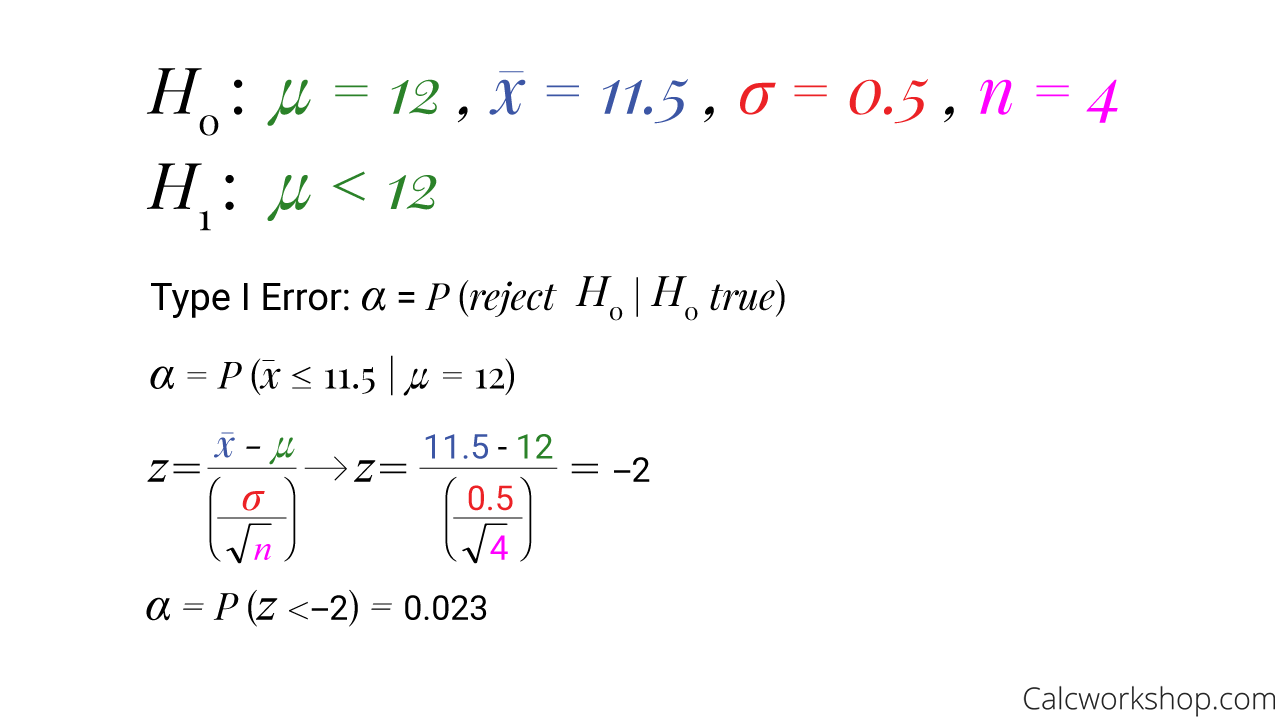
Type 1 Error — Example
As we can see, from the example above, the likelihood of a type I error, where the manufacturer rejects the null hypothesis when the null hypothesis is actually true, is approximately 0.023 or 2.3% likely.
Together, we will look at these two types of error and how they affect decision-making and begin to explore the notion of a probability value and how it helps us determine the validity or falsity of our claim.
Hypothesis Testing – Lesson & Examples (Video)
1 hr 17 min
- Introduction to Video: Statistical Hypotheses
- 00:00:38 – Overview of Hypothesis Testing and determining a correctly stated hypothesis testing problem (Examples #1-7)
- Exclusive Content for Members Only
- 00:14:34 – State the Null Hypothesis and the Alternative Hypothesis for each scenario (Examples #8-12)
- 00:25:46 – Hypothesis Testing Steps and Overview of Type I and Type II errors (Examples #13-14)
- 00:40:32 – Describe a Type 1 and Type 2 error (Examples #15-16)
- 00:46:32 – Overview of p-value and Tails of the Hypothesis Test
- 00:55:55 – Find the probability of a Type I and Type II error (Example #17)
- 01:06:08 – Identify null hypothesis, alternative hypothesis, and state whether the scenario is a one-tail or two-tailed test (Examples #18-21)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.