Did you know that the negative binomial distribution is a sneaky combination of both the binomial and geometric random variables?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Like before, we have this probability of success that will be the same, but there’s a slight twist.
It’s best if we look to an example, here we go!
Suppose Colette is practicing penalty kicks in preparation for an upcoming soccer match. What is the likelihood that she will make her fifth goal on her eighth shot?
This what we are going to be able to find using the Negative Binomial Distribution!
In general, the negative binomial distribution finds the probability of the Kth success occurring on the Xth trial. Alternatively, it finds x number of successes before resulting in k failures as noted by Stat Trek.
What are the conditions of the Negative Binomial Distribution?
Just like we’ve seen for both the binomial and geometric distribution, we will look at the BINS!

Negative Binomial Distribution Mnemonic
Worked Example
So, let’s see how we use these conditions to determine whether a given scenario has a negative binomial distribution.
For example, suppose we shuffle a standard deck of cards, and we turn over the top card. We put the card back in the deck and reshuffle. We repeat this process until we get a 2 Jacks. Is this a negative binomial distribution?
All we have to do is check the BINS!
B – binary – yes, either it’s a Jack or not a Jack
I – independent – yes, because we replace the card each time, the trials are independent.
N – number of trials until you get the kth success – yes, we are told to repeat until we get 2 Jacks.
S – success (probability of success) the same – yes, the likelihood of getting a Jack is 4 out of 52 each time you turn over a card.
Therefore, this is an example of a negative binomial distribution.
Okay, so now that we know the conditions of a Negative Binomial Distribution, sometimes referred to as the Pascal Distribution, let’s look at its properties:
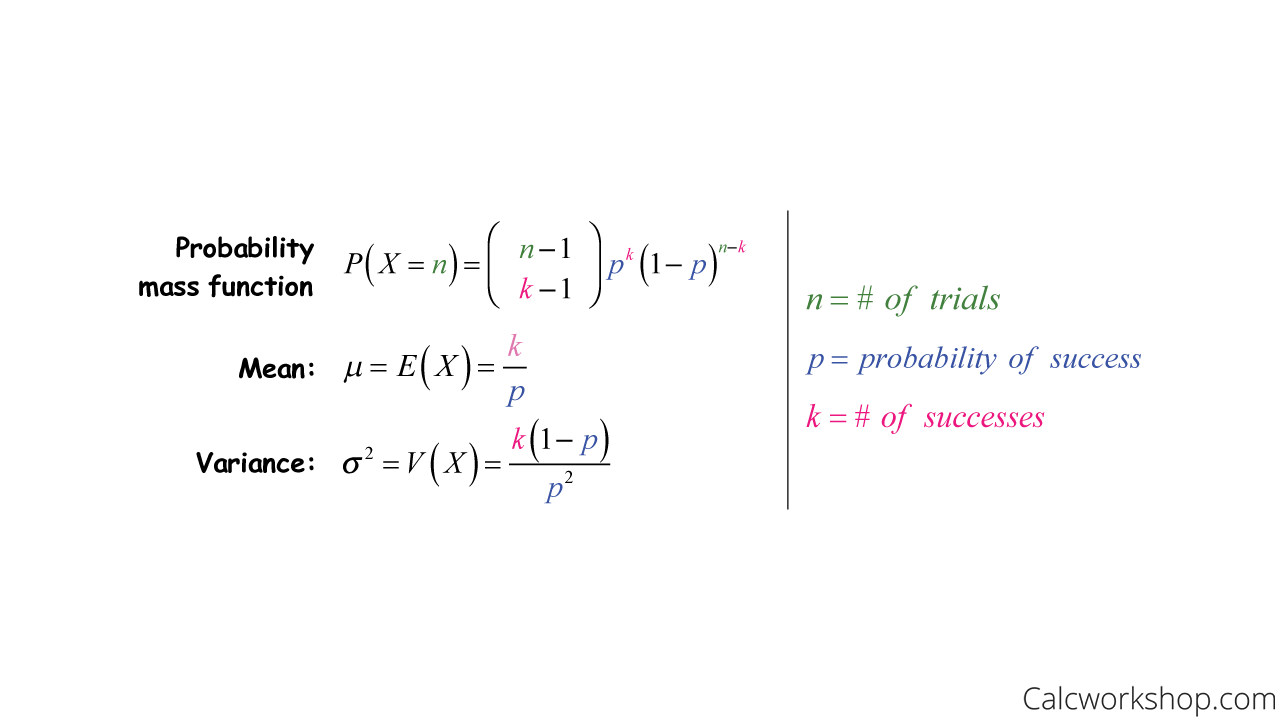
PMF And Mean And Variance Of Negative Binomial Distribution
Notice that the negative binomial distribution, similar to the binomial distribution, does not have a cumulative distribution function. Therefore, if we are asked to find an interval of values, we will have to sum the pmf the desired number of times.
Worked Example
Now, let’s investigate how to use the properties with an example.
Back to Colette and her penalty kicks.
If we are told that the probability Colette scores a goal is 0.78, what is the likelihood that she will make her fifth goal on her eight shot?
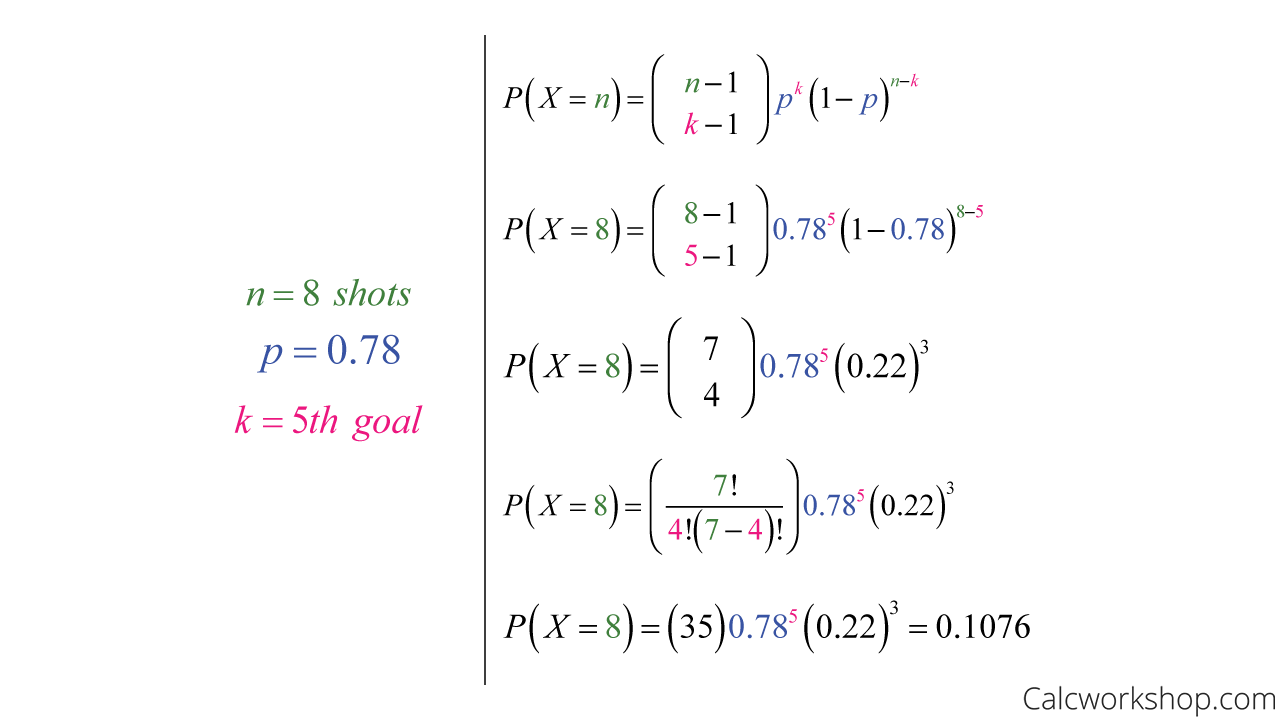
Negative Binomial Probability Example
This means that the likelihood of Colette scoring her 5th penalty kick on her 8th shot is 0.1076.
Now let’s determine the number of shots we would expect Colette to attempt in order to make five goals, as well as the standard deviation.
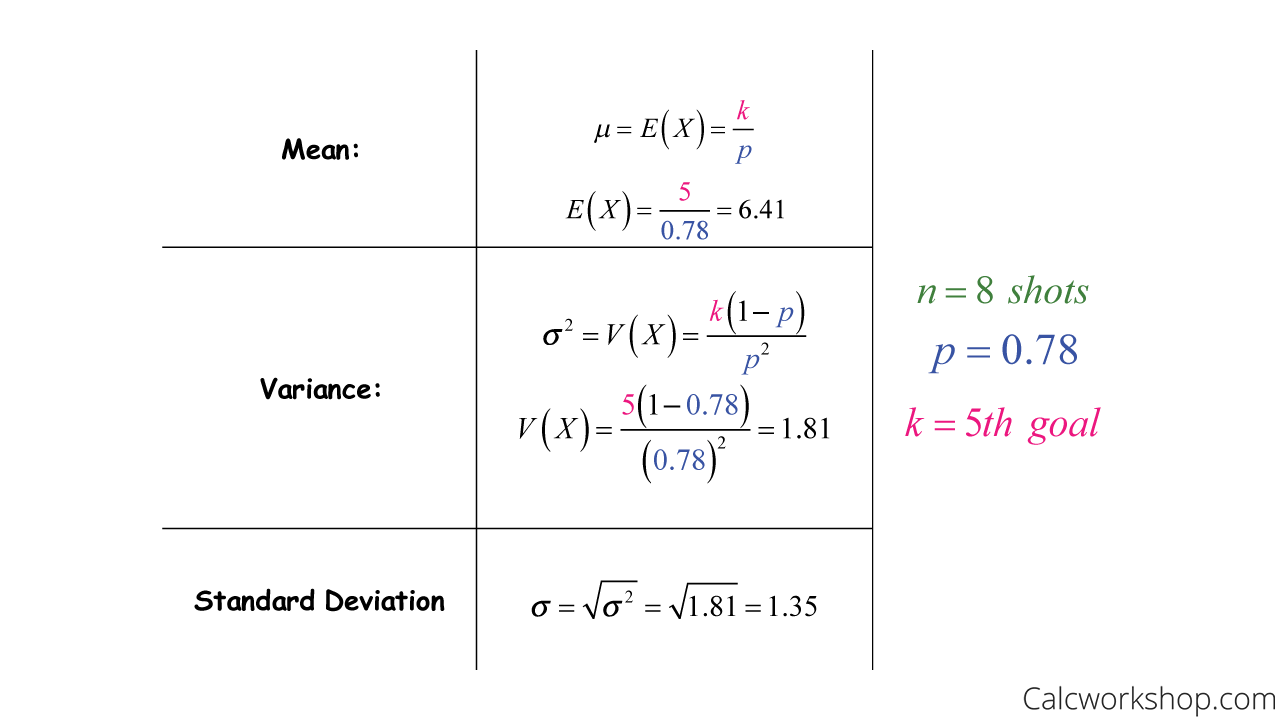
Example Of A Negative Binomial With Mean And Variance And Standard Deviation
What this shows us is that we would expect Colette to take 6.41 shots to make her 5th goal with a standard error or 1.35
And what is interesting to point out is we could have just as easily changed this question from finding Colette’s number of successes to finding the number of failures as well; recognizing that she missed several attempts in her quest to make five penalty kicks.
Throughout this video, we will utilize our conditions for the negative binomial distribution and apply our properties to find expectancy, variance, and probabilities.
Negative Binomial Distribution – Lesson & Examples (Video)
56 min
- Introduction to Video: Negative Binomial Random Variable
- 00:00:32 – What is the Negative Binomial Distribution and its properties?
- Exclusive Content for Members Only
- 00:09:30 – Given a negative binomial distribution find the probability, expectation, and variance (Example #1)
- 00:18:45 – Find the probability of winning 4 times in X number of games (Example #2)
- 00:28:36 – Find the probability for the negative binomial (Examples #3-4)
- 00:36:08 – Find the probability of failure (Example #5)
- 00:39:15 – Find mean, standard deviation and probability for the distribution (Example #6)
- 00:45:42 – Find the probability using the negative binomial and binomial distribution (Example #7)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.