In today’s geometry lesson, we’re going to review Rotation Rules.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
You’re going to learn about rotational symmetry, back-to-back reflections, and common reflections about the origin.
Let’s dive in and see how this works!
A rotation is an isometric transformation that turns every point of a figure through a specified angle and direction about a fixed point.
To describe a rotation, you need three things:
- Direction (clockwise CW or counterclockwise CCW)
- Angle in degrees
- Center point of rotation (turn about what point?)
The most common rotations are 180° or 90° turns, and occasionally, 270° turns, about the origin, and affect each point of a figure as follows:
Rotations About The Origin
90 Degree Rotation
When rotating a point 90 degrees counterclockwise about the origin our point A(x,y) becomes A'(-y,x). In other words, switch x and y and make y negative.
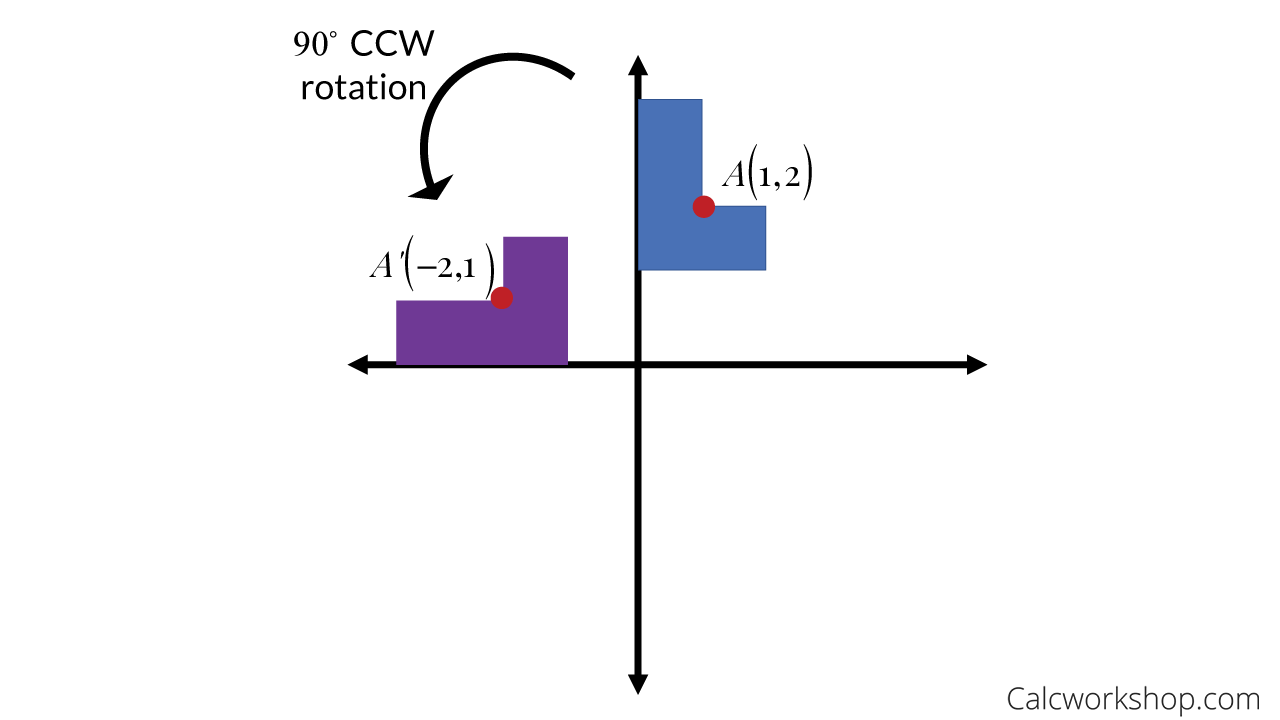
90 Counterclockwise Rotation
180 Degree Rotation
When rotating a point 180 degrees counterclockwise about the origin our point A(x,y) becomes A'(-x,-y). So all we do is make both x and y negative.
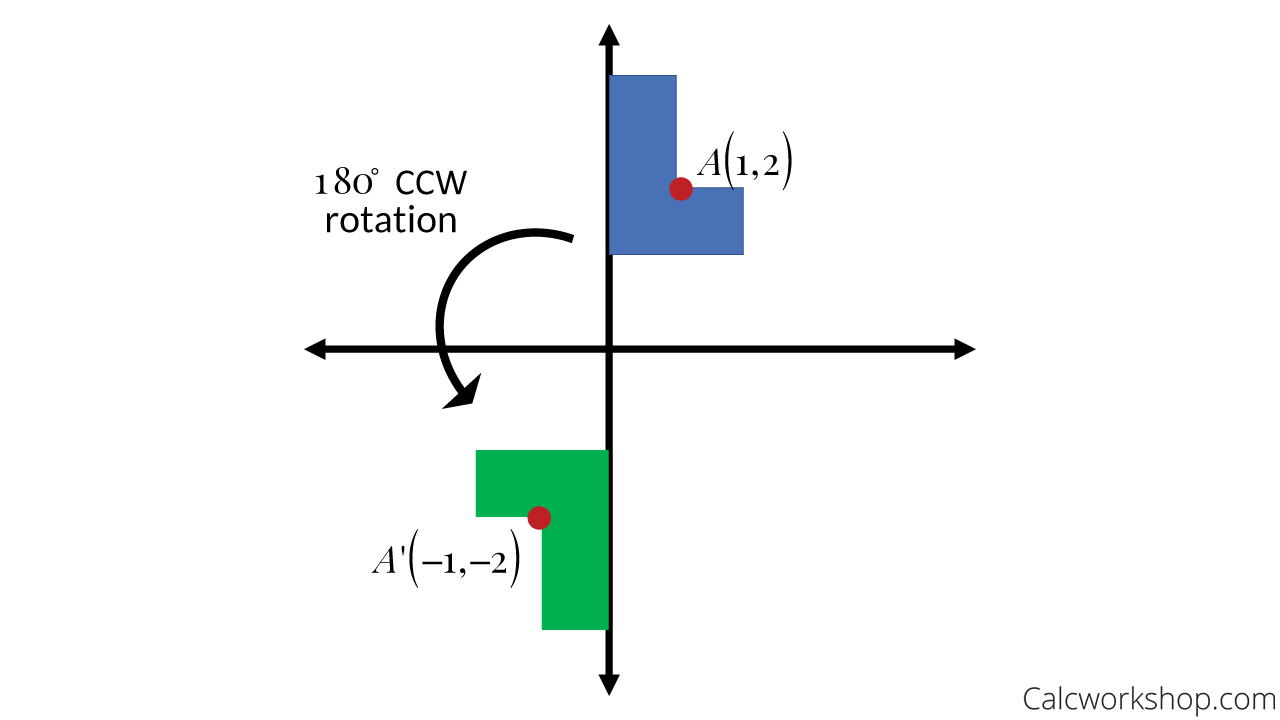
180 Counterclockwise Rotation
270 Degree Rotation
When rotating a point 270 degrees counterclockwise about the origin our point A(x,y) becomes A'(y,-x). This means, we switch x and y and make x negative.
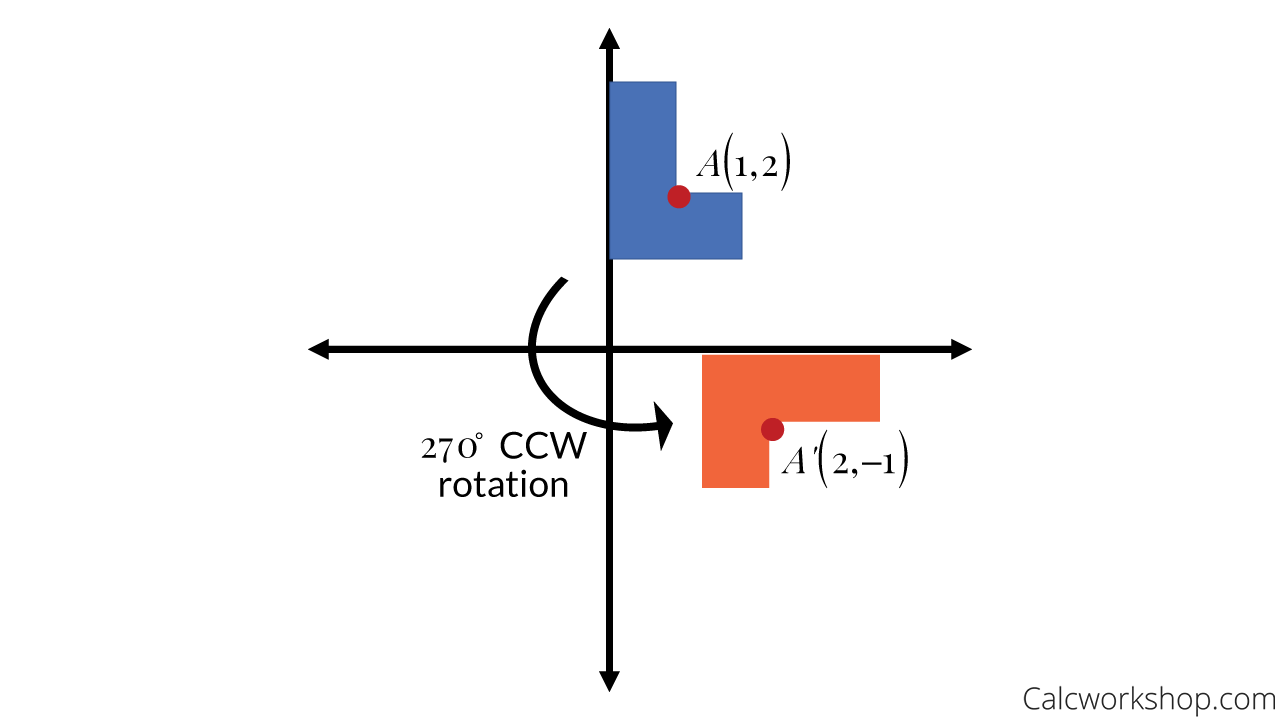
270 Counterclockwise Rotation
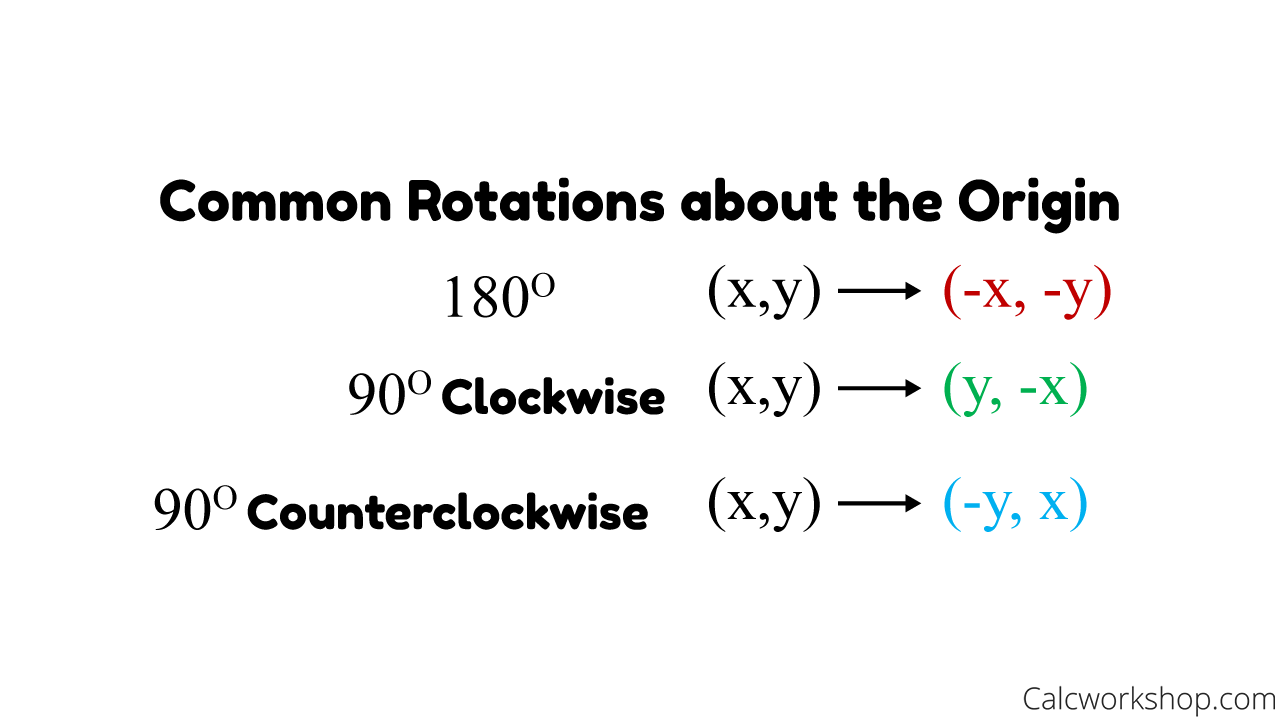
Common Rotations About the Origin
Composition of Transformations
And just as we saw how two reflections back-to-back over parallel lines is equivalent to one translation, if a figure is reflected twice over intersecting lines, this composition of reflections is equal to one rotation.
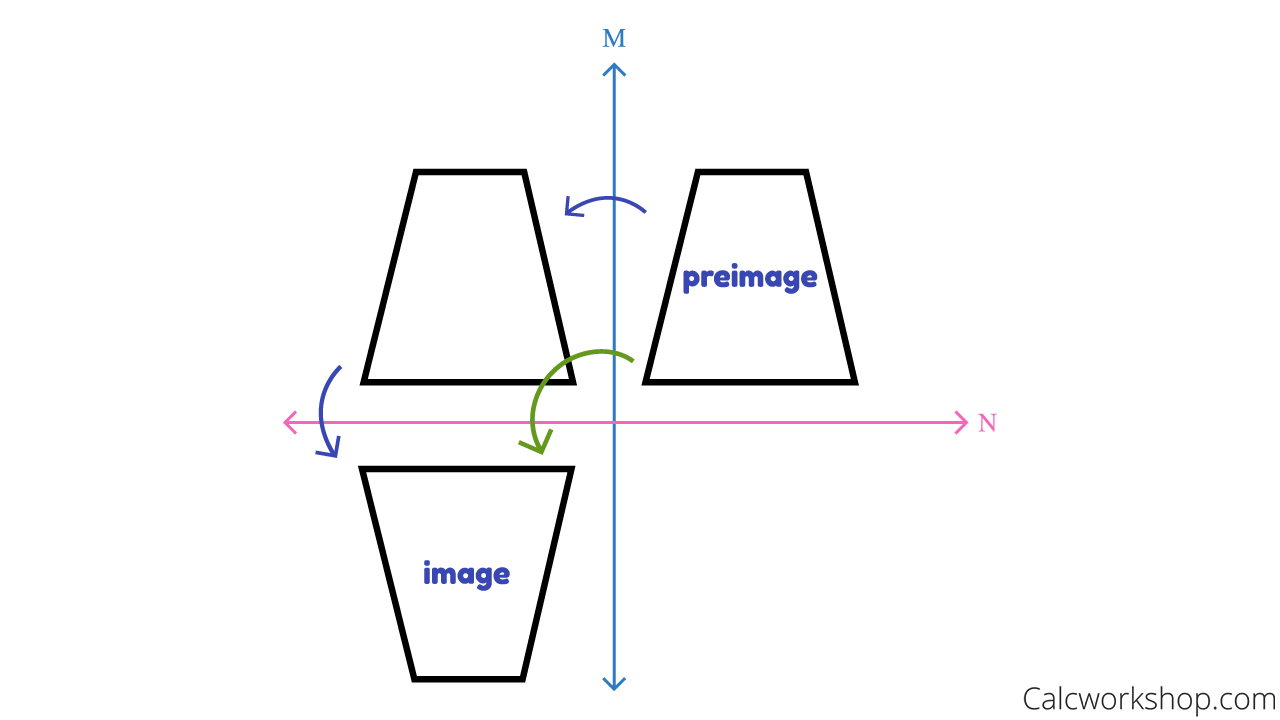
Composition of Transformations
In fact, the angle of rotation is equal to twice that of the acute angle formed between the intersecting lines.
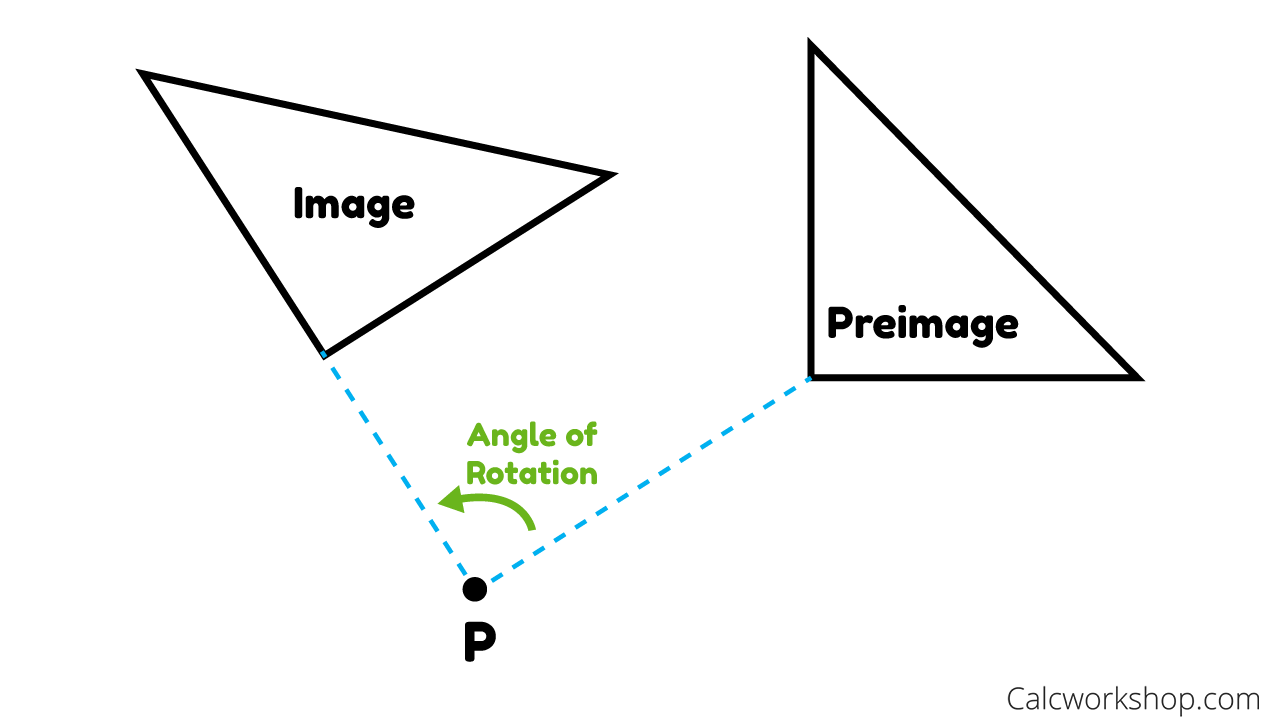
Angle of Rotation
Rotational Symmetry
Lastly, a figure in a plane has rotational symmetry if the figure can be mapped onto itself by a rotation of 180° or less. This means that if we turn an object 180° or less, the new image will look the same as the original preimage. And when describing rotational symmetry, it is always helpful to identify the order of rotations and the magnitude of rotations.
The order of rotations is the number of times we can turn the object to create symmetry, and the magnitude of rotations is the angle in degree for each turn, as nicely stated by Math Bits Notebook.
In the video that follows, you’ll look at how to:
- Describe and graph rotational symmetry.
- Describe the rotational transformation that maps after two successive reflections over intersecting lines.
- Identify whether or not a shape can be mapped onto itself using rotational symmetry.
Video – Lesson & Examples
38 min
- Introduction to Rotations
- 00:00:23 – How to describe a rotational transformation (Examples #1-4)
- Exclusive Content for Member’s Only
- 00:12:12 – Draw the image given the rotation (Examples #5-6)
- 00:16:41 – Find the coordinates of the vertices after the given transformation (Examples #7-8)
- 00:19:03 – How to describe the rotation after two repeated reflections (Examples #9-10)
- 00:26:32 – Identify rotational symmetry, order, and magnitude of the rotation? (Examples #11-16)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.