Did you know that there are 3 types of special parallelograms?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
It’s true!
And in today’s geometry class, we’re going to dive deep into Rectangles, Rhombi, and Squares!
Here we go!
Okay, so have you ever speculated about the difference between a rectangle and a square?
Or wondered about what really is a rhombus?
These words are used by teachers all the time, and we’ve gotten used to hearing them, but what do they really mean and how can we tell the difference between these special quadrilaterals?
Together we are going to put our knowledge to the test, and discover some amazing properties about these three special parallelograms.
Types of Special Parallelograms
First, it is important to note that rectangles, squares, and rhombi (plural for rhombus) are all quadrilaterals that have all the properties of parallelograms.
The biggest distinguishing characteristics deal with their four sides and four angles. A rectangle is a parallelogram with four right angles. A rhombus, which is sometimes called a rhomb or diamond, as Math is Fun nicely states, is a parallelogram with four congruent sides. And a square is a parallelogram with four right angles and four congruent sides.
But there’s more! Let’s take a look at each of their properties closely.
Properties of a square
- All four sides are congruent.
- All four are right angles.
- Diagonals bisect each other.
- Diagonals are perpendicular.
- Diagonals bisect vertices.
- Diagonals are congruent.
- Consecutive angles are supplementary.
Properties of a rhombus
- All four sides are congruent.
- Opposite angles are congruent.
- Diagonals bisect each other.
- Diagonals are perpendicular.
- Diagonals bisect vertices.
- Diagonals are NOT congruent.
- Consecutive angles are supplementary.
Properties of a rectangle
- All four are right angles.
- Opposite sides are congruent.
- Opposite angles are congruent.
- Diagonals bisect each other.
- Diagonals are congruent.
- Consecutive angles are supplementary.
FAQ
Here are some common questions that students have when working on this material.
Q: What is the difference between a rhombus and a parallelogram?
A: For a rhombus we are quaranteed that all the sides have the same length, while a parallelogram only specifies that opposite sides are congruent
Q: What is the difference between a square and a rhombus?
A: A square and a rhombus both have four congruent sides, but a square also has four congruent right angles, whereas a rhombus only specifies that opposite angles are congruent and they do not need to be 90 degrees.
Q: Why is a square a rectangle?
A: A square is a rectangle because it fulfills all the properties of a rectangle. Remember, for a parallelogram to be a rectangle is must have four right angles, opposite sides congruent, opposite sides parallel, opposite angles congruent, diagonals bisect each other, and diagonals are congruent. A square satisfies all of these requirements, therefore a square is always a rectangle.
Q: When is a rhombus a rectangle?
A: A rhombus can be a rectangle only if all four angles of the rhombus are 90 degrees.
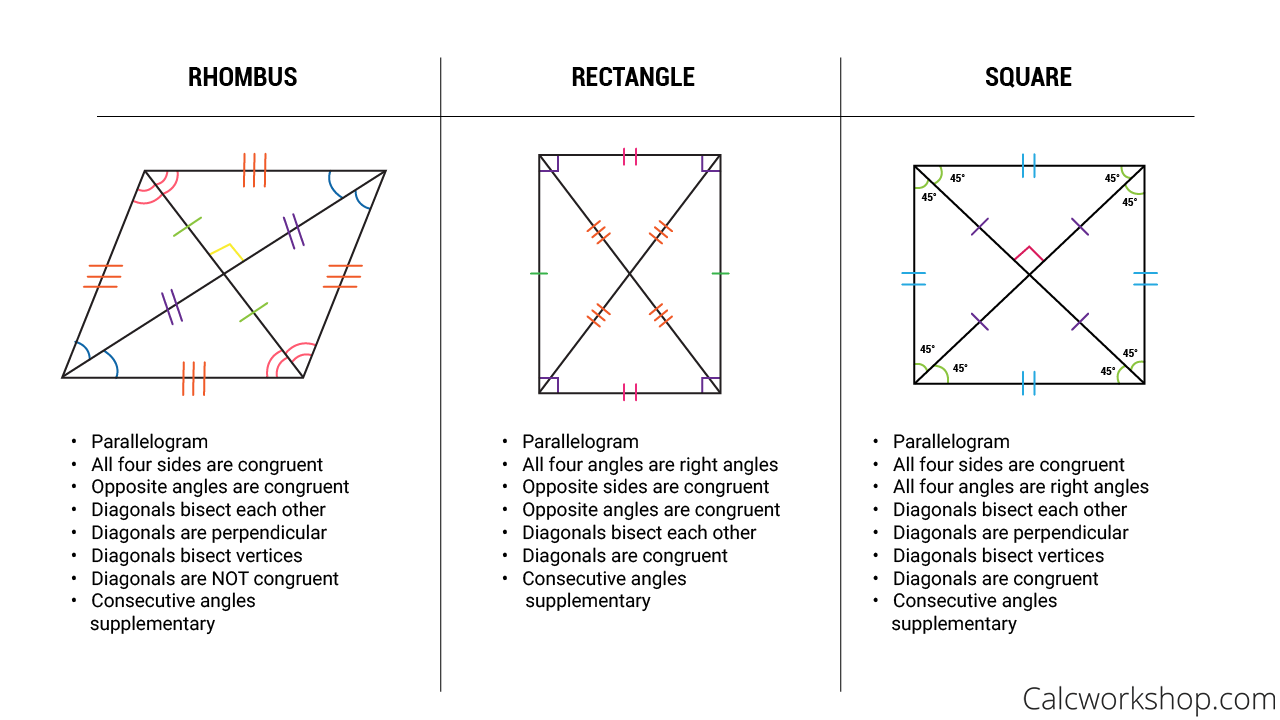
Properties Of Special Parallelograms
Together we will look at various examples where we will use our properties of rectangles, rhombi, and squares, as well as our knowledge of angle pair relationships, to determine missing angles and side lengths.
Additionally, we will draw upon our understanding of Isosceles, Equilateral and Right Triangles to find indicated measures as well as the perimeter of a given polygon.
Special Parallelograms – Lesson & Examples (Video)
43 min
- What are special parallelograms?
- 00:00:21 – How to classify a rhombus, rectangle, and square?
- 00:08:02 – True or False questions: Properties of rectangles, rhombi, and squares (Examples #1-9)
- Exclusive Content for Member’s Only
- 00:15:05 – Given a rhombus, find the missing angles and sides (Example #10)
- 00:23:12 – Given a rectangle, find the indicated angles and sides (Example #11)
- 00:32:38 – Given a square, find the missing sides and angles (Example #12)
- 00:37:48 – Use the properties of a rectangle to find the unknown angles (Example #13)
- 00:41:13 – Use the properties of a rhombus to find the perimeter (Example #14)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.