Inductive Reasoning in Geometry
Easily Explained w/ 11+ Examples!

In today’s geometry lesson, you’re going to learn all about inductive reasoning and its many uses in the mathematical world.

Jenn, Founder Calcworkshop^®, 15+ Years Experience (Licensed & Certified Teacher)

In addition, you’re going to learn how to find patterns, make educated guesses, then prove them true or false.

Let’s go!

Inductive Reasoning

What do the following three characters all have in common?

1. Sherlock Homes
2. Detective William Murdoch
3. Florian Bates

Yes, they are all fictional characters created by the minds of Arthur Conan Doyle, Maureen Jennings, and James Ponti, respectively.

But more importantly, they all use the powers of inductive reasoning to solve mysteries.

As Danielle K. Kincaid, nicely states, inductive reasoning is the ability to extrapolate observed information in order to arrive at conclusions about events that have not been observed.

All three of the above mentioned characters use their powers of observation to gather information about a crime scene to arrive at a conclusion – that may or may not be correct.

But, the more information they gather, combined with their extensive knowledge of facts, help them make the necessary connections that almost always arrive at the correct solution.

And this power of observation, and information gathering, is what inductive reasoning is all about!

So what do Sherlock Holmes, William Murdoch, or Florian Bates have to do with Geometry?

Well, just like these great detectives, we too are going to put our thinking caps and use the power of inductive reasoning to draw conclusions

Much of geometry consists of three stages:

1. Recognizing patterns
2. Making a conjecture
3. Verifying the conjecture

And inductive reasoning is the process of generalizing, looking for patterns, and forming ideas to help us explain things around us.

Inductive vs Deductive Reasoning

Before we move on, we first need to clarify the differences between inductive and deductive.

Inductive reasoning uses patterns and observations to draw conclusions, and it’s much like making an educated guess. Whereas, deductive reasoning uses facts, definitions and accepted properties and postulates in a logical order to draw appropriate conclusions.

Conjecture

A mathematical conjecture is a statement made without conclusive proof but is a type of hypothesis or educated guess. As SparkNotes accurately states, inductive reasoning helps us organize what we observe into succinct hypotheses that we can prove using other, more reliable methods.

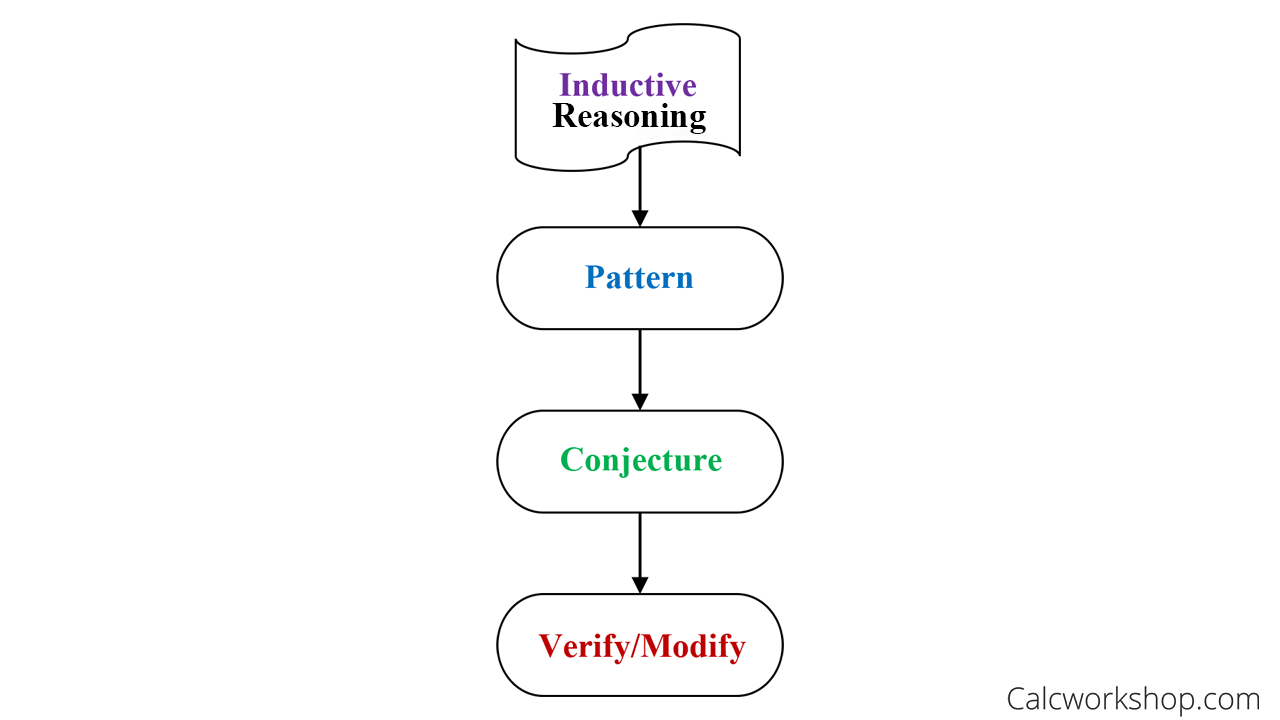
Inductive Reasoning Process

But, with inductive reasoning, we become math detectives and look for patterns, notice similarities, and draw conclusions that can be proved later. The most important part is that we’re “thinking” and trying to find a logical conclusion for what we observe.

Counterexample

Now not all statements or conjectures are true. The easiest way to disprove a statement or proposition is to provide a counterexample.

A counterexample is an one example that disproves a statement. And the cool thing about counterexamples is that you only need to provide one example, even if there are many.

For example, if someone said, “all books have pictures in them.”

You can then provide a counterexample of a novel (you only need one) that does not have pictures; thus, proving that this statement is false.

Or let’s say someone claims “all cats have fur.” You can then say that the Sphynx cat does not have fur; hence, providing a counterexample to the aforementioned proposition.

So together we are going to look at patterns to predict future numbers, make conjectures, or find counterexamples that prove a conjecture is false.

Get ready, because the game is afoot!

What is Inductive Reasoning? – Lesson & Examples (Video)

22 min

• Introduction to inductive reasoning
• 00:00:21 – What are conjectures & counterexamples? (Examples #1-3)
• Exclusive Content for Member’s Only

• 00:05:34 – Using inductive reasoning to make conjectures (Examples #4-7)
• 00:15:37 – Show that each conjecture is false by finding a counterexample (Examples #8-12)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions