As we already know, when simplifying a radical expression, there can not be any radicals left in the denominator.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Rationalizing is the process of removing a radical from the denominator, but this only works for when we are dealing with monomial (one term) denominators.
How do we rationalize a binomial denominator?
We use conjugates!
The conjugate, or conjugate pair, is when we change the sign in the middle of two terms.
Why do we do this?
Just like how we saw with the difference of two squares, when we multiply two radical binomials together that are conjugates we will get a result that no longer contains any radicals, as Purple Math nicely states.
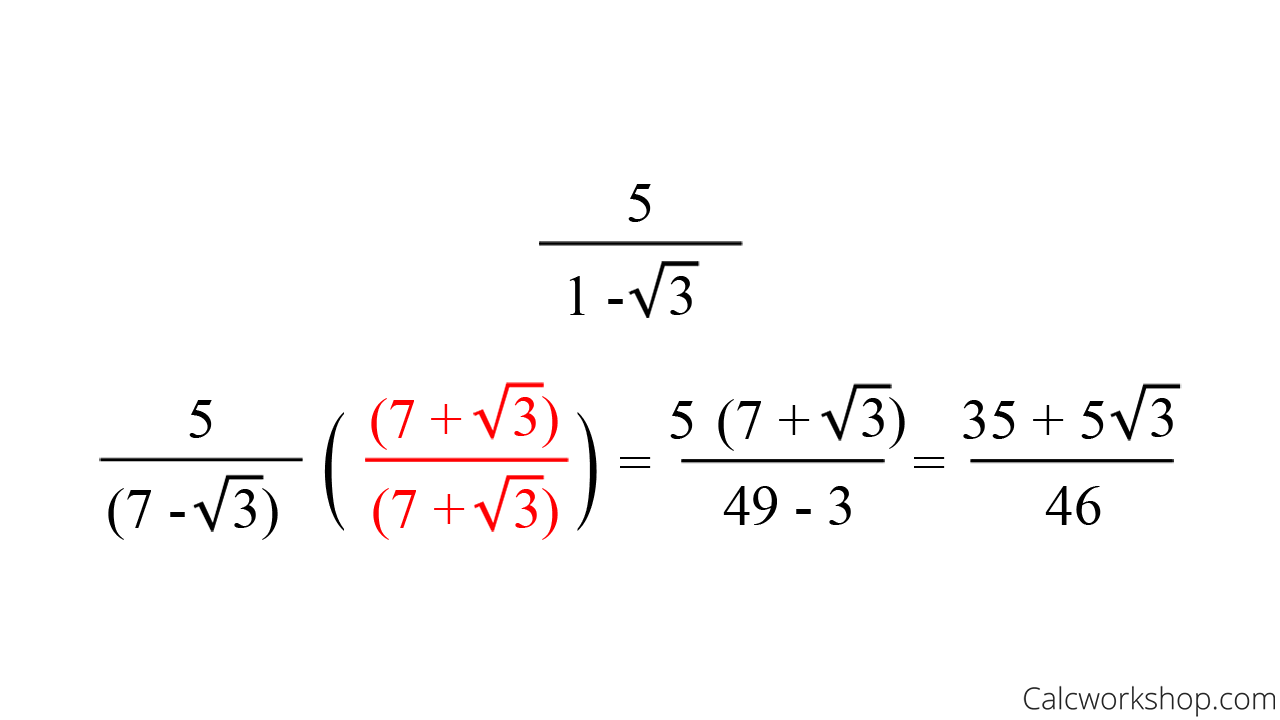
Example of How to Apply the Conjugate
Together we will learn how to accurately apply the conjugate to radical binomials and successfully rationalize both numerators and denominators with this incredibly powerful technique.
Why is understanding conjugates so important?
Because you will use this process in solving trig identities, evaluating limits, and complex solutions. In fact, the way we find the purely real number from a complex value is to use a complex conjugate.
The process of conjugates is universal to so many branches of mathematics and is a technique that is straightforward to use and simple to apply.
Conjugate Math (Explained) – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.