When simplifying radicals there are certain rules that we must follow.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
We must ensure that the radicand has no factor raised to a power greater than or equal to the index, and that the exponent in the radicand and the index have no common factors.
Likewise the radicand must not contain fractions and no denominator should contain a radical.
So how do we get rid of any radical in the denominator?
We rationalize!
Rationalizing the denominator is accomplished by multiplying top and bottom by the square root found in the bottom. In essence, we are merely multiplying by a form of 1.
The process is super easy to follow, and we can use the process of rationalizing for numerical and variable radicands.
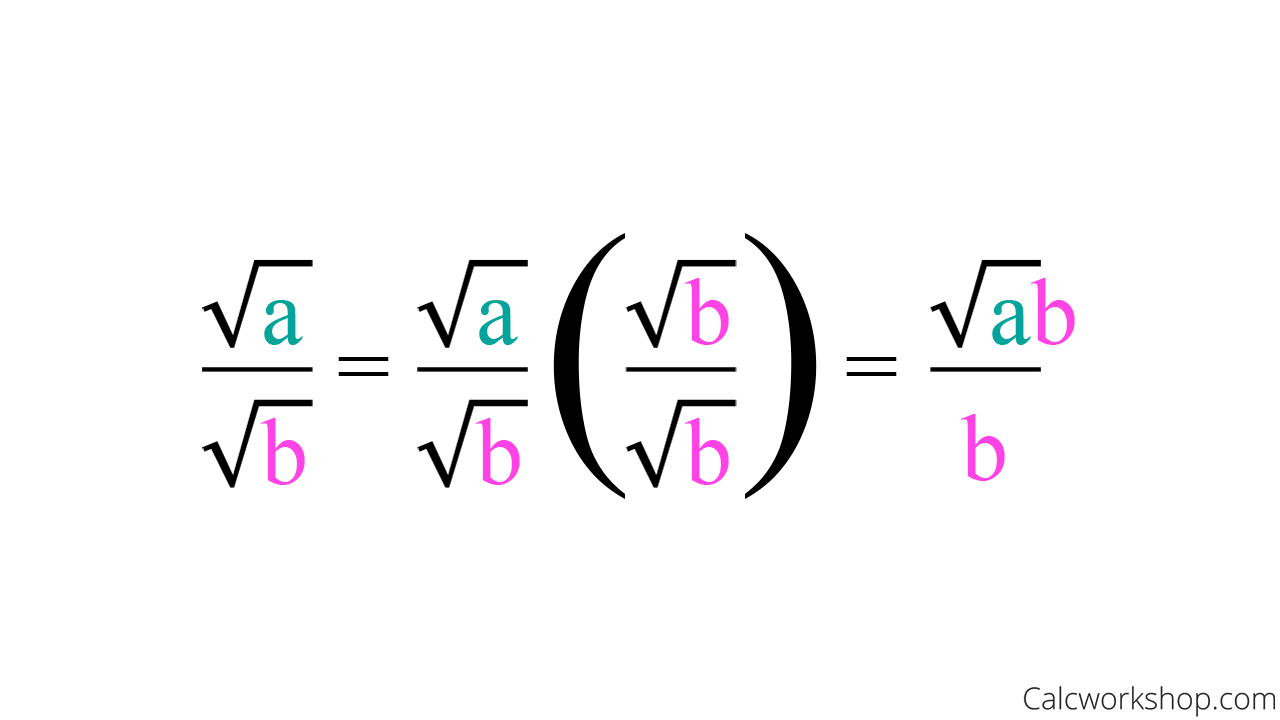
Rationalizing Square Root Denominators
Remember, our overall goal is to get rid of the radical in the denominator in order to change the denominator into a rational (i.e., whole number or fractional) value, as Purple Math nicely states.
But, please keep in mind that this process of multiplying top and bottom by the same radical found in the denominator only applies to square roots.
So what do we do when we have a cube root, fourth root, etc., in the denominator?
We convert from a radical to a rational exponent and multiply by a factor that will ensure that the addition of exponents equals one.
Now some of you may be thinking… why do we even have these rules about radicals?
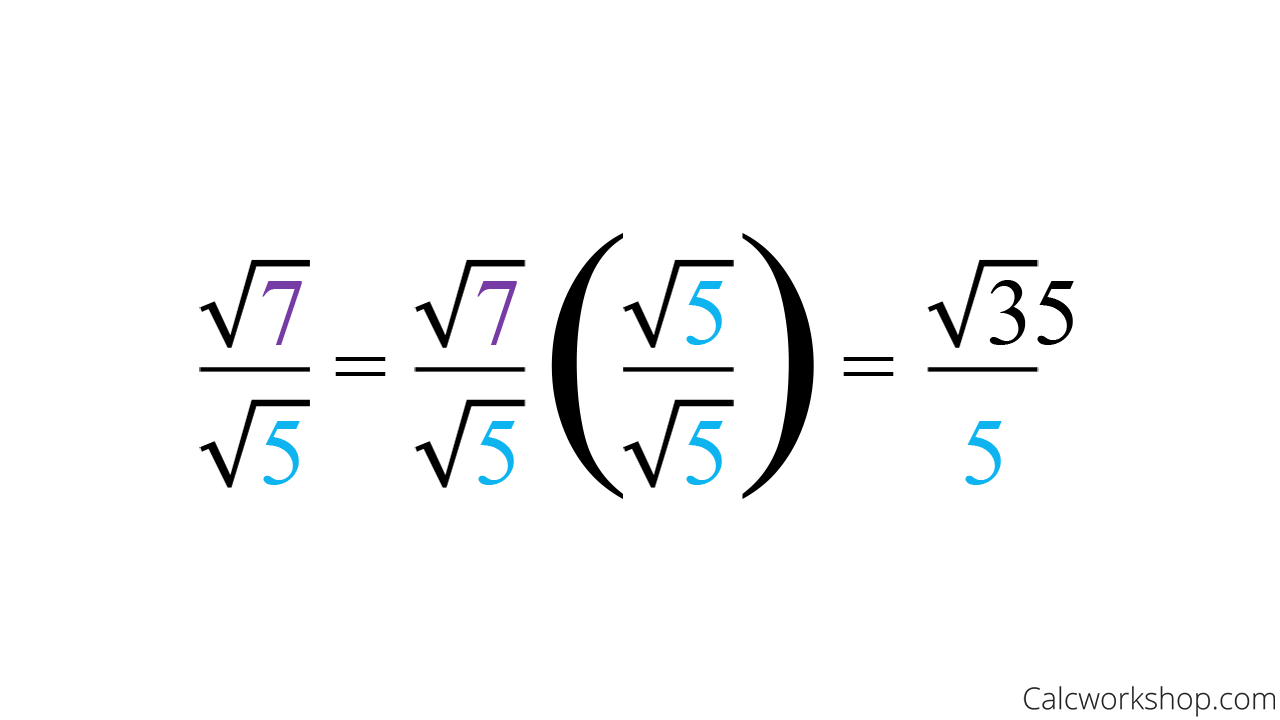
Example of How to Rationalize a Denominator
What’s wrong with having a radical in the denominator?
Nothing!
Truly, there really isn’t anything wrong with having a radical in the denominator, and there will come a time when rationalizing isn’t necessary. But, understanding the process of rationalization is a very useful skill and will come in handy in future math classes.
Moreover, it is easier to estimate values of radical expressions when the radicals are only in the numerator.
Besides, it looks nicer!
So, together we will look at 19 examples of how to rationalize the denominator and simplifying all different types of radicals.
Rationalizing (How-To) – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.