Will we ever be given a differential equation where we can not use separation of variables?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Yes. In fact, there are several ways of solving differential equations, but sometimes even these methods which you will learn in future lessons will sometimes fail or be too difficult to solve by hand.
Is there a method for solving ordinary differential equations when you are given an initial condition, that will work when other methods fail?
Yes! Euler’s Method!
From our previous study, we know that the basic idea behind Slope Fields, or Directional Fields, is to find a numerical approximation to a solution of a Differential Equation.
Euler’s Method, is just another technique used to analyze a Differential Equation, which uses the idea of local linearity or linear approximation, where we use small tangent lines over a short distance to approximate the solution to an initial-value problem.
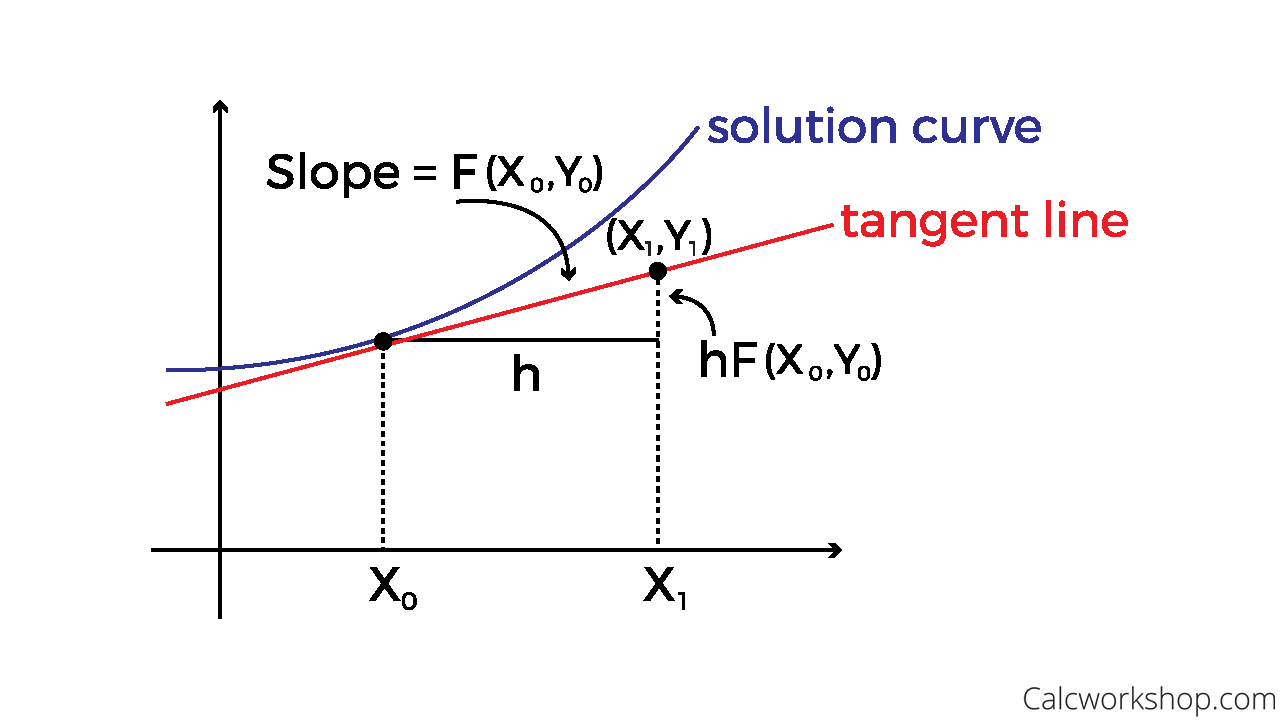
Euler’s Approximation
Remember.
That if we zoom in small enough, every curve looks like a straight line, and therefore, the Tangent Line is a great way for us to calculate what is happening over a period of time.
With this idea, we embark on our study of Euler’s Method.
As SOS Math nicely states, with this idea that, close to a point, a function and its tangent line do not differ very much, we will obtain numerical approximations to a solution.
We will begin by learning Euler’s Method Formula.
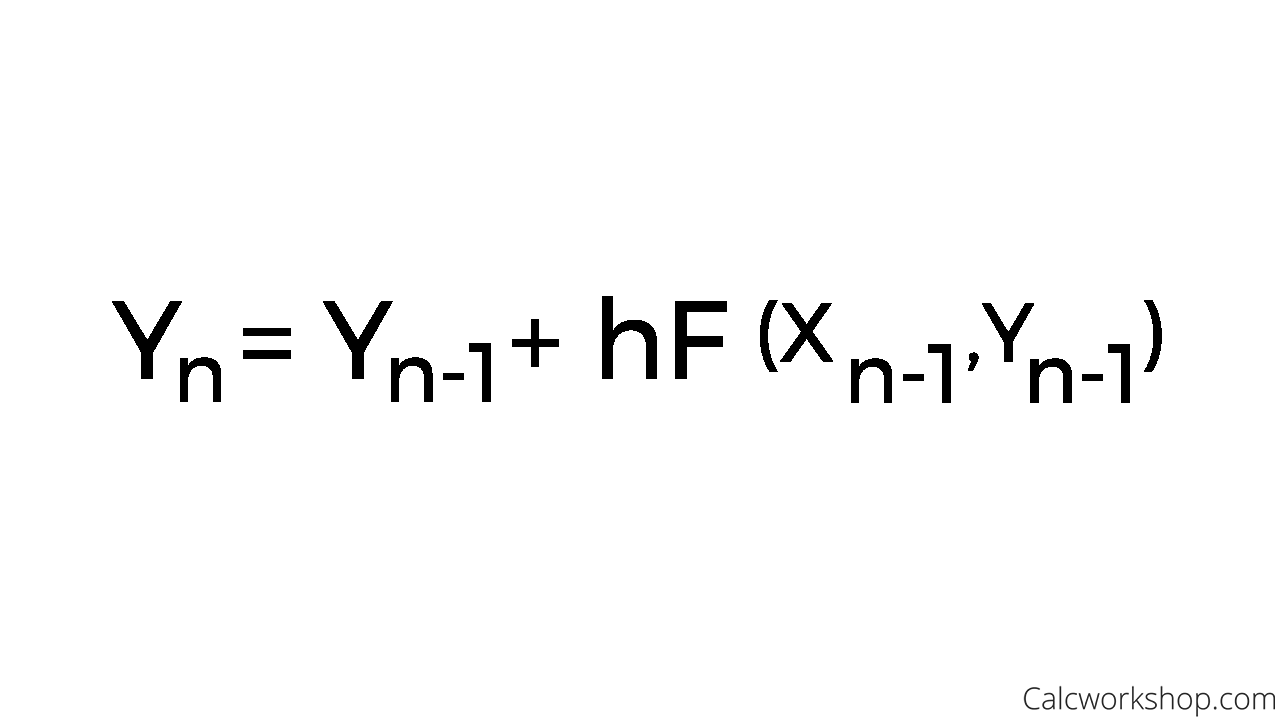
The Formula for Euler’s Method
Then we’ll improve upon this method by using a tabular approach, thus making calculating numerically easy and organized.

Euler’s Method via Table
But there comes a warning…
…Euler’s Method will only be accurate over small increments and as long as our function does not change too rapidly.
Consequently, we need to ensure that our step-size isn’t too large or our numerical solution will be inaccurate.
Together we will solve several initial value problems using Euler’s Method and our table by starting at the initial value and proceeding in the direction indicated by the direction field.
Lastly, we will then look a question where we compare our three techniques for Differential Equations:
- Slope Fields.
- Euler’s Method.
- Finding particular solutions via Separable Differential Equations.
Euler’s Table Method – Video
