Wouldn’t it be nice if when we’re given a nasty, complicated fraction and we could just break it up into two or more smaller, friendly fractions.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Well, the process of Partial Fraction Decomposition, or Partial Fractions, is how we go about taking a rational function and breaking it up into a sum of two or more rational expressions.
In other words, we’re going to “decompose” the big fraction to get the sum of two or more smaller fractions!
But why would we want to?
Well, in Calculus and Differential Equations, this technique is going to be one of the most useful and efficient ways of integrating, so we definitely want to learn the basics now!
Okay, so how do we go about taking a rational expression (i.e., a fraction) and breaking it up into a sum of two or more smaller fractions?
There are three steps!
Step #1: First, we have to check our degrees.
What’s a degree again? It’s the largest exponent on a variable.
And, remember when we learned how to find the horizontal or oblique asymptotes for Rational Functions? Well, we will be using this same knowledge to determine whether we have a fraction in simplified form (i.e., the degree of the bottom is bigger than the degree of the top).
If the degree of the top is equal to or greater than the degree of the bottom, that means our fraction is not proper, as Math is Fun accurately states; therefore, we must simplify by using Long Division… don’t worry, I’ll walk you through it!
Step #2: Then we will factor our denominator and look at our factors.
There are four different types of factors we will be investigating:
- Distinct, Linear Factors
- Repeated, Linear Factors
- Distinct, Non-Linear (quadratic) Factors, and
- Repeated, Non-Linear Factors
Once we’ve determined which category our denominator falls under, we will learn exactly how to write our smaller fractions, and identify how many constants we will need to find.
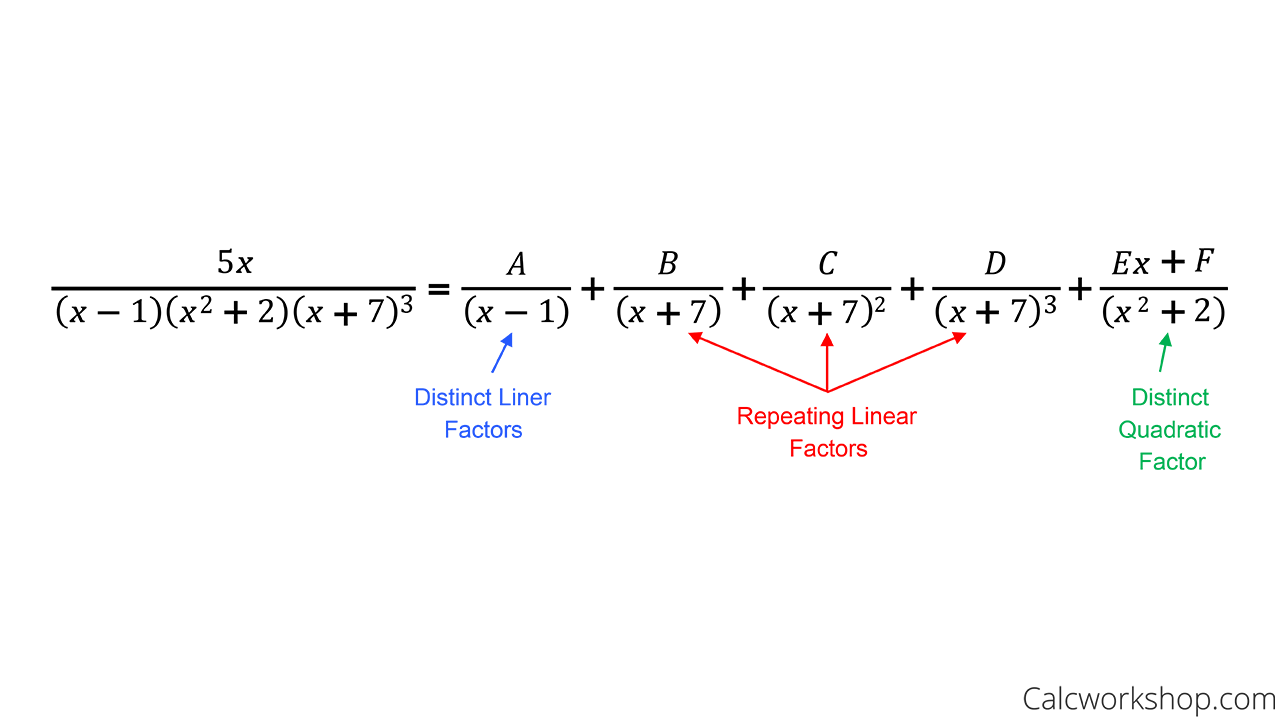
Example of How to Create Partial Fractions
And, we are going to make a HUGE connection between precalculus and calculus in terms of how we come up with each constant … they have everything to do with Derivatives!
It’s super exciting!
Step #3: Use your Algebra techniques to solve for the constants.
What do we mean by “algebra techniques”? It’s a fancy way of saying, solve the equation!
Now, there are two ways of doing this:
- Plugging in the zeros from your factors
- Comparison (equating) method
Don’t worry, I’ll show you how to do both!
And that’s it!
Together we will look at each step in detail and then apply them to six examples!
Partial Fractions (How-To) – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.