Have you ever run across a derivative that you couldn’t take directly, and you felt like throwing up your hands in frustration?

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
Don’t worry — we’ve all been there.
In fact, there are countless instances when direct differentiation (i.e., power rule, chain rule, quotient rule, etc.) is such a beast that we should look for a different method.
That’s when the logarithmic differentiation comes into play!
We use this method when the ordinary rules of differentiation seem algebraically complicated.
For instance, which do you think would be easier to differentiate?

Log – Condensed Vs Expanded Form
Now, at first glance, you may be tempted to say the left side because it’s all one term.
But after further inspection, I hope you will recognize that it’s the function on the right since it’s only a simplified version of the left. That also makes it much easier to calculate!
Here’s why.

Derivative – Log Condensed Vs Expanded Form
By using the properties of logarithms, the right side ended up being much more manageable.
So, when it’s about to get complicated, pull out those log properties.
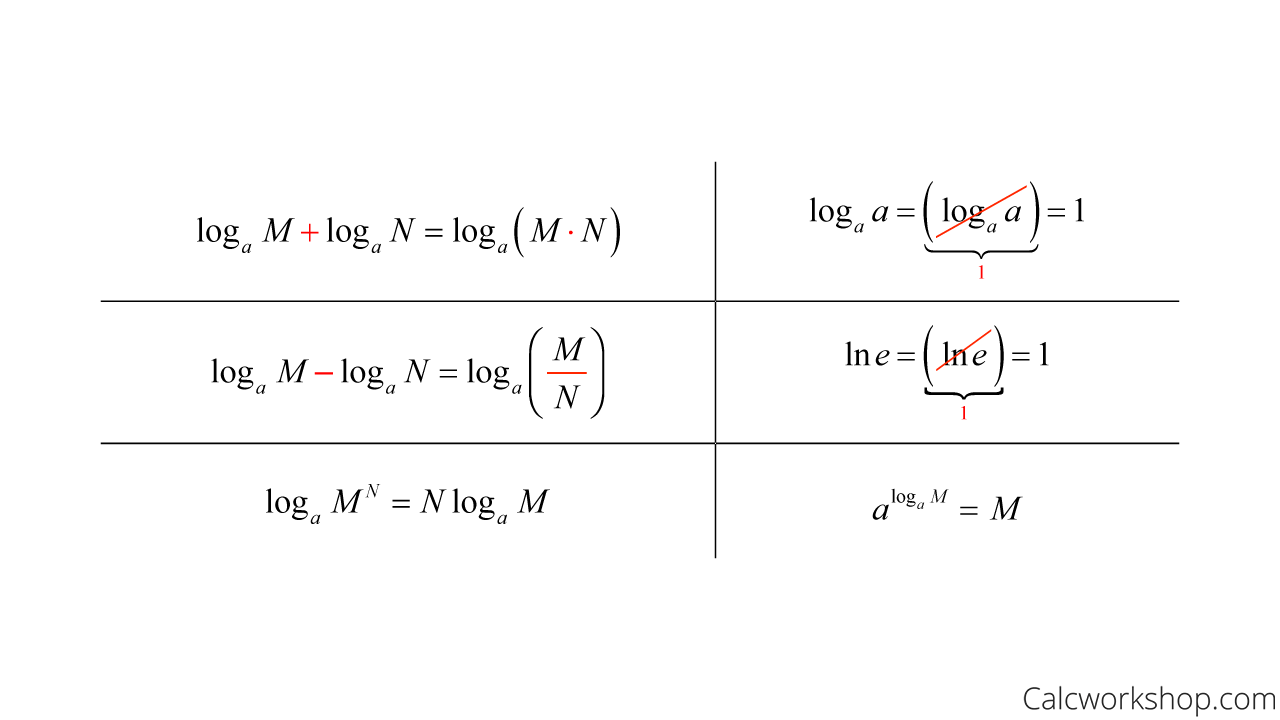
Properties Of Log Functions
Logarithmic Differentiation Steps
But what happens if we are given a function that isn’t logarithmic — can we still use this method to make taking derivatives easier?
You bet.
Just follow the five steps below:
- Take the natural log of both sides.
- Use log properties to simplify the equations.
- Differentiate both sides using implicit differentiation and other derivative rules.
- Solve for dy/dx.
- Replace y with f(x).
Example
For instance, finding the derivative of the function below would be incredibly difficult if we were differentiating directly, but if we apply our steps for logarithmic differentiation, then the process becomes much easier.
Take a look!
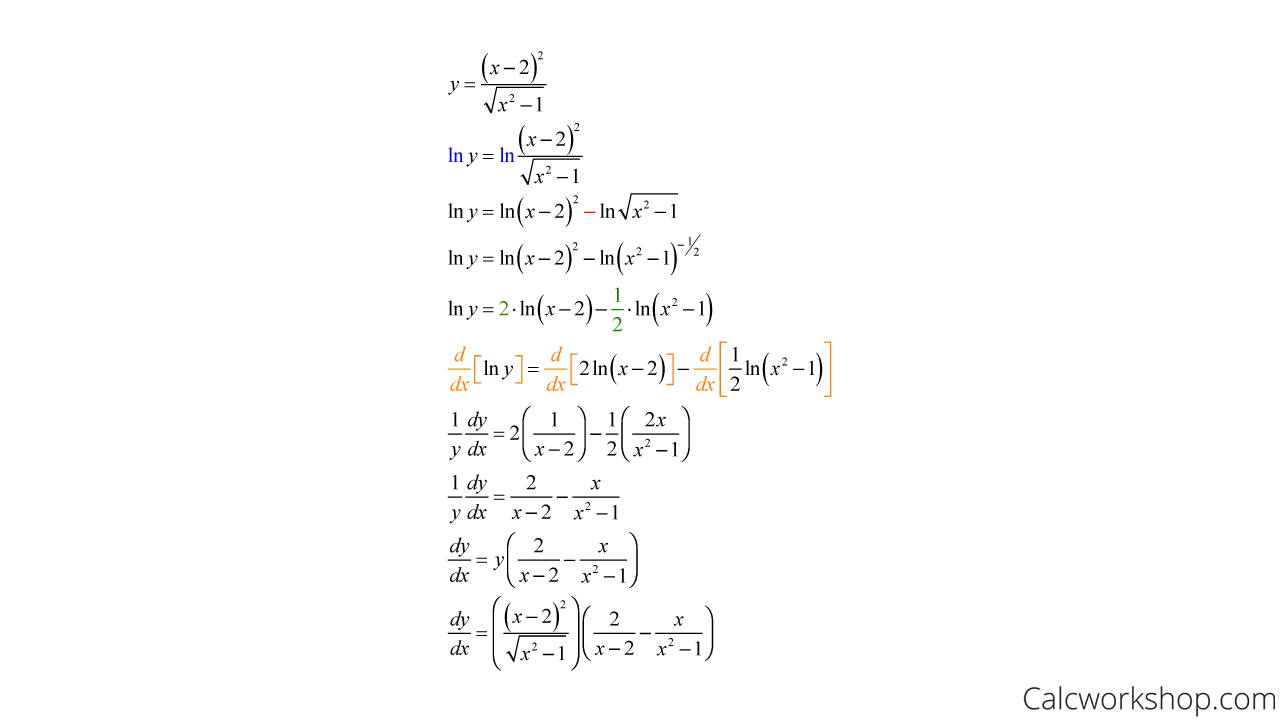
Logarithmic Differentiation – Example
So, all we did was take the natural logarithm of both sides of the equation, apply the logarithm properties to separate terms, differentiate implicitly, and simplify.
Example
While logarithmic differentiation can help us with algebraically tricky questions, this technique’s real power is when we are given an expression where one variable is raised to another variable — and the normal rules for derivatives don’t apply.

Function Raised To A Function
Rewrite the equation so that the variables are no longer exponents with the help of logarithmic differentiation.

Function Sin X Raised To 2x Power
Notice that the variable, x, appears as the base and the exponent. Therefore, the usual rules of direct differentiation don’t apply.
Consequently, we need to follow the steps for logarithmic differentiation.
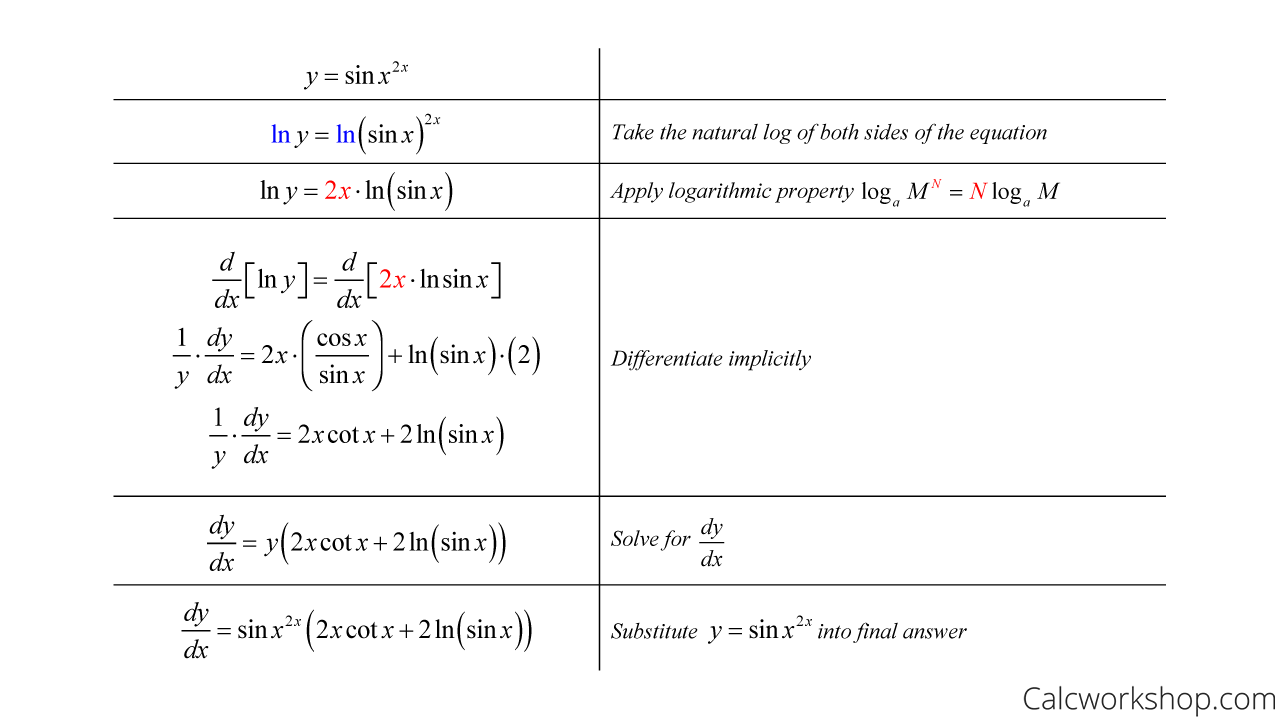
Logarithmic Differentiation Of Trig Functions
It’s that simple!
Together we will look at five questions involving polynomials, trig, exponentials, and of course, log functions, as we learn how to apply logarithmic differentiation with ease.
Let’s jump to it!
Video Tutorial w/ Full Lesson & Detailed Examples (Video)

Boost Your Calculus Scores with Step-by-Step Instruction
Jenn’s Calculus Program is your pathway to confidence. Each lesson tackles problems step-by-step, ensuring you understand every concept.
No more knowledge gaps – Jenn’s instruction bridges the missing pieces, so you’re always in stride with your class.
Calculus won’t block your academic or professional goals. Lay a solid foundation, one lesson at a time.
Your path to calculus success is just one click away.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.