A Parabola is nothing new to us. We’ve been graphing Quadratic Functions for a long time.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
So what else is there to know?
Well, if we slice a right circular cone with a plane we form the Parabolic Conic Section.
So?
All right, well a Parabola, as you already know is pretty easy to graph and we can find our vertex and zeros (x-intercepts) quite easily, and we also know how it will open (up, down, left or right).
But what is so super-duper cool about a Parabola is that every point on the curve is equidistant from a fixed point, called the Focus, and a fixed line, called the Directrix.
Huh?
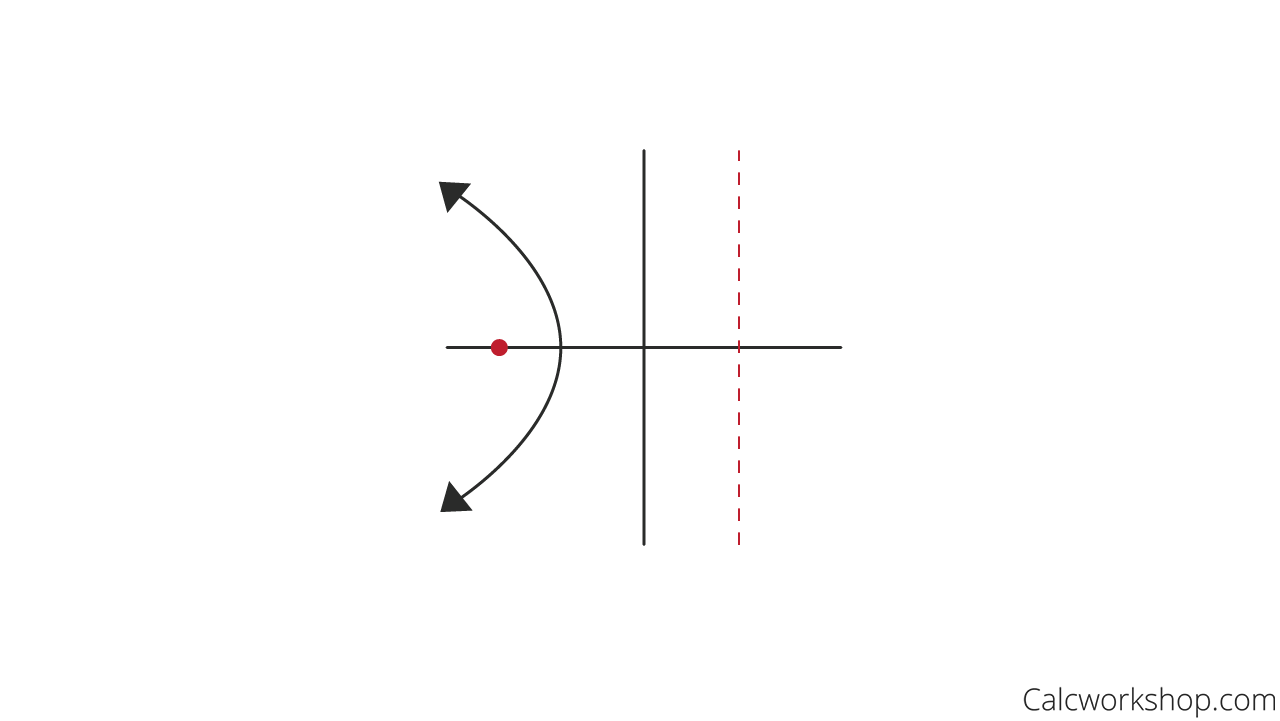
Graph of Parabola with Focus and Directrix
There’s a reason as to why a Parabola has symmetry, and that reason can be found by looking at it’s Focus and Directrix.
As Purple Math so eloquently states, the distance from any point on the parabola to its focus is always equal to the distance from that same point on the parabola to the directrix. Everything is balanced!
Well are the focus and directrix hard to find?
Nope!
The formula for finding all the major characteristics, or features, of a Parabola is very straightforward and easy to locate.
So, together we’re going to learn how to transform a Quadratic Equation into Graphing (h,k) Form and locate all the important components and create a beautiful graph!
Identifying Parabola Conics – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.