An important application of Exponential Functions is Compound Interest.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In order to really grasp the formula for Compound Interest, we first have to understand the terms:
- Principal Interest
- Compounding Interest
In the world of finance the term Principal is the initial deposit, loan or investment.
Whereas the concept of Compound Interest, according to The Calculator Site, is that interest is added back to the principal sum so that interest is earned on that added interest during the next compounding period.
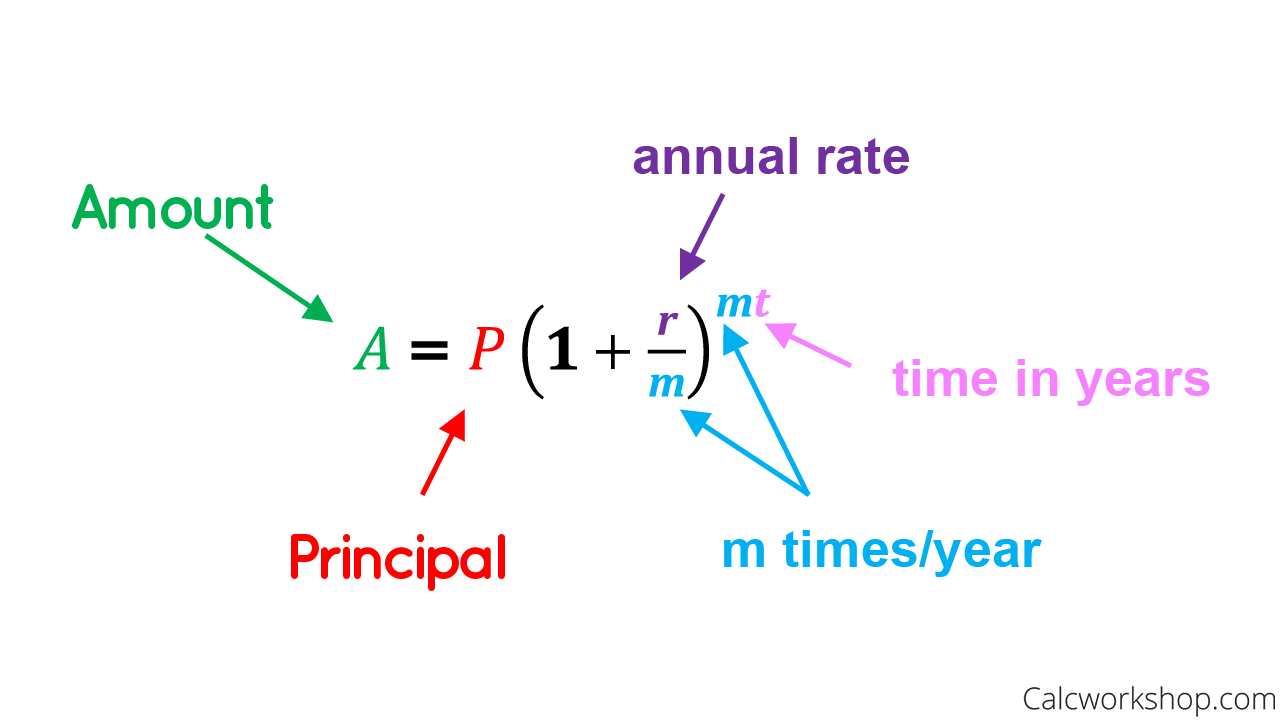
Compound Interest Formula
So all this means is that we put money in the bank in order to make more money via a good interest rate, and depending on how often the interest is compounded (i.e., annually, semiannually, quarterly, etc.) will determine how much money we make.
Together we will look at six classic examples, of how to figure out what is given and appropriately plug our values into our easy to use formula.
Then, we will discover where the irrational number e, perhaps the single most useful base for any exponential function, is derived.
Did you know that the number e occurs naturally when computing compound interest, and the letter e was chosen in honor of the mathematician, Leonhard Euler.
And in future lessons we will see how e can also be expressed as the sum of an infinite series as well as a limit expression. Cool!
Calculating Compound Interest – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.